
- •Введение
- •Лабораторная работа №1 общие приемы работы в среде ms excel
- •Методические указания Структура окна ms Excel.
- •Управление окнами и режимы отображения рабочих книг.
- •Перемещение по рабочей книге и выделение диапазонов ячеек.
- •Загрузка и сохранение документа.
- •Работа со справочной системой ms Excel.
- •Задания для выполнения работы Задание 1. Настройка оконного интерфейса ms Excel.
- •Задание 2. Выделение диапазонов ячеек.
- •Задание 3. Создание, редактирование и сохранение рабочей книги.
- •Задание 4. Работа со справочной системой ms Excel.
- •Контрольные вопросы
- •Лабораторная работа №2 Форматирование и рЕдактирование ячеек и таблиц
- •Методические указания
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №3 Числовые (пользовательские) форматы данных
- •Методические указания
- •Положит.Число; отрицат.Число; нуль; @ "текст".
- •Коды числовых форматов.
- •Коды цветов.
- •Коды условий.
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №4 Реализация арифметических и логических вычислений
- •Методические указания
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №5 Обработка Массивов в ms excel
- •Методические указания
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №6 Адресация в ms Excel
- •Методические указания
- •Абсолютная адресация:
- •Относительная адресация:
- •Смешанная адресация:
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №7 использование встроенных функций
- •Методические указания
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №8 Построение графиков и диаграмм
- •Методические указания
- •Редактирование диаграмм.
- •Применение диаграмм для анализа данных.
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №9 поиск решения средствами ms excel
- •Методические указания
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №10 Работа с базами данных
- •Методические указания Обработка списков данных. Основные понятия.
- •Рекомендации по организации списка.
- •Ввод данных в список.
- •Форматирование и сортировка списка.
- •Фильтрация списков.
- •Автоматическое подведение промежуточных итогов.
- •Сводная таблица.
- •Консолидация.
- •Задания для выполнения работы
- •Исходные данные
- •Контрольные вопросы
- •Лабораторная работа №11 основы программирования в среде vba
- •Методические указания Основные понятия языка vba.
- •Range("f2").Select ‘выделение ячейки f2
- •Редактор vba.
- •Правила задания имен объектов.
- •Типы данных vba.
- •Описание переменных.
- •Использование констант.
- •Организация ввода/вывода информации.
- •Задания для выполнения работы
- •Контрольные вопросы
- •Лабораторная работа №12 создание пользовательских функций средствами vba
- •Методические указания Создание пользовательских функций.
- •Основные операторы языка vba.
- •Задания для выполнения работы
- •Контрольные вопросы
- •Список использованной литературы
- •Приложение а Структура отчета
- •Приложение б Пример титульного листа
Задания для выполнения работы
1. Выполните задание в соответствии с вариантом (табл. 5.1).
Таблица 5.1
Исходные данные к выполнению задания 1
Вариант |
Задание |
|
|
Данные о доходах (тыс.ден.ед.) холдинговой компании по трем регионам трех компаний за 1998 и 2000 годы представлены в матрицах А и В:
По строкам группируются данные о доходах трех компаний, а по столбцам — по регионам продаж. Рассчитайте матрицу приростов доходов за период с 1998 по 2000 годы и матрицу, характеризующую средние размеры доходов компаний холдинга. |
|
|
Размер издержек перевозки товара (в ден.ед.), отгружаемого из трех заводов 4-м потребителям задан матрицей
Издержки производства на первом заводе равны 75, на втором — 42, на третьем — 54. Напишите матрицу Р издержек производства размером 3×4, элементы которой группируются по строкам и столбцам так же, как и в S. Определите матрицу совокупных издержек, объединяя затраты на производство и транспортирование товаров. |
|
|
Предприятие
производит продукцию трех видов и
использует сырье двух типов. Нормы
затрат сырья на единицу продукции
каждого вида заданы матрицей
|
Продолжение табл. 5.1 |
|
Вариант |
Задание |
|
|
Определите
затраты фирмы, производящей 80 единиц
продукции П1,
90 — продукции П2
и 130 — продукции П3,
если нормы затрат сырья на производство
единицы продукции каждого вида заданы
матрицей
Стоимость единицы
сырья каждого типа задана матрицей
|
|
|
Прибыль, полученная
от затрат сырья на единицу продукции
каждого вида некоторой фирмы, задана
матрицей
Определите прибыль фирмы, производящей изделия двух видов и использующей сырье двух типов, если фирма собирается производить 300 изделий первого вида и 250 — второго. |
|
|
Прибыль
фирмы после вычета налогов характеризуется
матрицей
Матрица
налогов для данной фирмы имеет вид
Определите матрицу прибыли фирмы до вычета налогов. |
|
|
Рабочие, менеджеры
имеют фиксированную зарплату,
выплачиваемую из прибыли фирмы.
Матрица совокупной прибыли имеет вид
Определите матрицу прибыли, с которой фирма может работать в следующем месяце.
|
Продолжение табл. 5.1 |
|
Вариант |
Задание |
|
|
На фирме работают 6 рабочих, которые производят продукцию.
Прибыль от продажи
продукции каждого рабочего описывается
матрицей
Матрица зарплаты
каждого рабочего
Фирма решает сократить штат рабочих до четырех человек. Кто из рабочих, скорее всего, будет уволен? |
|
|
То же условие, что и в задаче 8. Но фирма решает дать премию своему лучшему работнику. Кто из шести рабочих получит премию?
|
|
|
Возраст
каждого служащего фирмы представлен
матрицей
При возрастном ограничении на работу в фирме для мужчин 60 лет, для женщин — 55, определите, кто из нынешнего состава служащих будет работать и через 10 лет? |
|
|
Предприятие выпускает продукцию трех видов Р1, Р2, Р3 и использует сырье двух типов: S1 и S2.
Нормы расхода
сырья характеризуются матрицей где каждый элемент аij (i = 1, 2, 3; j = 1, 2) показывает, сколько единиц сырья j-го типа расходуется на производство единицы продукции i-го вида.
План
выпуска продукции задан матрицей-строкой
Определите затраты сырья, необходимые для планового выпуска продукции, и общую стоимость сырья. |
Окончание табл. 5.1 |
|
Вариант |
Задание |
|
|
Вычислить
|
2. Выполните задания в соответствии с вариантом (табл. 5.2).
Таблица 5.2
Исходные данные к выполнению задания 2
Вариант |
Задание |
|
|
Решите системы
линейных уравнений
|
Продолжение табл. 5.2 |
|
Вариант |
Задание |
|
|
Решите системы
линейных уравнений
,
|
|
|
Решите системы
линейных уравнений
,
|
|
|
Решите системы
линейных уравнений
,
|
|
|
Решите системы
линейных уравнений
,
|
Продолжение табл. 5.2 |
|
Вариант |
Задание |
|
|
Решите системы
линейных уравнений
,
и вычислить значение квадратичной
формы
|
|
|
Решите системы
линейных уравнений
,
и вычислить значение квадратичной
формы
|
|
|
Решите системы
линейных уравнений
,
|
|
|
Решите системы
линейных уравнений
,
, , .
|
Окончание табл. 5.2 |
|
Вариант |
Задание |
|
|
Решите системы
линейных уравнений
,
|
|
|
Решите системы линейных уравнений , и вычислить значение квадратичной формы , где
|
|
|
Решите системы линейных уравнений , и вычислить значение квадратичной формы , где
|

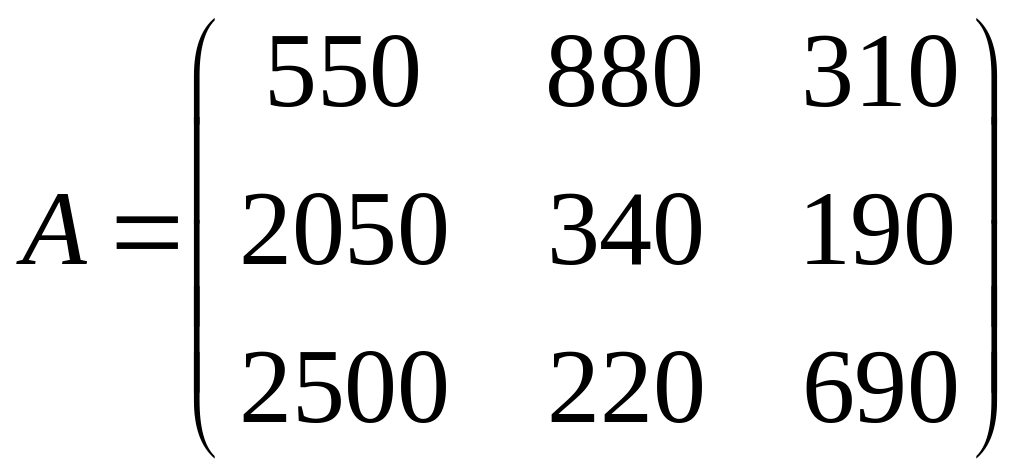
 .
. .
. .
Совокупную матрицу заработной платы
для всех служащих можно записать так
.
Совокупную матрицу заработной платы
для всех служащих можно записать так
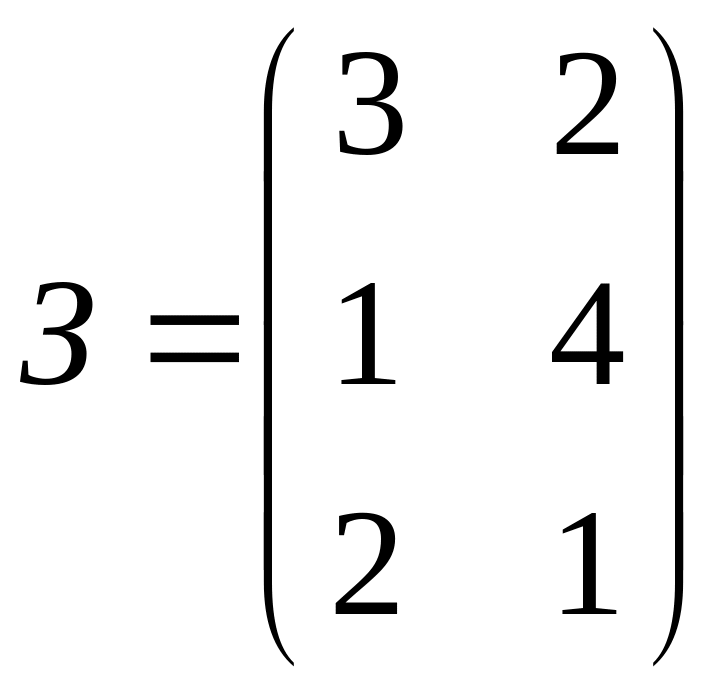 .
. .
Зарплата рабочих рассчитывается из
прибыли.
.
Зарплата рабочих рассчитывается из
прибыли.
 .
.
 ,
,
 ,
где
–
вектор из
,
где
–
вектор из
 ,
,
 ,
,
 ,
,

 ,
,
 ,
,
 .
. ,
,
 ,
,
 .
. ,
,
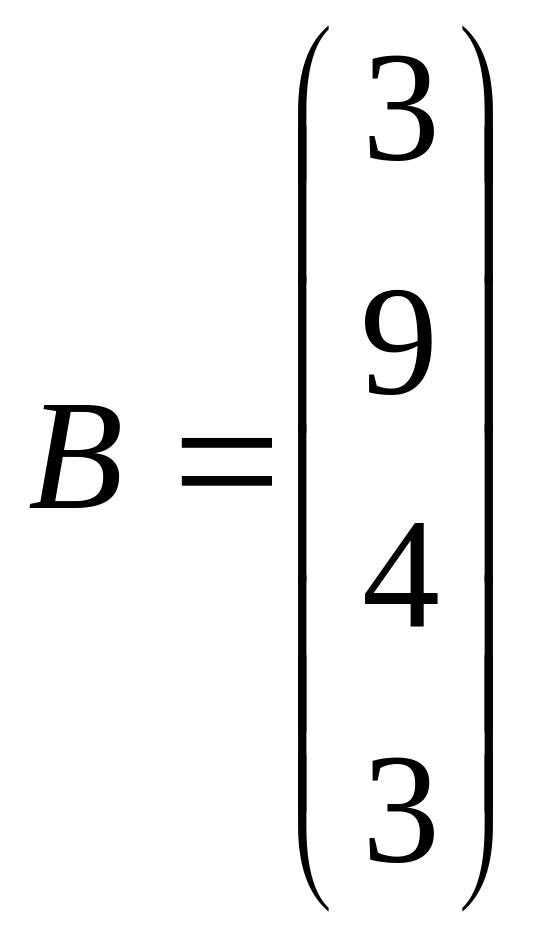 ,
,
 .
. ,
,
 ,
,
 .
. ,
,
 ,
,
 .
. ,
,
 ,
,
 .
. ,
,
 ,
,
 .
. ,
,
 ,
,
 .
. ,
,
 ,
,
 .
. ,
,
 ,
,
 .
.