2.3. Методичні вказівки до виконання лабораторної роботи Розв'язання задачі

Представимо таблицю з вихідними даними у наступному вигляді матриці відстаней (МВ):

i	j				hi
	1	2	3	4
1	Х	6	7	2	2
2	8	Х	6	9	6
3	5	8	Х	3	3
4	6	4	10	Х	4

Для одержання оцінки знизу довжин безлічі всіх гамільтонових контурів (ГК) скористаємося тим, що в кожний ГК входить тільки по одному елементі з кожного рядка й з кожного стовпця МВ. Тому якщо елементи будь-якого рядка або будь-якого стовпця зменшити на яке-небудь число, то на це ж число зменшаться довжини всіх ГК. На цій властивості заснований метод приведення МР. (ГК це замкнутий елементарний шлях, тобто елементарний контур, що проходить через всі населені пункти розглянутої задачі).

Приведення матриці може провадитися по рядках і по стовпцях. Приведення МВ по рядках укладається в тім, що з елементів кожного рядка i віднімається найменший елемент цього рядка, позначуваний h_i. При цьому довжини всіх ГК зменшаться на суму віднятих з кожного рядка чисел, тобто на величину , залишаючись у теж час ненегативними. Тому величина , рівна в нашім випадку 15, дає деяку оцінку знизу довжин всіх ГК. Отримана оцінка може бути поліпшена шляхом повторного приведення МВ по стовпцях. При цьому з елементів кожного стовпця j наведеної по рядках МВ віднімається найменший елемент цього стовпця, позначуваний g_j . Сума віднятих при цьому чисел Уточнена оцінка знизу довжин ГК

Одержувана після приведення МВ дана у вигляді наступної таблиці:

i	j
	1	2	3	4
1	Х	4	5	0
2	0	Х	0	3
3	0	5	Х	0
4	0	0	6	Х

Метод приведення МВ будемо застосовувати й далі для одержання оцінок знизу різних підмножин множини ГК.

Розглянемо тепер спосіб розбивки множини ГК на підмножини. Візьмемо деяку дугу (i , j). До першої підмножини віднесемо всі ГК, у які ця дуга входить. Позначимо цю підмножину [(i , j)]. До другої підмножини віднесемо всі ГК, у які дуга (i , j) не входить. Цю підмножину позначимо .

МВ для підмножини [(i , j)] легко одержати, якщо врахувати, що включення дуги (i , j) у ГК виключає можливість включення інших дуг, що коштують в i-ом рядку або j-ом стовпці. Отже, МВ для підмножини [(i , j)] виходить із первісної таблиці викреслюванням i-ого рядка й j-ого стовпця.

Для того, щоб одержати МВ для підмножини , треба в первісній таблиці заборонити рух по дузі (i , j), поклавши її довжину рівної нескінченності. Ця заборона руху по дузі (i , j) будемо відзначати хрестом у відповідній клітці первісної таблиці.

Тепер виникає питання: яку дугу покласти в основу розбивки множіни ГК на відповідні підмножини ?

Якщо як дуга (i , j) взяти таку, у якої в наведеній таблиці , то для групи оцінка знизу зросте на d_i,j, оскільки заздалегідь відомо, що ця дуга ввійде в усі ГК. Вона може ще зрости, якщо таблиця при викреслюванні i-ого рядка й j-ого стовпця буде допускати подальше приведення. У той же час при заміні елемента d_i,j на нескінченність МВ залишиться наведеної, тобто оцінка знизу для не зросте. Отже, менше значення оцінки знизу буде для підмножини , що не бажано. Тому як дуга (i , j) треба брати таку, у якої в наведеної МВ величина

Але таких дуг трохи. Яку ж з них вибрати ? Очевидно, ту, для якої збільшення оцінки для підмножини буде найбільшим, тому що при цьому вийде найбільша різниця в оцінках для підмножин [(i , j)] і .

Позначимо збільшення оцінки підмножини через Значення цієї величини одержуємо шляхом додавання найменших чисел i-ого рядка й j-ого стовпця.

Знову звернемося до нашого приклада. Для наведеної МВ значення виходять рівними:

Найбільше збільшення оцінки для групи виходить для дуги (2, 3). Виключаємо другий рядок й третий стовпець з наведеної МВ, приходимо до таблиці, що представляє собою МВ для підмножини [(2, 3)]:

i	j
	1	2	4
1	Х	4	0
3	0	X	0
4	0	0	Х

При одержанні подібних матриць потрібно строго стежити за тим, щоб не могло вийти контурів, що не є ГК. Оскільки дуга (2, 3) уже уведена в намічений ГК, то в останній таблиці потрібно накласти заборона на дугу (3, 2), відзначивши еее хрестиком, тому що дуга (3, 2) разом з дугою (2, 3) утворить контур.

Нижче представлена наведена МВ зі збільшенням оцінки

i	j
	1	2	4
1	Х	4	0
3	0	X	0
4	0	0	Х

Для неї величини рівні

Найбільше збільшення оцінки для групи виходять для дуг (1, 4) і (4, 2), які також уводимо в намічуваний ГК, одержуючи ланцюжок (1, 4, 2, 3), для замикання якого не вистачає лише дуги (3, 1).

Отже, подальші перетворення не доречні й отриманий ГК є оптимальним з величиною шляху 17: 2 4 6 5

= 17.

Спробуємо звести цю задачу до задачі цілочисельного лінійного програмування. Для цього сукупність дуг ГК можна описати у вигляді наступної матриці

у котрій

А тому що кожна вершина зустрічається в ГК лише один раз, що означає наявність у кожному рядку й у кожному стовпці матриці Y тільки однієї одиниці. Математично це запишеться у наступному виді

Виходячи з того, що всі y_ij можуть приймати значення 0 або 1, можна замінити вимогою, щоб всі y_ij були ненегативними цілими числами

Як бачимо, кожний ГК можна представити у вигляді матриці Y, елементи котрої y_ij задовольняють вищенаведеним співвідношенням. При этом длина ГК, яка дорівнює суме довжин складових його дуг, найдётся по формуле

де d_ij – величина відстані від i-го населеного пункту до j-ого.

У такий спосіб знаходження оптимального ГК мінімальної довжинизводиться до знаходження значень змінних y_ij, що задовольняють наведеним вище лінійним рівностям і нерівностям, умові цілочисельності й обертаючих у максимум лінійну форму L, тобто до рішення задачі цілого чисельного лінійного програмування.

Нижче наведений результат розв'язання поставленої задачі за допомогою функції “Пошук рішення” табличного процесора EXCEL (рис. 2.1).

У верхній частині рис. 2.1 наведена таблиця з вихідними даними, а в нижній його частині – сам результат рішення, що означає послідовне переміщення комівояжера:

• з першого міста у четверте (клітка F10);

• потім з четвертого міста у друге (клітка D13);

• потім з другого міста у третє (клітка E11);

• і в конце з третього міста у перше (клітка C12).

Сумарна мінімальна довжина оптимального ГК становить 17 одиниць відстані (див. клітку цільової функції В15).

При цьому клітки з G10 по G13 містять суми розташованих ліворуч чотирьох кліток, а клітки із С14 по F14 - суми розташованих вище чотирьох кліток і в клітках із С15 по F15 полічені мінімальні відстані дуг ГК. Зокрема для клітки С15 це опишеться наступною формулою - С3*С10+С4*С11+С5*С12+С6*С13.

Клітка із цільовою функцією В15 містить суму чотирьох кліток розташованих праворуч від її, що означає сумарну мінімальну довжину ГК.

Рис. 2.1. Результат розв'язання поставленої задачі за допомогою функції “Пошук рішення” табличного процесора EXCEL

На рис. 2.2 наведене діалогове вікно функції “Пошук рішення” табличного процесора EXCEL, де описані:

• цільова клітка В15;

• напрямок оптимізації - мінімізація;

• діапазон змінюваних кліток - C10:F13;

• обмеження задачі, які задані у вигляді однієї нерівності (C10:F1# >= 0) і двох рівностей (C7:F7 = C14:F14 і G3:G6 = G10:G13).

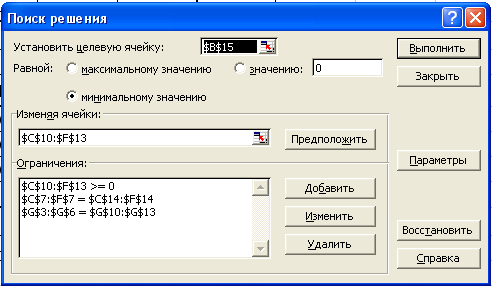
Рис. 2.2. Діалогове вікно функції “Пошук рішення” табличного процесора EXCEL