
- •Министерство образования и науки украины донецкий национальный университет
- •По теории статистики
- •Скоробогатова Нелля Вікторівна
- •(Російською мовою)
- •Тема 1. Статистическое наблюдение Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 2. Сводка и группировка данных Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 3. Графический метод Методические указания
- •Беларусь
- •10. Что такое графический образ?
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 5. Анализ рядов распределения. СтаТиСтическая проверка гипотез Методические указания
- •Решение типовых задач
- •Решение
- •Распределение студентов по успеваемости
- •Решение
- •Решение
- •Кумулятивные показатели распределения семей по среднедушевому доходу
- •Вспомогательная таблица для расчета теоретических частот нормального распределения
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 6. Выборочное наблюдение Методические указания
- •Формулы необходимого объема выборки для различных способов формирования выборочной совокупности выводятся из соответствующих соотношений, используются при расчете предельных ошибок выборки.
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 7. Анализ интенсивности динамики Методические указания
- •Формулы показателей анализа ряда динамики
- •1. Что характеризует уровень ряда динамики?
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 8. Анализ тенденций развития Методические указания
- •Уравнения, используемые при аналитическом выравнивании динамических рядов
- •Решение типовых задач
- •Решение
- •Вспомогательные расчеты для определения параметров а0 и а1 уравнения прямой и критерия статистической точности аналитического уравнения
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 9. Индексы Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Тема 10. Статистические методы изучения
- •ВзаимОсвязей социально-экономических
- •Явлений
- •Методические указания
- •Шкала Чеддока
- •На основе данных аналитической группировки строится график эмпирической линии связи, вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о ее форме.
- •Системы нормальных уравнений для разных форм связи
- •3) Рассчитывается коэффициент ранговой корреляции Спирмена ( ): ;
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Вспомогательная таблица для расчета параметров уравнения связи
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Ответы на тестовые задания
- •Ответы к задачам
- •Тема 10
Решение типовых задач
Пример 1. По итогам аналитической группировки, изучающей зависимость средней заработной платы рабочих от возраста (пример 6 темы 5) с помощью однофакторного дисперсионного анализа: 1) проерить статистическую существенность зависимости; 2) оценить тесноту связи между средней заработной платой и возрастом.
Решение
1. Для проверки статистической существенности зависимости между изучаемыми факторами строим однофакторный дисперсионный комплекс (табл.10.6), предварительно рассчитав соответствующие девиации и дисперсии:


+![]()
![]()
![]()
![]()
![]()

= 269000.
Таким образом, выполняется правило разложения вариации:
![]() ,
или 269000 = 234000 + 3500.
,
или 269000 = 234000 + 3500.
Определяем
число степеней свободы для каждого вида
девиации:
![]()
![]()
![]() .
.
Тогда соответствующие дисперсии будут равны:
факторная: ;
остаточная:
;
остаточная: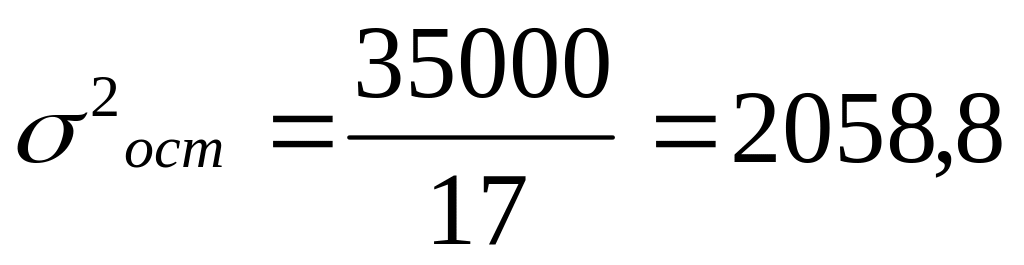 ;
;
общая:
 .
.
По
соотношению
![]() рассчитывается F-
критерий:
рассчитывается F-
критерий:
 Итоговые
значения рассчитанных характеристик
представим в таблице 10.6.
Итоговые
значения рассчитанных характеристик
представим в таблице 10.6.
Таблица 10.6
Однофакторный дисперсионный комплекс зависимости средней заработной платы от возраста рабочих
Источник вариации |
Девиа ция |
Число степе- ней свободы |
Дисперсия |
F – кри-терий |
Между группами |
234000 |
|
факторная
|
=56,83 |
Внутри групп |
35000 |
|
остаточная
или случайная
|
|
Общая |
269000 |
|
общая
|
Табличное
значение F–критерия: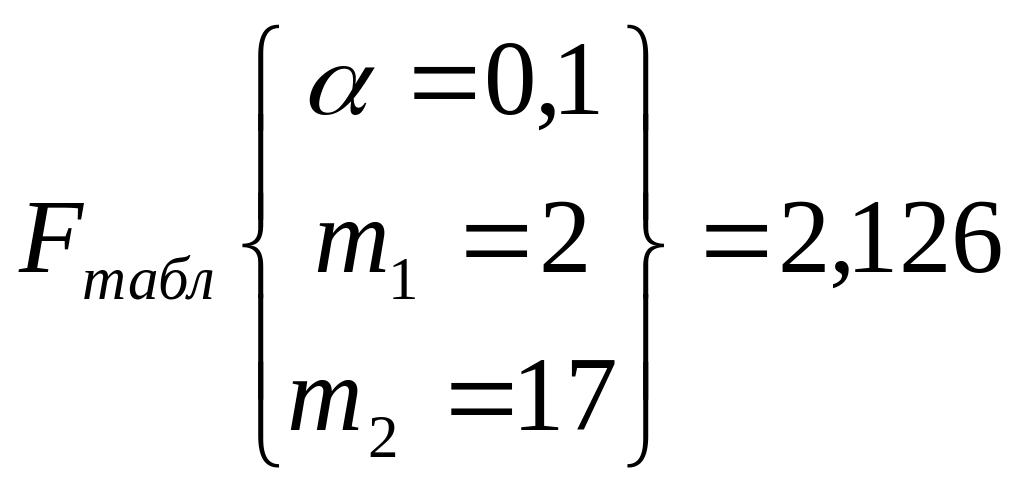 (приложение
2);
(приложение
2);
![]() >
>![]() поэтому
зависимость между средней заработной
платой и возрастом является существенной
или статистически значимой.
поэтому
зависимость между средней заработной
платой и возрастом является существенной
или статистически значимой.
2.
Рассчитываем эмпирическое корреляционное
отношение (![]() ):
):
 .
.
где![]() ;
;![]() (итоги решения прим. 6 в теме 5)
(итоги решения прим. 6 в теме 5)
При
подтверждении статистической зависимости
для оценки тесноты связи рассчитываем
коэффициент детерминации (![]() ):
):
 .
.
Зависимость между возрастом рабочих и средней месячной заработной платой очень тесная - на 87 % изменение зарплаты обусловлено возрастом рабочих.
Пример 2. По 12-ти предприятиям имеются следующие данные о годовой производительности труда работника (тыс.грн) и вооруженности труда основным капиталом (тыс.грн/чел.) (таблица 10.7).
На основании приведенных данных: 1) оцените тесноту связи между показателями с помощью коэффициента Фехнера и коэффициента ранговой корреляции Спирмена; 2) выявите зависимость и тесноту связи между показателями с помощью парного корреляционно-регрессионного анализа. Сделайте выводы.
Решение
1. Для определения коэффициента Фехнера рассчитываем средние значения признаков:
 тыс.грн/чел,
тыс.грн/чел,
 тыс.грн.
тыс.грн.
Определяем
знаки отклонений от среднего, т.е. знаки
![]() и
и
![]() и
заносим в таблицу 10.6 (гр.3 и 4), а затем
подсчитываем число совпадений и
несовпадений знаков отклонений (гр.5).
Тогда:
и
заносим в таблицу 10.6 (гр.3 и 4), а затем
подсчитываем число совпадений и
несовпадений знаков отклонений (гр.5).
Тогда:
 .
Коэффициент, равный 0,5 свидетельствует
о наличии прямой и умеренной зависимости
между производительностью труда и
капиталовооруженностью труда.
.
Коэффициент, равный 0,5 свидетельствует
о наличии прямой и умеренной зависимости
между производительностью труда и
капиталовооруженностью труда.
Для
определения коэффициента ранговой
корреляции (
)
проранжируем в порядке возрастания
факторный и результативный признаки,
т.е. определяем Rх
и
Rу
и занесем их в гр.6 и 7 таблицы 10.7. Затем
рассчитываем
![]() и заносим в гр.8 данной таблицы. Тогда
коэффициент ранговой корреляции Спирмена
будет равен:
и заносим в гр.8 данной таблицы. Тогда
коэффициент ранговой корреляции Спирмена
будет равен:
 .
.
Теснота связи между анализируемыми показателями прямая и достаточно тесная.
2. На первом этапе применения методики парного корреляционного анализа проверяем, выполняются ли требования, предъявляемые к факторному и результативному признакам.
-
Однородность распределений. Все
промежуточные расчеты представлены в
таблице 10.8.


 ;
;
 ;
;
 ;
;

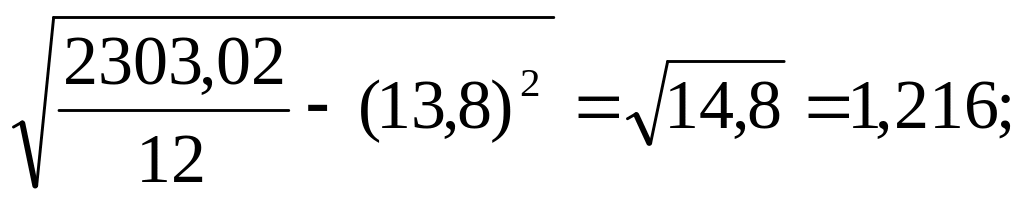
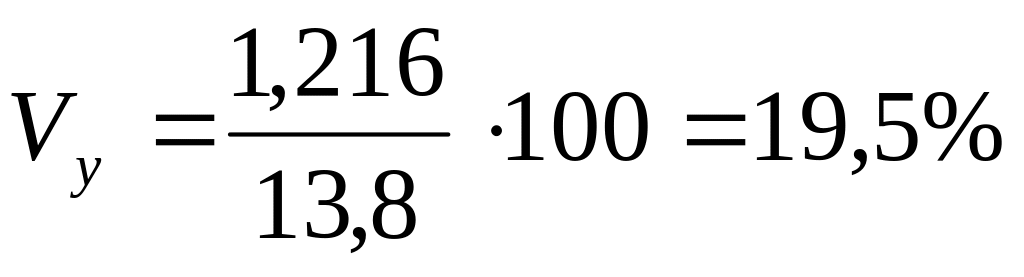
Коэффициенты
вариации (![]() и
и
![]() )
меньше 33%, что подтверждает гипотезу о
статистической однородности и
капиталовооруженности труда и
производительности труда.
)
меньше 33%, что подтверждает гипотезу о
статистической однородности и
капиталовооруженности труда и
производительности труда.
- Соответствие нормальному закону распределения.
По правилу “трех сигм” определяем интервалы:
а)
для факторного признака
![]() ;
;![]() или
или![]()
![]() ;
хmin=298;
хmax=366;
отсюда 298 и 366 є
;
хmin=298;
хmax=366;
отсюда 298 и 366 є
![]() ,
т.е. с вероятностью 0,997 можно утверждать,
что факторный признак соответствует
нормальному закону распределения;
,
т.е. с вероятностью 0,997 можно утверждать,
что факторный признак соответствует
нормальному закону распределения;
б)
для результативного признака
![]() ;
;
![]() или
или
![]() ;
уmin=12,5;
уmax=16,3.
Тогда:12,5 и 16,3 є
.
;
уmin=12,5;
уmax=16,3.
Тогда:12,5 и 16,3 є
.
Значит, с той же вероятностью и результативный признак соответствует нормальному закону распределения.
- Требования, связанные с независимостью по объектам наблюдения и взаимнооднозначном соответствии факторного и результативного признака, подтверждаются на этапе постановки задачи с помощью содержательного анализа исходной информации.
Следующая задача в методике парного корреляционно-регрес-сионного анализа – выбор формы связи между признаками. Для этого строим корреляционное поле (рис.10.1).
По
расположению точек на корреляционном
поле выбираем линейную форму связи,
т.е. уравнение связи будет следующее:
![]() .
.
Таблица 10.7
Расчетная таблица для определения непараметрических показателей тесноты связи
№ предприятия |
Капиталовооруженность труда, тыс. грн/чел, х |
Годовая производительность труда, тыс. грн., у |
Знак отклонения от среднего
|
Число совпадений (несовпадений) знаков |
Ранги |
|
||
факторного признака |
результативного признака |
по х Rx |
по у Rу |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
360,0 |
15,2 |
+ |
+ |
С |
10 |
10 |
0 |
2 |
298,0 |
12,8 |
- |
- |
С |
1 |
3 |
4 |
3 |
328,0 |
13,8 |
- |
0 |
Н |
6 |
8 |
4 |
4 |
330,0 |
14,0 |
0 |
+ |
С |
7 |
9 |
4 |
5 |
366,0 |
16,3 |
+ |
+ |
С |
12 |
12 |
0 |
6 |
316,0 |
12,6 |
- |
- |
С |
4 |
2 |
4 |
7 |
334,0 |
13,2 |
+ |
- |
Н |
9 |
6 |
9 |
8 |
300,0 |
12,9 |
- |
- |
С |
2 |
4 |
4 |
9 |
314,0 |
13,1 |
- |
- |
С |
3 |
5 |
4 |
10 |
320,0 |
12,5 |
- |
- |
С |
5 |
1 |
16 |
11 |
362,0 |
15,7 |
+ |
+ |
С |
11 |
11 |
0 |
12 |
332,0 |
13,5 |
+ |
- |
Н |
8 |
7 |
1 |
Всего |
3960,0 |
165,6 |
|
|
|
|
|
59 |
Таблица 10.8
Вспомогательные расчеты характеристик для парного корреляционно-регрессионного анализа
№ п/п |
х |
у |
х2 |
у2 |
ху |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
360,0 |
15,2 |
129600 |
231,04 |
5472 |
15,3 |
1,96 |
0,01 |
900 |
0,0066 |
2 |
298,0 |
12,8 |
88804 |
163,84 |
3814,4 |
12,2 |
1,0 |
0,36 |
1024 |
0,047 |
3 |
328,0 |
13,8 |
107584 |
190,44 |
4526,4 |
13,7 |
0 |
0,01 |
4 |
0,0072 |
4 |
330,0 |
14,0 |
108900 |
196 |
4620 |
13,8 |
0,04 |
0,04 |
0 |
0,0143 |
5 |
366,0 |
16,3 |
133956 |
265,69 |
5965,8 |
15,6 |
6,25 |
0,49 |
1296 |
0,043 |
6 |
316,0 |
12,6 |
99856 |
158,76 |
3981,6 |
13,1 |
1,44 |
0,25 |
196 |
0,04 |
7 |
334,0 |
13,2 |
111556 |
174,24 |
4408,8 |
14,0 |
0,36 |
0,64 |
16 |
0,134 |
8 |
300,0 |
12,9 |
90000 |
166,41 |
3870 |
12,3 |
0,81 |
0,36 |
900 |
0,0465 |
9 |
314,0 |
13,1 |
98596 |
171,61 |
4113,4 |
13,0 |
0,49 |
0,01 |
256 |
0,0076 |
10 |
320,0 |
12,5 |
102400 |
156,25 |
4000 |
13,3 |
1,69 |
0,64 |
100 |
0,064 |
11 |
362,0 |
15,7 |
131044 |
246,49 |
5683,4 |
15,4 |
3,61 |
0,09 |
1024 |
0,019 |
12 |
332,0 |
13,5 |
110224 |
182,25 |
4482 |
13,5 |
0,09 |
0 |
4 |
0 |
Всего |
3960,0 |
165,6 |
1312520 |
2303,02 |
54937,8 |
|
17,74 |
2,9 |
5720 |
0,4292 |

•
•
•
•
•
• •
•
•
• •
• •

……. - корреляционное поле;
- теоретическая линия регрессии.
Рис. 10.1. Корреляционное поле и теоретическая линия регрессии.
Определяем параметры а0 и а1 по упрощенным формулам, т.е.

 .
.
где
 ;
;
![]() ;
;
![]() ;
;
![]()
Линейное
уравнение связи будет иметь следующий
вид:![]()
Параметр а1 = 0,05 показывает, что годовая производительность труда в среднем возрастет на 0,05 тыс.грн., если капиталовооруженность труда увеличится на одну тыс.грн., т.е. прирост капиталовооруженности на одну тыс. грн. сопровождается ростом производительности труда в среднем на 0,05 тыс.грн., а0 не имеет содержательной интерпретации.
Следующая задача – определение показателей тесноты связи. Рассчитываем:
-
парный коэффициент корреляции:
 ;
;
-
парный коэффициент детерминации:
![]() ;
;
коэффициент
эластичности:

Зависимость
между капиталовооруженностью труда и
годовой производительностью труда
сложилась прямая (![]() )
и достаточно тесная, в среднем на 83,0%,
колеблемость (или изменение)
производительности труда вызывается
изменением капиталовооруженности
труда. При этом каждый процент прироста
капиталовооруженности труда сопровождается
приростом производительности труда на
1,2%.
)
и достаточно тесная, в среднем на 83,0%,
колеблемость (или изменение)
производительности труда вызывается
изменением капиталовооруженности
труда. При этом каждый процент прироста
капиталовооруженности труда сопровождается
приростом производительности труда на
1,2%.
Следующая задача – проверка статистической значимости характеристик парного корреляционно-регрессионного анализа и статистической точности уравнения связи:
- парного коэффициента корреляции - на основе t-критерия (приложение 1):
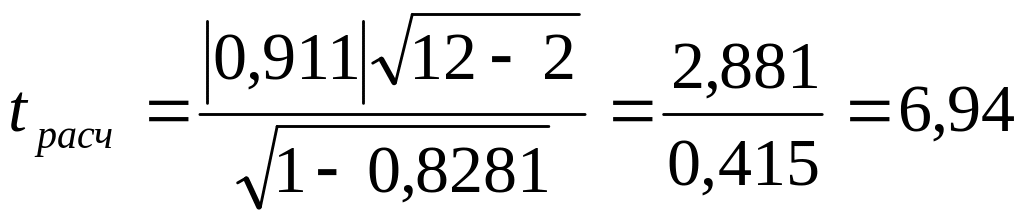 ;
tтеор
;
tтеор 2,228; tрасч>tтабл.
2,228; tрасч>tтабл.
С вероятностью 0,95 можно утверждать, что парный коэффициент корреляции статистически значимый или достоверный.
- уравнения связи - на основе F-критерия:

(расчет
![]() и
и
![]() представлен
в гр.7 и 8 табл.10.8)
представлен
в гр.7 и 8 табл.10.8)
 ,
т.е. Fрасч
> Fтабл
(приложение
2).С вероятностью 0,95 можно утверждать,
что линейное уравнение связи статистически
достоверно.
,
т.е. Fрасч
> Fтабл
(приложение
2).С вероятностью 0,95 можно утверждать,
что линейное уравнение связи статистически
достоверно.
- параметров уравнения связи - на основе t–критерия:
 ;
;
![]() ;
;
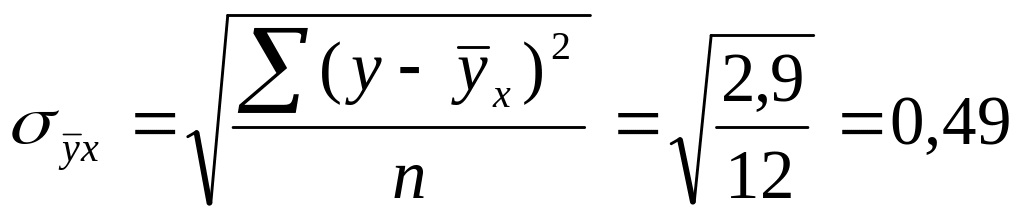 ;
;
 ;
;
 ;
;
 ;
;
![]() ;
;
![]() ,
т.е. параметры уравнения связи являются
статистически достоверными или надежными.
Для проверки статистической точности
уравнения связи рассчитываем относительную
ошибку аппроксимации (гр.10, табл.10.8)
,
т.е. параметры уравнения связи являются
статистически достоверными или надежными.
Для проверки статистической точности
уравнения связи рассчитываем относительную
ошибку аппроксимации (гр.10, табл.10.8)
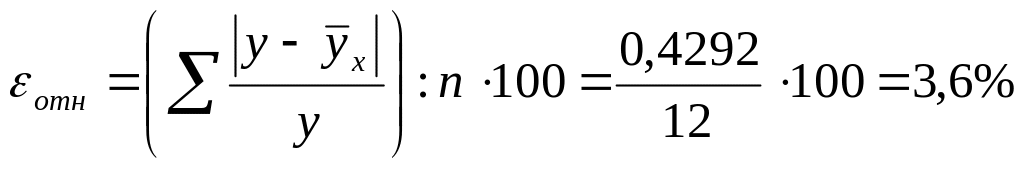 ,
,![]() ,
что подтверждает статистическую точность
полученного уравнения регрессии.
,
что подтверждает статистическую точность
полученного уравнения регрессии.
Пример 3. Известны следующие данные о валовом доходе и оборотных средствах торгового предприятия по кварталам 2001 и 2002гг.
Кварталы |
Стоимость оборотных средств, тыс.грн. |
Валовой доход, тыс.грн. |
2001 год |
||
1 |
50,0 |
63,0 |
П |
56,0 |
70,0 |
Ш |
35,0 |
48,0 |
1V |
36,0 |
50,0 |
2002 год |
||
1 |
40,0 |
60,0 |
П |
45,0 |
54,0 |
Ш |
42,0 |
70,0 |
1V |
48,0 |
65,0 |
Выявите зависимость между валовым доходом и стоимостью оборотных средств с помощью методики корреляционно-регрессион-ного анализа. Обоснуйте выбор размерности уравнения связи и способа его расчета. Сделайте выводы.


