
- •Министерство образования и науки украины донецкий национальный университет
- •По теории статистики
- •Скоробогатова Нелля Вікторівна
- •(Російською мовою)
- •Тема 1. Статистическое наблюдение Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 2. Сводка и группировка данных Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 3. Графический метод Методические указания
- •Беларусь
- •10. Что такое графический образ?
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 5. Анализ рядов распределения. СтаТиСтическая проверка гипотез Методические указания
- •Решение типовых задач
- •Решение
- •Распределение студентов по успеваемости
- •Решение
- •Решение
- •Кумулятивные показатели распределения семей по среднедушевому доходу
- •Вспомогательная таблица для расчета теоретических частот нормального распределения
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 6. Выборочное наблюдение Методические указания
- •Формулы необходимого объема выборки для различных способов формирования выборочной совокупности выводятся из соответствующих соотношений, используются при расчете предельных ошибок выборки.
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 7. Анализ интенсивности динамики Методические указания
- •Формулы показателей анализа ряда динамики
- •1. Что характеризует уровень ряда динамики?
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 8. Анализ тенденций развития Методические указания
- •Уравнения, используемые при аналитическом выравнивании динамических рядов
- •Решение типовых задач
- •Решение
- •Вспомогательные расчеты для определения параметров а0 и а1 уравнения прямой и критерия статистической точности аналитического уравнения
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 9. Индексы Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Тема 10. Статистические методы изучения
- •ВзаимОсвязей социально-экономических
- •Явлений
- •Методические указания
- •Шкала Чеддока
- •На основе данных аналитической группировки строится график эмпирической линии связи, вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о ее форме.
- •Системы нормальных уравнений для разных форм связи
- •3) Рассчитывается коэффициент ранговой корреляции Спирмена ( ): ;
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Вспомогательная таблица для расчета параметров уравнения связи
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Ответы на тестовые задания
- •Ответы к задачам
- •Тема 10
3) Рассчитывается коэффициент ранговой корреляции Спирмена ( ): ;
4) оценивается статистическая достоверность коэффициента с помощью t–критерия, аналогично для парного коэффициента корреляции.
Для определения тесноты связи между произвольным числом ранжированных признаков рассчитывается множественный коэффициент ранговой корреляции или коэффициент конкордации (W) по следующей формуле:
для несвязных
рангов:
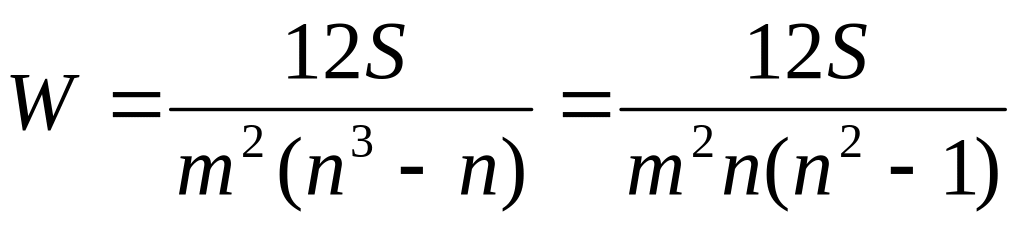 ,
,
где m
- число факторов; S
- отклонение
суммы квадратов рангов от средней
квадратов рангов; n
- число наблюдений;
![]()
для связных рангов:
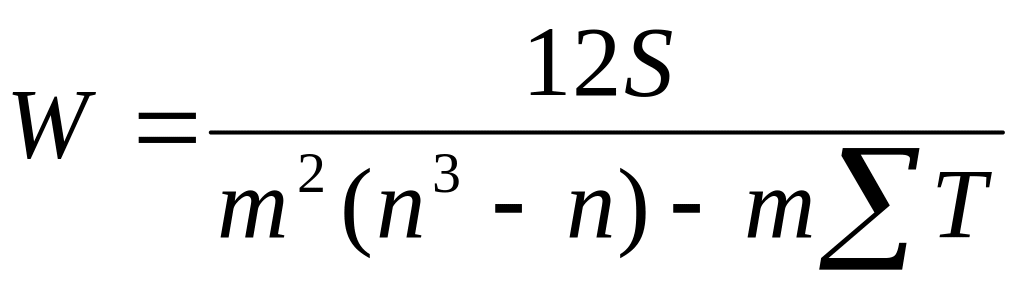 ,
,
где
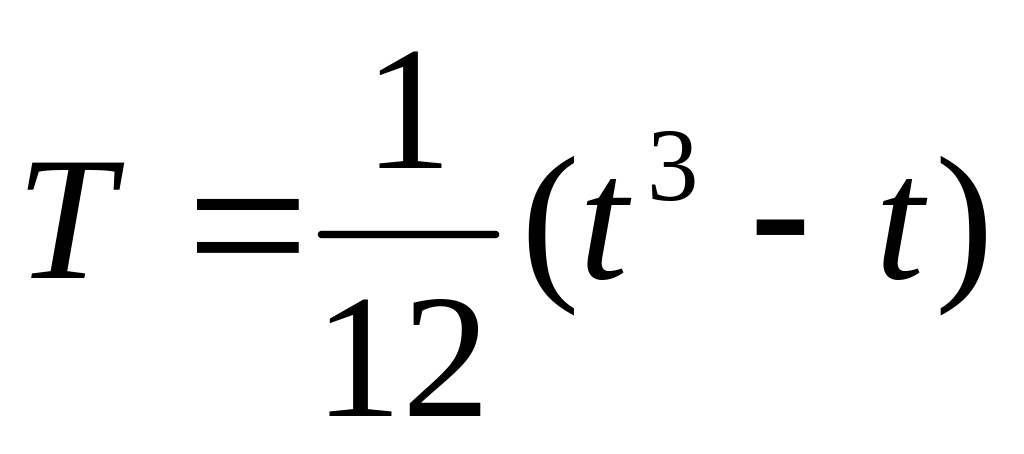 ,
а t - количество связнных рангов по
определенным показателям.
,
а t - количество связнных рангов по
определенным показателям.
Значимость
коэффициента проверяется на основе
![]() -
критерия Пирсона:
-
критерия Пирсона:
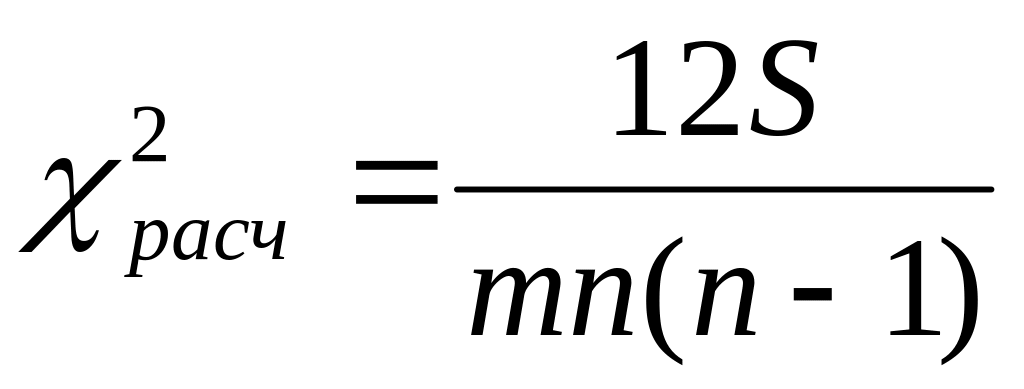 ;
;
![]() определяется
по заданному уровню вероятности (р)
и числе степеней свободы:
определяется
по заданному уровню вероятности (р)
и числе степеней свободы:
![]() ,
при условии
,
при условии
![]() >
коэффициент конкордации является
статистически достоверным (приложение
4).
>
коэффициент конкордации является
статистически достоверным (приложение
4).
Оценка тесноты связи между альтернативными и атрибутивными признаками. Оценка тесноты связи между альтернативными признаками осуществляется на основе тетрахорических таблиц или таблиц взаимной сопряженности (табл. 10.4)
На основе таблицы сопряженности рассчитывается коэффициенты:
-
ассоциация (![]() ):
):
![]() ;
;
контингенции(![]() ):
):
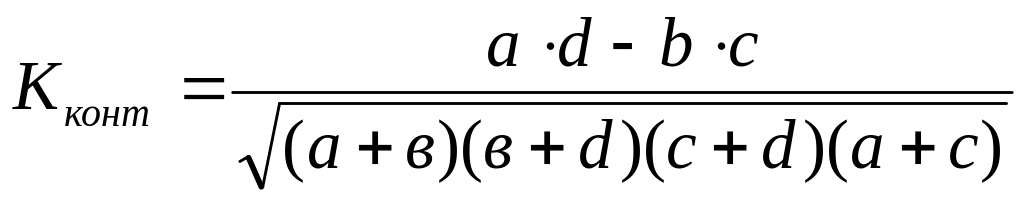 .
.
Они
меняются в пределах от - 1 до + 1 и всегда
![]() <
<
![]() .
.
Связи считаются подтвержденными, если ≥ 0,5 и ≥ 0,3.
Таблица 10.4
Распределение частот по сочетанию альтернативных признаков
Факторный признак |
Результативный признак |
Итого |
|
наличие |
отсутствие |
||
наличие |
а |
в |
а + в |
отсутствие |
с |
d |
в + d |
Итого |
а + с |
в + d |
n |
где а, в, с, d - частота взаимного сочетания соответствующих альтернатив, n - общая сумма частот.
Если факторный и результативный признак имеют разновидностей больше 2-х, т.е. являются атрибутивными, то для оценки тесноты связей между ними применяются: коэффициент взаимной сопряженности К. Пирсона (С) и коэффициент взаимной сопряженности А.А. Чупрова (Т ).
Для их определения первичная статистическая информация представляется в форме таблицы сопряженности (табл.10.5).
Коэффициент взаимной сопряженности К. Пирсона определяется по формуле:
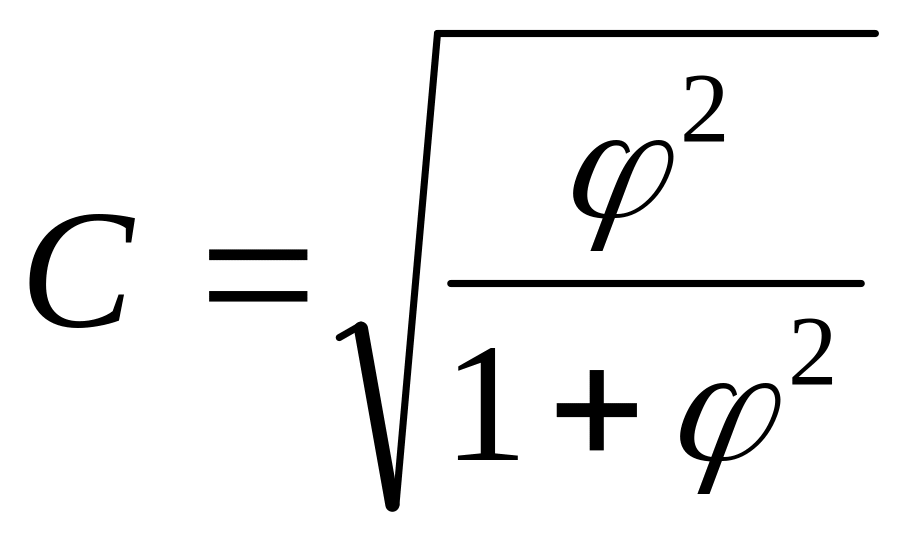 ,
где
,
где
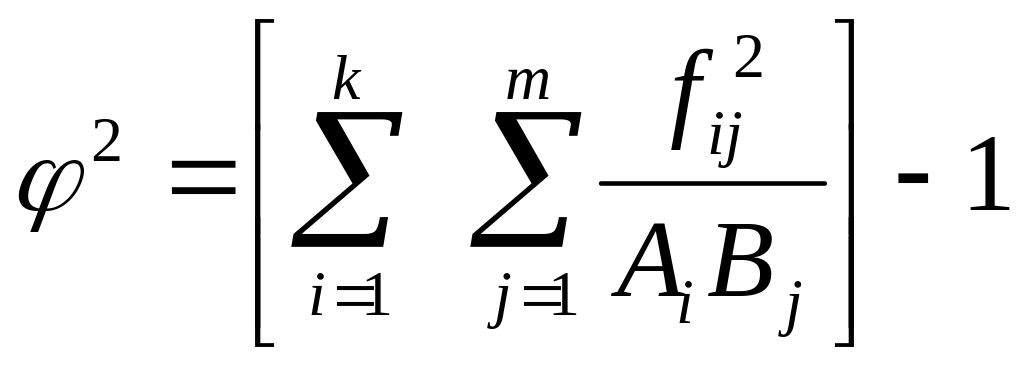 .
.
Коэффициент взаимной сопряженности А.А. Чупрова рассчитывается так:
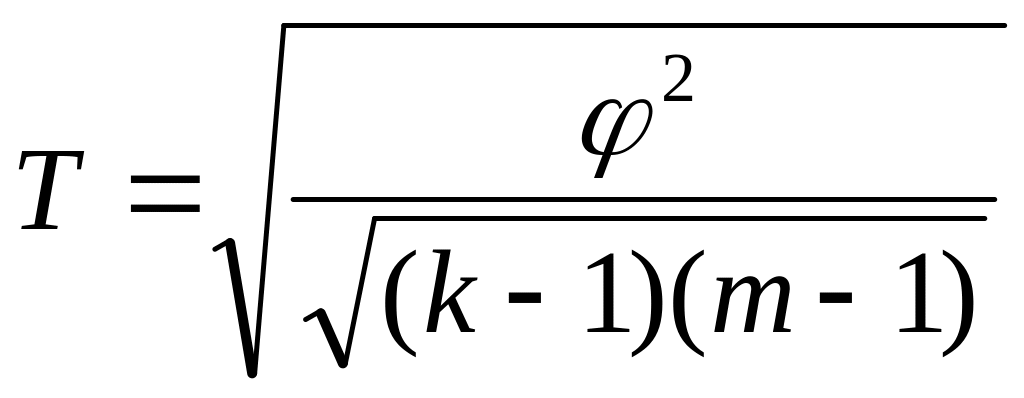 .
.
Таблица 10.5
Таблица сопряженности между атрибутивными признаками
Группы по фактор ному признаку |
Группы по результативному признаку |
Итого |
|||
В1 |
В2 |
… |
В m |
||
А1 |
f11 |
f12 |
… |
f1 m |
А1 |
А2 |
f21 |
f22 |
… |
F2 m |
А2 |
… |
… |
… |
… |
… |
… |
Аk |
fk 1 |
fk 2 |
… |
fk m |
Аk |
Итого |
В1 |
В2 |
… |
В m |
n |
где
![]() -
частоты взаимного соответствия двух
атрибутивных признаков, i - номер
группы факторного признака,
-
частоты взаимного соответствия двух
атрибутивных признаков, i - номер
группы факторного признака,
![]() ,
k - число разновидностей факторного
признака,
-
номер группы результативного признака;
,
k - число разновидностей факторного
признака,
-
номер группы результативного признака;
![]() ,
m - число разновидностей результативного
признака; Аi - итоговые
частоты по строкам; Вj -
итоговые частоты по столбцам.
,
m - число разновидностей результативного
признака; Аi - итоговые
частоты по строкам; Вj -
итоговые частоты по столбцам.
Коэффициенты меняются от 0 до 1, но коэффициент Чупрова яв-ляется более точным показателем, т.к. учитывает число групп по каждому признаку.
Тесты
Какой показатель применяется для оценки тесноты связи меж-ду факторами?
коэффициент вариации; 3) t – статистика;
коэффициент детерминации; 4) F – критерий.
2. Какой показатель тесноты связи изменяется в пределах от -1 до +1?
эмпирическое корреляционное отношение; 2) коэффициент детерминации; 3) парный коэффициент корреляции; 4) коэффициент эластичности.
3. Как рассчитывается парный коэффициент корреляции?
1)
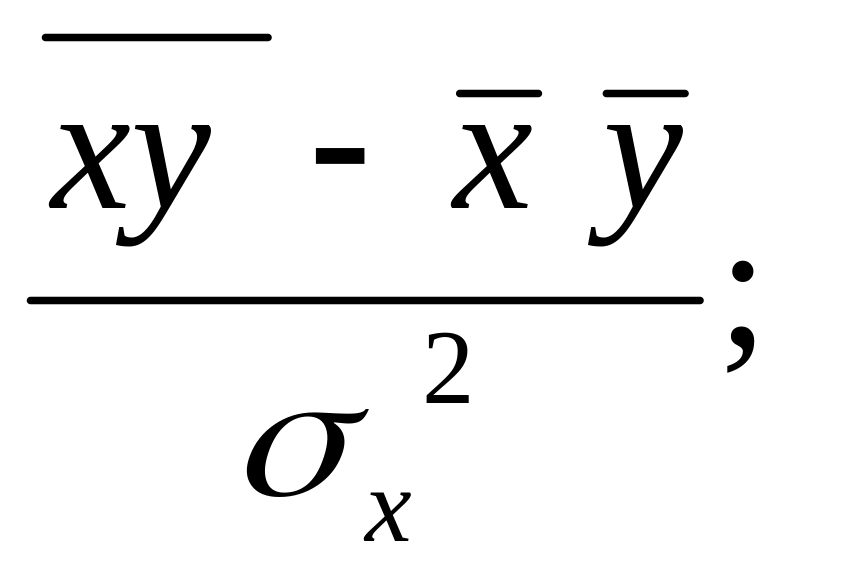 2)
2)
![]() 3)
3)
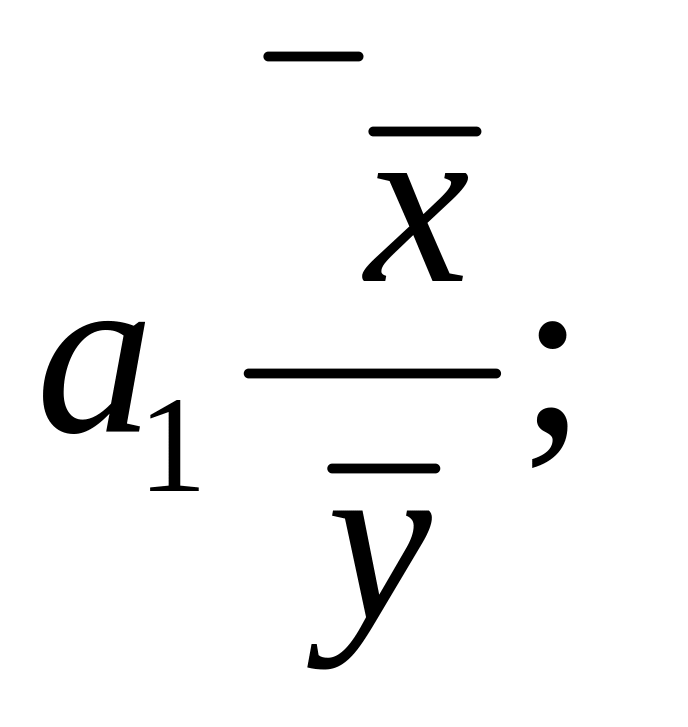 4)
4)
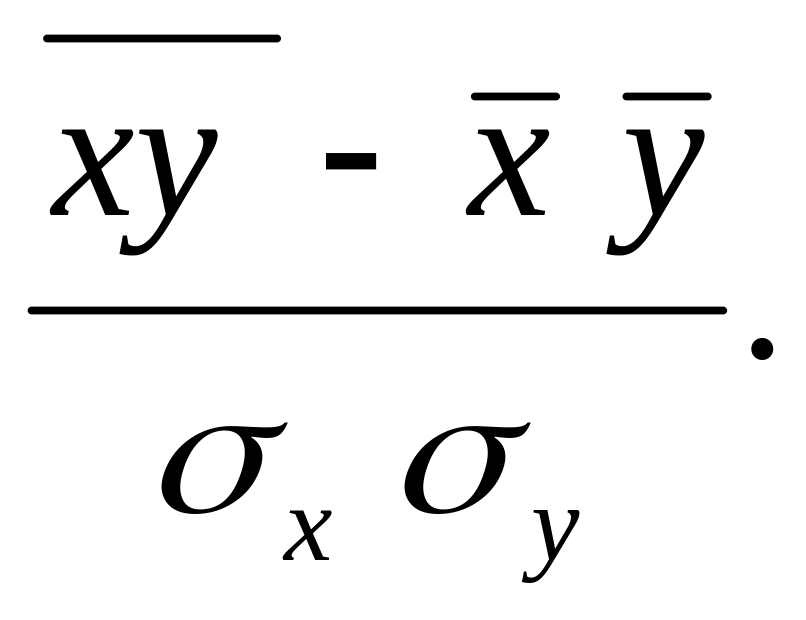
4. Какая задача решается при определении коэффициента детерминации?
оценка тесноты и направления связи; 2) оценка тесноты связи; 3) какая часть вариации у зависит от вариации х? 4) эластичность изменения у от изменения х.
5. На основе какого соотношения проверяется статистическая однородность распределения факторного признака?
1) коэффициента корреляции; 3) корреляционного отношения;
2) коэффициента вариации; 4) коэффициента эластичности.
6. Какие характеристики не относятся к параметрическим показателям тесноты связи:
1) коэффициент Фехнера; 3) коэффициент ранговой корреляции;
2) коэффициент конкордации; 4) корреляционное отношение.
7. Для взаимосвязи между альтернативными признаками применяется:
коэффициент взаимной сопряженности; 2) коэффициент контингенции; 3) коэффициент конкордации; 4) коэффициент корреляции
8.
Какой показатель рассчитывается по
формуле:
![]()
парный коэффициент корреляции; 2) коэффициент детерминации; 3) коэффициент эластичности; 4) частный коэффициент корреляции.
9. Какой показатель применяется для оценки уровня статистической точности уравнения связи?
1)
t
-критерий; 2) F
–критерий; 3)
![]() критерий;
4)
критерий;
4)
![]()
