
- •Министерство образования и науки украины донецкий национальный университет
- •По теории статистики
- •Скоробогатова Нелля Вікторівна
- •(Російською мовою)
- •Тема 1. Статистическое наблюдение Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 2. Сводка и группировка данных Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 3. Графический метод Методические указания
- •Беларусь
- •10. Что такое графический образ?
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 5. Анализ рядов распределения. СтаТиСтическая проверка гипотез Методические указания
- •Решение типовых задач
- •Решение
- •Распределение студентов по успеваемости
- •Решение
- •Решение
- •Кумулятивные показатели распределения семей по среднедушевому доходу
- •Вспомогательная таблица для расчета теоретических частот нормального распределения
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 6. Выборочное наблюдение Методические указания
- •Формулы необходимого объема выборки для различных способов формирования выборочной совокупности выводятся из соответствующих соотношений, используются при расчете предельных ошибок выборки.
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 7. Анализ интенсивности динамики Методические указания
- •Формулы показателей анализа ряда динамики
- •1. Что характеризует уровень ряда динамики?
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 8. Анализ тенденций развития Методические указания
- •Уравнения, используемые при аналитическом выравнивании динамических рядов
- •Решение типовых задач
- •Решение
- •Вспомогательные расчеты для определения параметров а0 и а1 уравнения прямой и критерия статистической точности аналитического уравнения
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Тема 9. Индексы Методические указания
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Тема 10. Статистические методы изучения
- •ВзаимОсвязей социально-экономических
- •Явлений
- •Методические указания
- •Шкала Чеддока
- •На основе данных аналитической группировки строится график эмпирической линии связи, вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о ее форме.
- •Системы нормальных уравнений для разных форм связи
- •3) Рассчитывается коэффициент ранговой корреляции Спирмена ( ): ;
- •Решение типовых задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Вспомогательная таблица для расчета параметров уравнения связи
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •Ответы на тестовые задания
- •Ответы к задачам
- •Тема 10
1. Что характеризует уровень ряда динамики?
отношение показателя за один период к другому; 2) величину явления на определенную дату или за определенный период; 3) на сколько единиц своего измерения данный показатель отличается от другого; 4) относительную оценку абсолютного прироста.
В каких единицах измеряется абсолютный прирост?
в коэффициентах; 3) в гривнах;
в единицах измерения уровня ряда; 4) в процентах.
3. По какой формуле исчисляется базисный абсолютный прирост?
1)
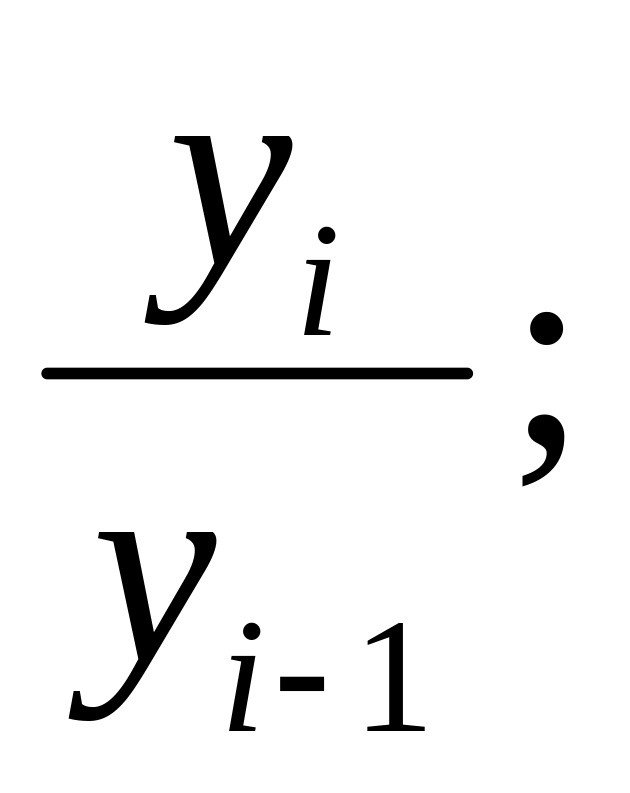 2)
2)
![]() 3)
3)
![]() 4)
4)
4. Какая формула используется для расчета цепного темпа роста?
1)
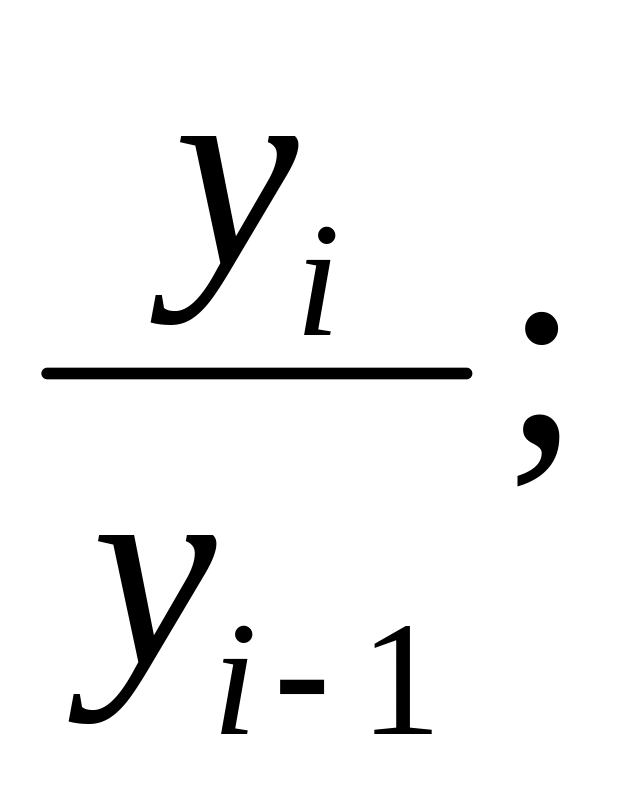 2)
3)
2)
3)
![]() 4)
4)![]()
5. По какой формуле можно определить базисные темпы прироста?
1)
2)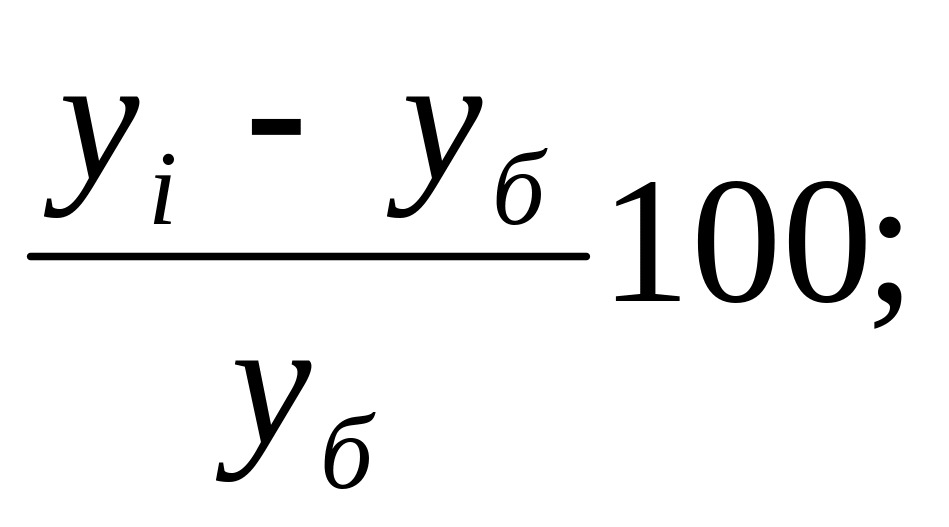 3)
4)
3)
4)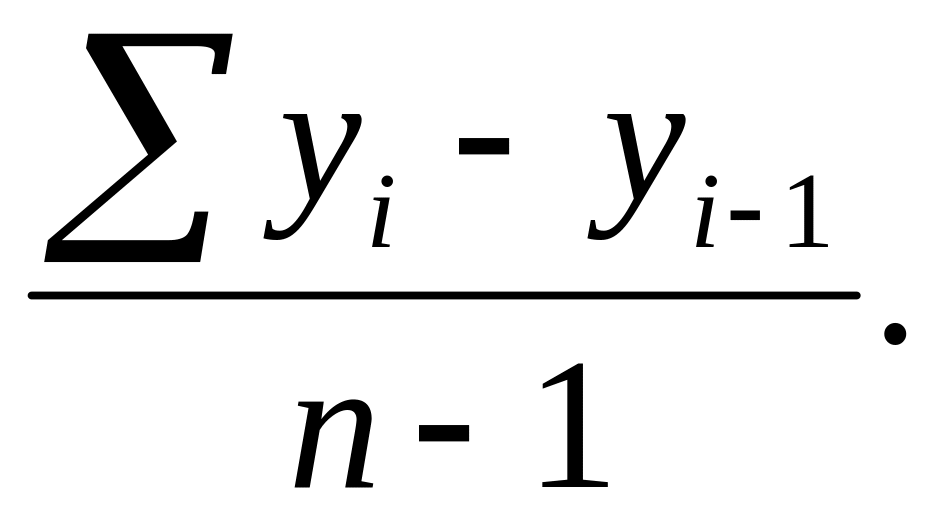
6. Какую формулу можно использовать для определения абсолютного значения 1% прироста?
1)
2)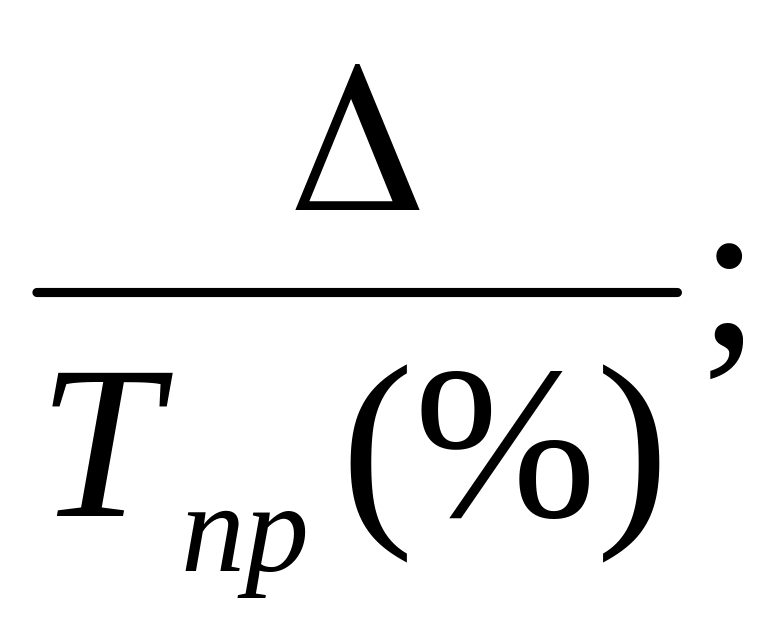 3)
3)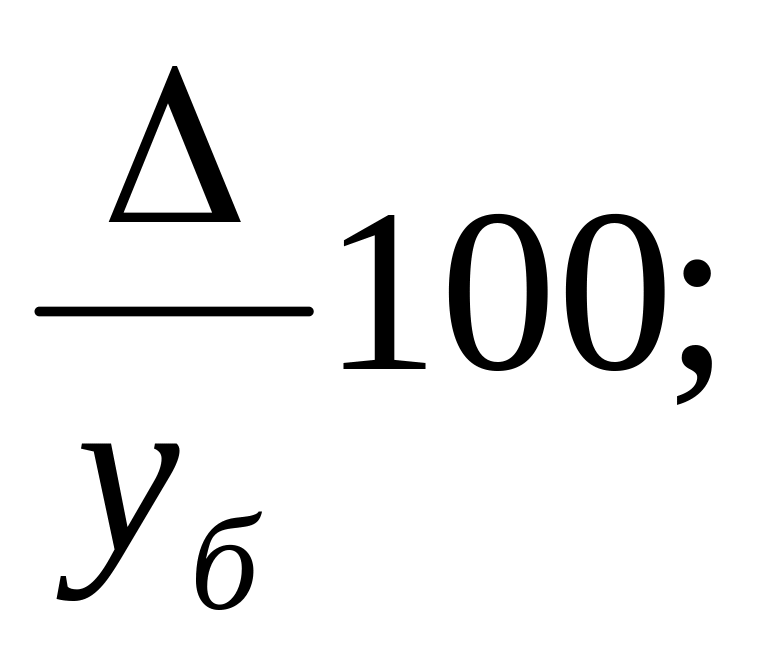 4)
4)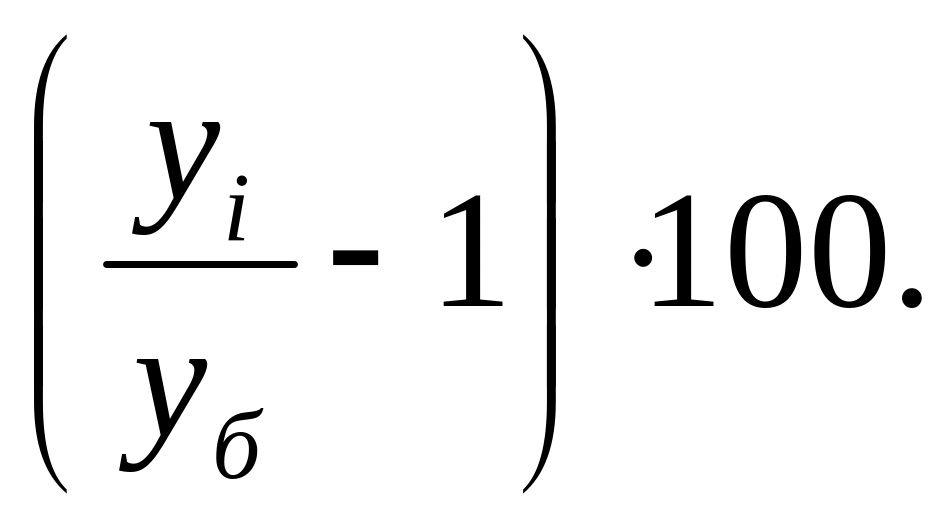
7. По какой формуле исчисляется средний абсолютный прирост?
1)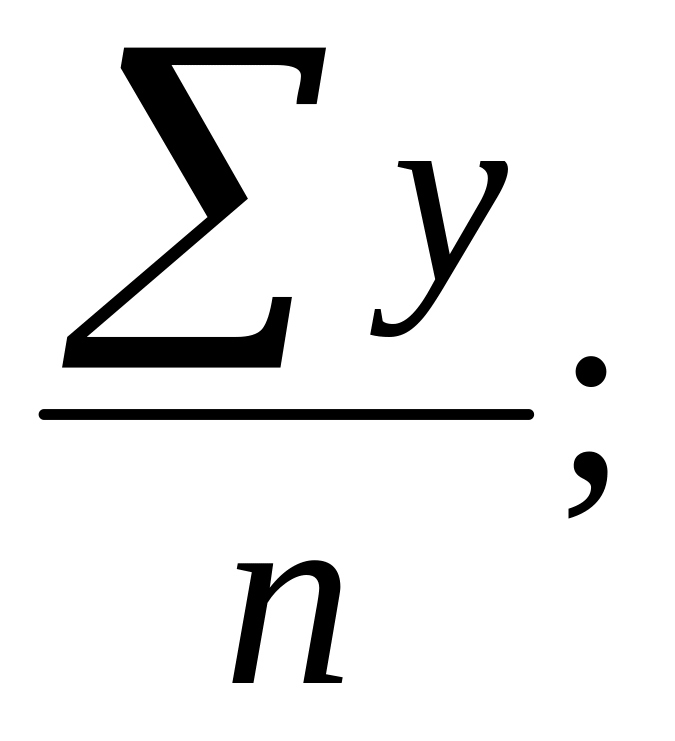 2)
2)
 3)
3)
 4)
4)
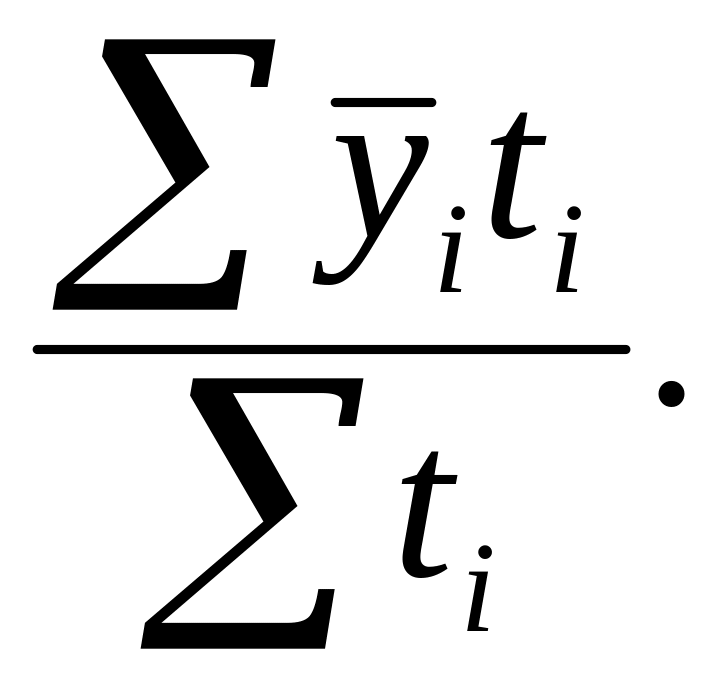
8. По какой формуле находится средний темп роста?
1)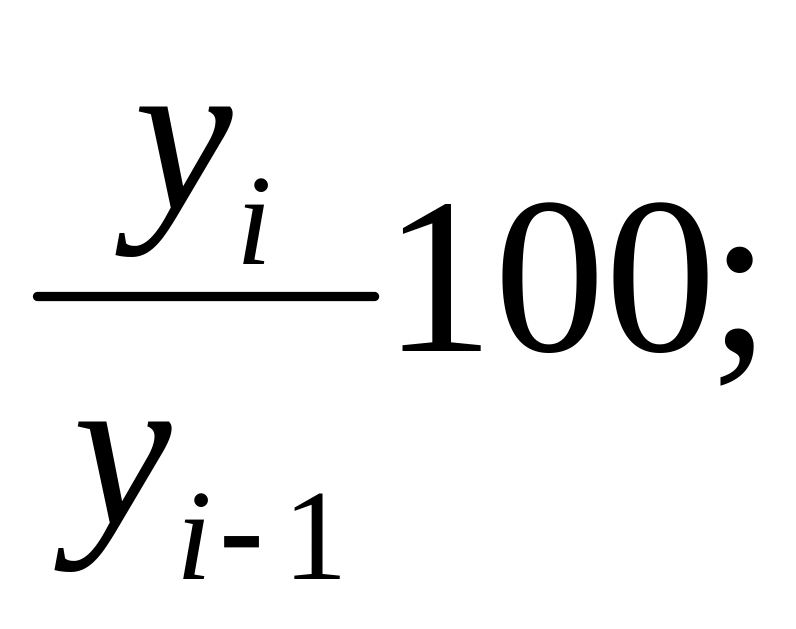 2)
2)
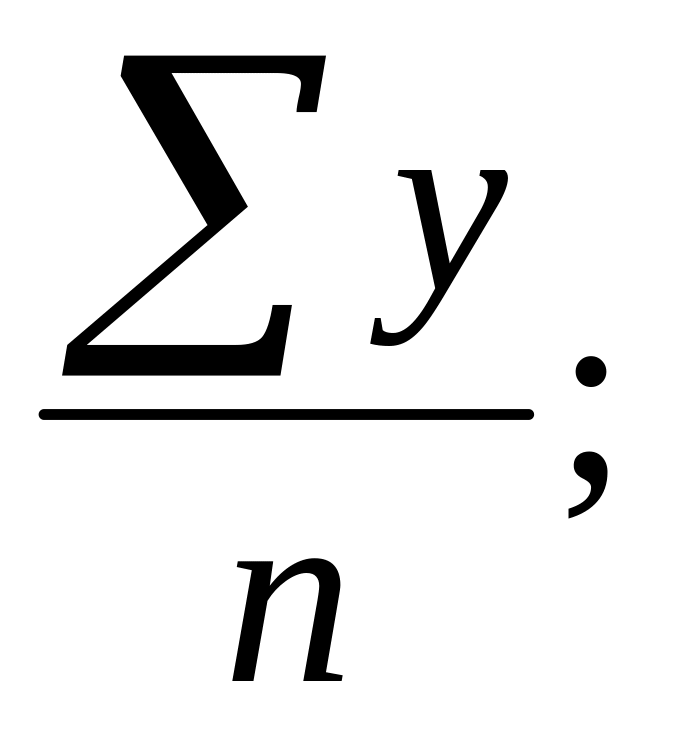 3)
3)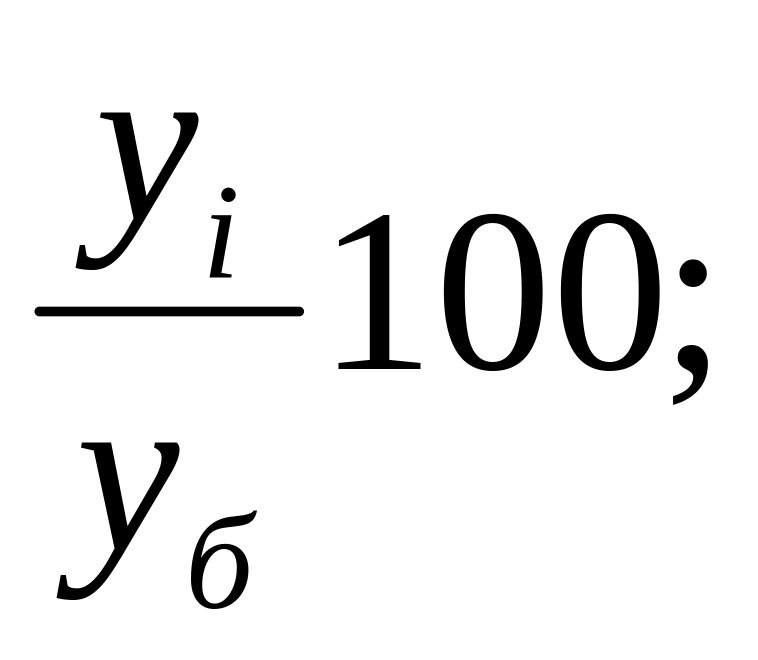 4)
4)
![]()
Какую формулу можно использовать для исчисления среднего уровня моментного ряда с равными интервалами времени между датами?
1)
2)
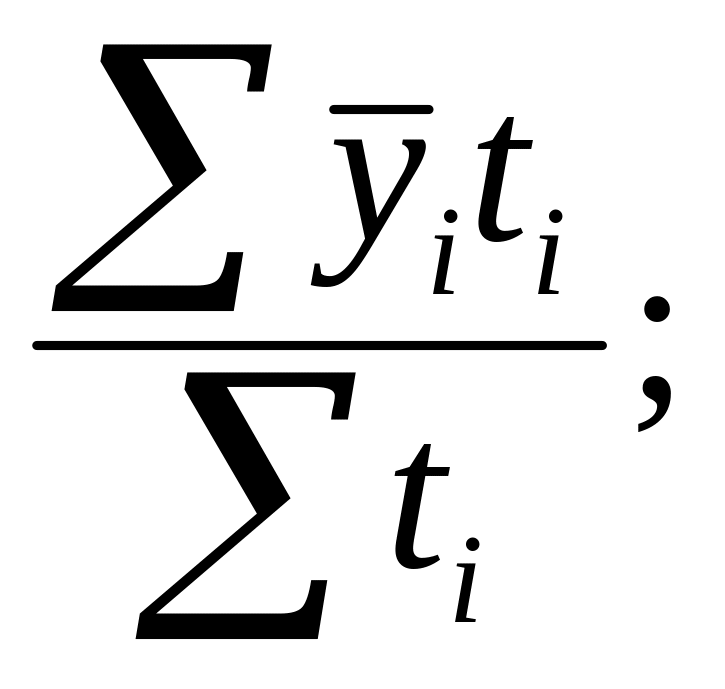 3)
3)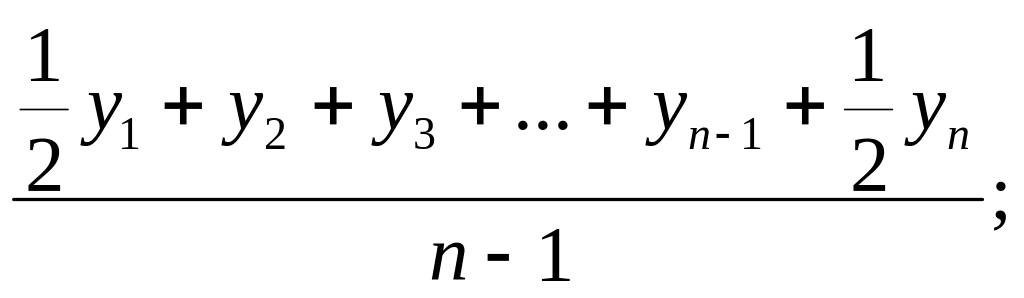 4)
4)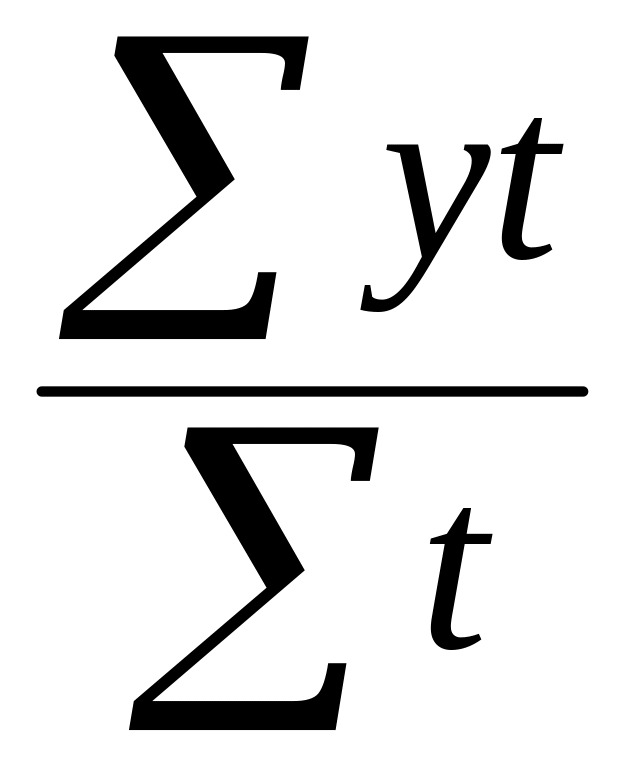 .
.
10. По какой формуле вычисляется средний уровень интервального ряда динамики с равными интервалами?
1)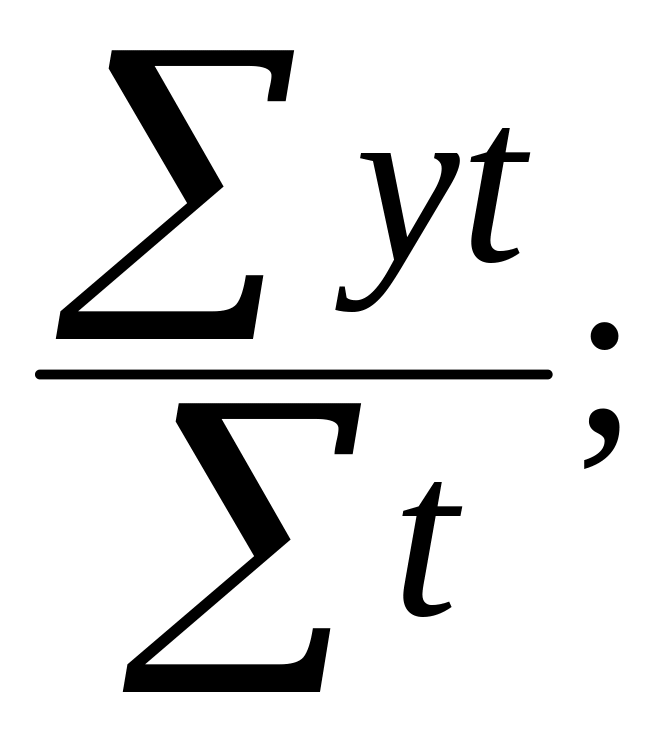 2)
3)
4)
2)
3)
4)
Решение типовых задач
Пример 1. Провести анализ динамики прямых иностранных инвестиций в регион за 1999 – 2002гг.
Годы 1999 2000 2001 2002
Иностранные инвестиции, млн.долл.США 5,0 4,6 5,3 6,4
Решение
1. Для выражения
абсолютной скорости роста (снижения)
уров-ня ряда динамики рассчитывается
абсолютный прирост![]() .
.
Базисный способ:
![]()
![]() =
4,6 - 5,0 = -0,4млн.долл;
=
4,6 - 5,0 = -0,4млн.долл;
![]() =
5,3 - 5,0 = 0,3млн.долл;
=
5,3 - 5,0 = 0,3млн.долл;
![]() =
6,4 - 5,0 = 1,4млн.долл.
=
6,4 - 5,0 = 1,4млн.долл.
Следовательно, по сравнению с 1999г. иностранные инвестиции в регион в 2000г. снизились на 0,4 млн.долл., в 2001г. и 2002г. возросли соответственно на 0,3 и 1,4 млн.долл.
Цепной
способ:![]()
![]() =
4,6 -5,0 = - 0,4млн.долл.;
=
4,6 -5,0 = - 0,4млн.долл.;
![]() = 5,3 - 4,6 = 0,7млн.долл.;
= 5,3 - 4,6 = 0,7млн.долл.;
![]() =
6,4 - 5,3 = 1,1млн.долл.
=
6,4 - 5,3 = 1,1млн.долл.
Следовательно, ежегодно по сравнению с предыдущим годом иностранные инвестиции изменялись так: в 2000г. снизились на 0,4млн.долл., в 2001г. возросли на 0,7млн.долл. и в 2002г. увеличи-лись на 1,1млн. долл.
2. Интенсивность изменения уровней ряда динамики оценивается с помощью темпа роста (Т).
Базисный способ: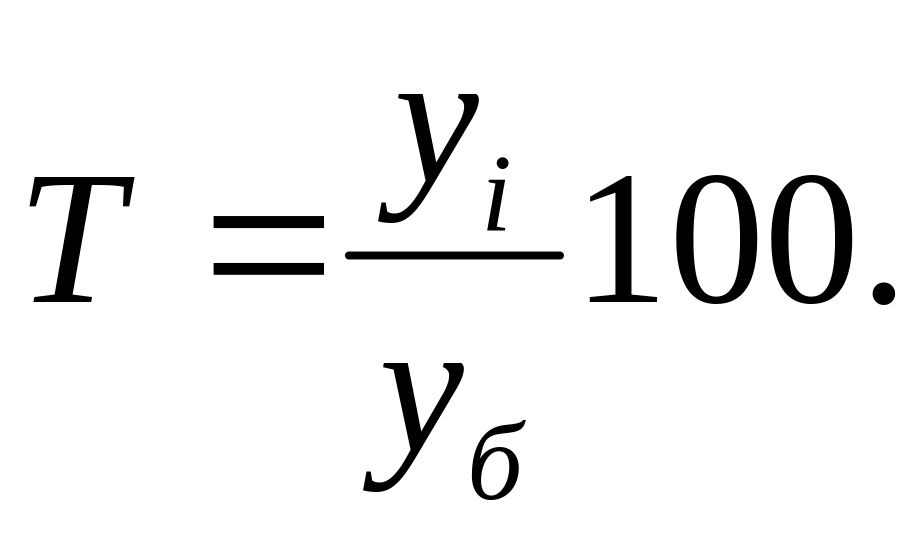
![]() =
=
 =
92,0%;
=
92,0%;
![]() =
=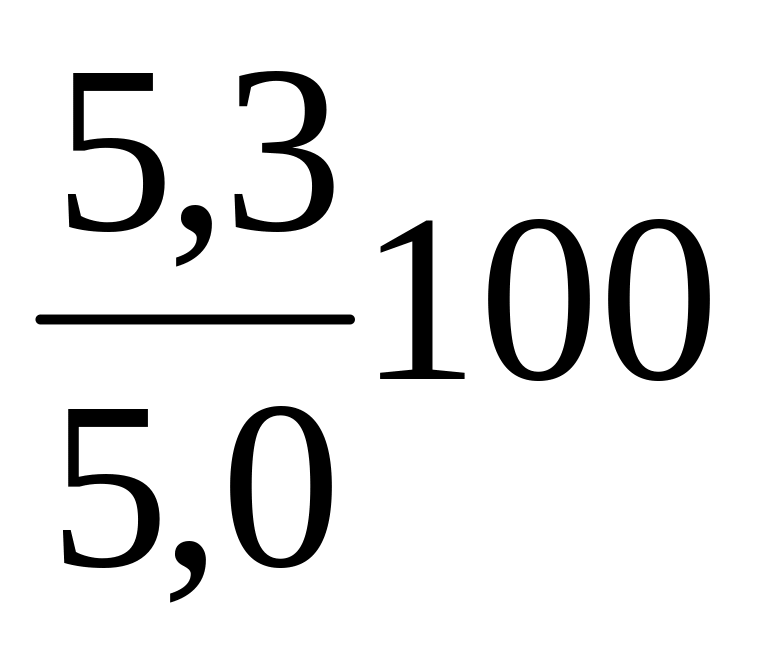 =
106,0%;
=
106,0%;
![]() =
=
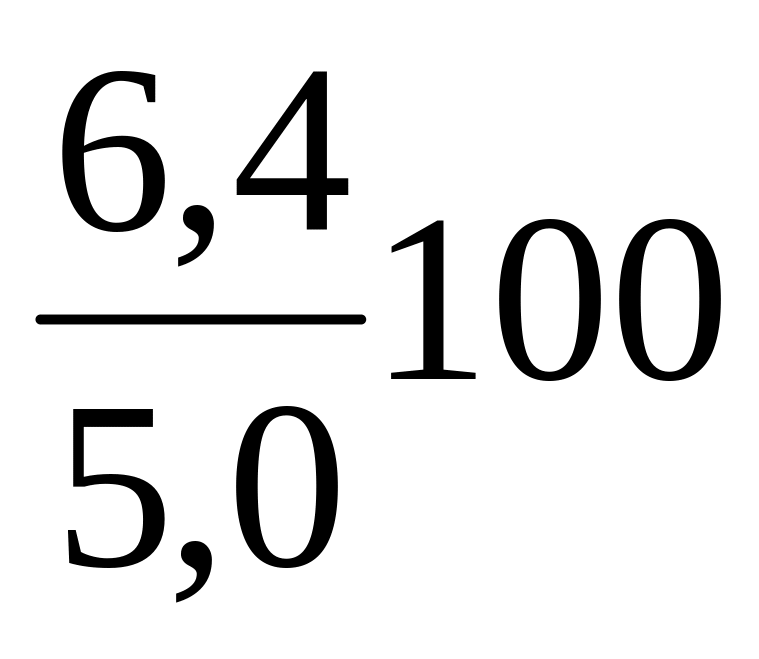 = 128,0% .
= 128,0% .
Таким образом, по сравнению с 1999г. иностранные инвестиции в 2000г. снизились в 0,92 раза, в 2001г. и в 2002г. увеличились соответственно в 1,06 и 1,28 раза.
Цепной способ:

![]() =
=
92,0%;
=
=
92,0%;
![]() =
=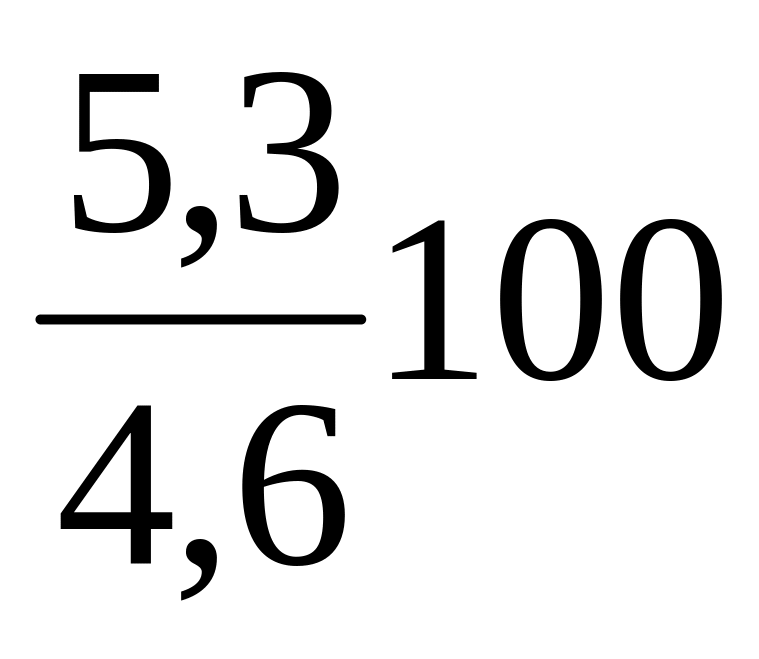 =
115,2%;
=
115,2%;
![]() =
=
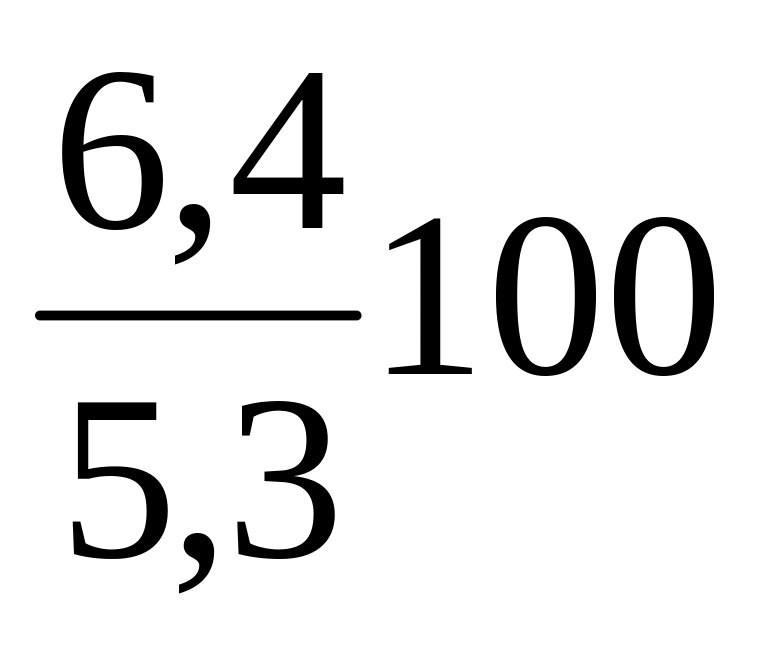 = 120,8%.
= 120,8%.
Следовательно, ежегодно по сравнению с предыдущим годом иностранные инвестиции изменялись так: в 2000г. их объем снизился в 0,92 раза, в 2001г. возрос в 1,152 раза, в 2002г. увеличился в 1,028 раза.
3. Для выражения
изменения величины абсолютного прироста
уровней ряда динамики в относительном
выражении определяется темп прироста
(![]() ).
В случае, когда уже исчислены темпы
роста, темпы прироста целесообразно
определять по следующим формулам.
).
В случае, когда уже исчислены темпы
роста, темпы прироста целесообразно
определять по следующим формулам.
Базисный
способ:
![]() или
или
![]()
![]() = 92 - 100 = - 8%;
= 92 - 100 = - 8%;
![]() =106 - 100 = 6%;
=106 - 100 = 6%;
![]() = 128 - 100 = 28%.
= 128 - 100 = 28%.
Это означает, что иностранные инвестиции в регион по сравнению с 1999г. в 2000г. снизились на 8 %, в 2001г. возросли на 6 %, а в 2002г. увеличились на 28 %.
Цепной способ:
![]() или
или
![]()
![]() =
92 -100 = - 8%;
=
92 -100 = - 8%;
![]() =1
15,2 -100 = 15,2%;
=1
15,2 -100 = 15,2%;
![]() =
120,8 -100 = 20,8%.
=
120,8 -100 = 20,8%.
Следовательно, ежегодно по сравнению с предыдущим годом иностранные инвестиции изменялись так: в 2000г. снизились на 8 %, в 2001г. возросли на 15,2 %, в 2001г. тоже увеличились на 20,8 %.
4. Определим
показатель абсолютного значения 1%
прироста. Его расчет на цепной основе
будет следующим: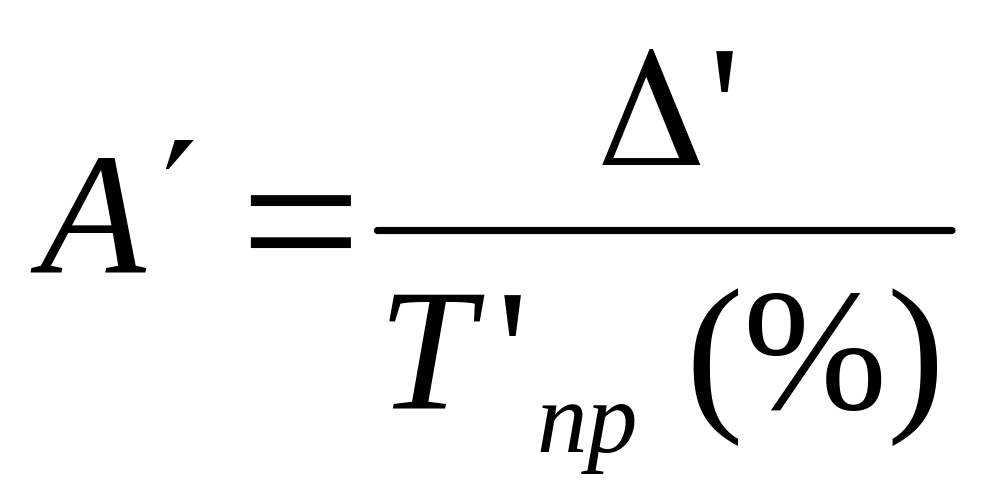
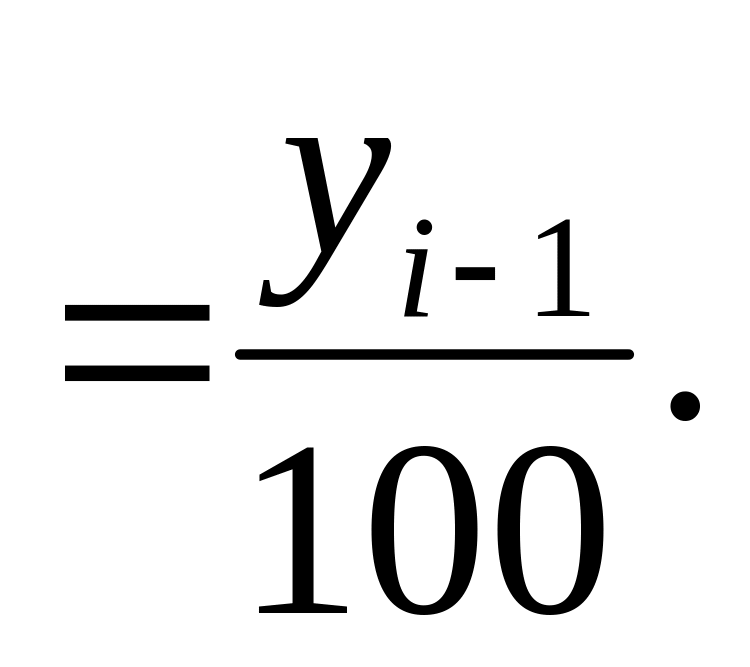
Для 2000г. этот показатель равен 5 : 100 = 0,050 млн.долл, для 2001г: 4,6 : 100 = 0,046млн.долл, для 2002г: 5,3 : 100 = 0,053млн.долл.
Таким образом, в 2000г. на каждый процент снижения инвестиций приходилось 0,05 млн.долл, в 2001г. на один процент прироста инвестиций приходилось 0,046 млн.долл., в 2002г. – 0,053 млн.долл. Итоги расчетов аналитических показателей изучаемого ряда динамики для наглядности рекомендуется представлять в таблице ( табл.7.2).
Таблица 7.2
Показатели анализа динамики иностранных
инвестиций в регион за 1999 – 2002 гг.
Годы |
Инстран-ные инвес-тиции,млн. долл США |
Абсолютный прирост,млн. долл США |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста(цеп ной способ), млн.долл.США |
|||
базисный способ |
цепной способ |
базисный способ |
цепной способ |
базисный способ |
цепной способ |
|||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1999 |
5,0 |
- |
- |
100,0 |
- |
- |
- |
- |
2000 |
4,6 |
-0,4 |
-0,4 |
92,0 |
92,0 |
-8,0 |
-8,0 |
0,050 |
2001 |
5,3 |
0,3 |
0,7 |
106,0 |
115,2 |
6,0 |
15,2 |
0,046 |
2002 |
6,4 |
1,4 |
1,1 |
128,0 |
120,8 |
28,0 |
20,8 |
0,053 |
Данный ряд динамики по своему виду является интерваль-ным, поэтому средний уровень определяется по формуле:
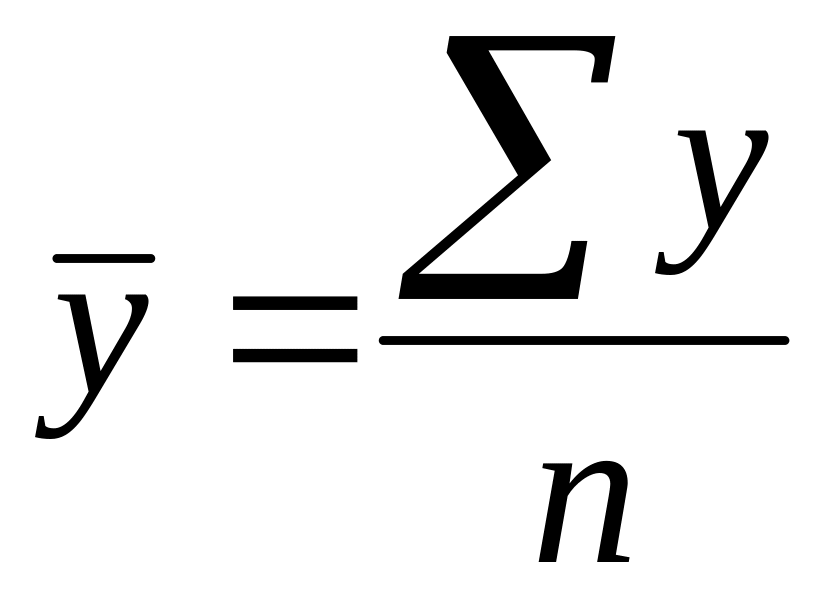 =
=
=
=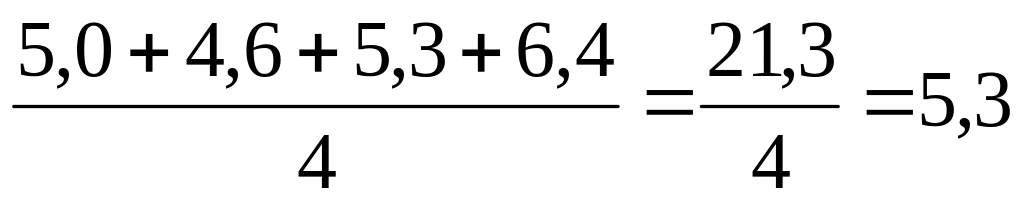 млн.долл.
млн.долл.
Это означает, что в среднем ежегодно иностранные инвестиции в регион составляли 5,3 млн.долл.
6. Средний абсолютный прирост определяется так:
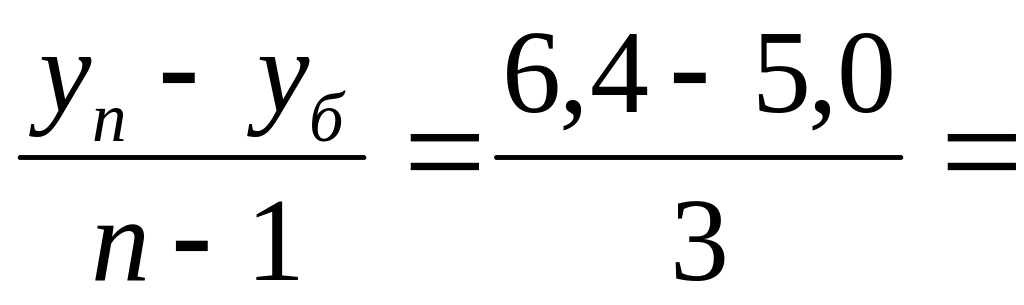 0,47
млн. долл. Это означает, что в среднем
ежегодно иностранные инвестиции
возрастали на 0,47 млн.долл.
0,47
млн. долл. Это означает, что в среднем
ежегодно иностранные инвестиции
возрастали на 0,47 млн.долл.
7. В нашем примере
средний темп роста составит: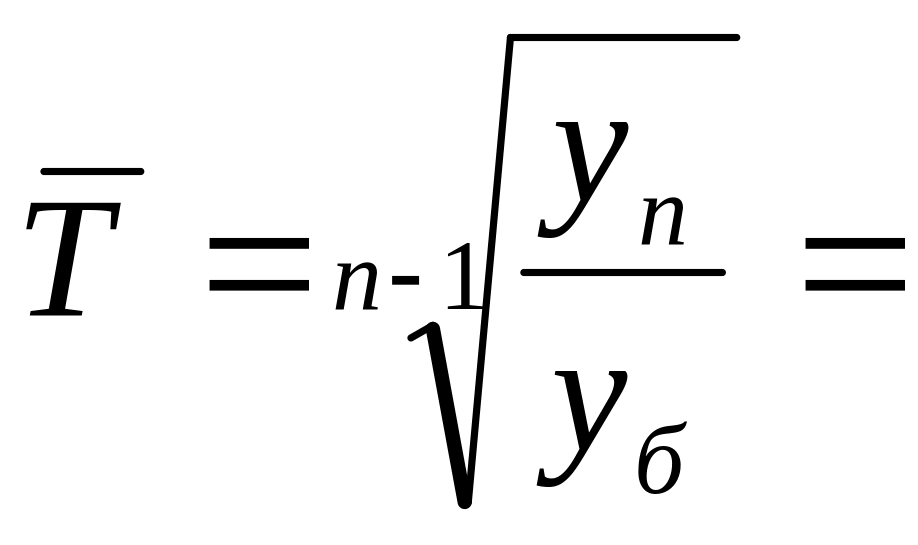
![]() или 108,5%, т.е. в
среднем ежегодно иностранные инвестиции
возрастали в 1,085 раза.
или 108,5%, т.е. в
среднем ежегодно иностранные инвестиции
возрастали в 1,085 раза.
8. По данным нашего
примера средний темп прироста будет
таким:![]() ,
т.е. в среднем ежегодно иностранные
инвестиции увеличивались на 8,5%.
,
т.е. в среднем ежегодно иностранные
инвестиции увеличивались на 8,5%.
9. Рассчитаем
среднее абсолютное значение одного
процента прироста:
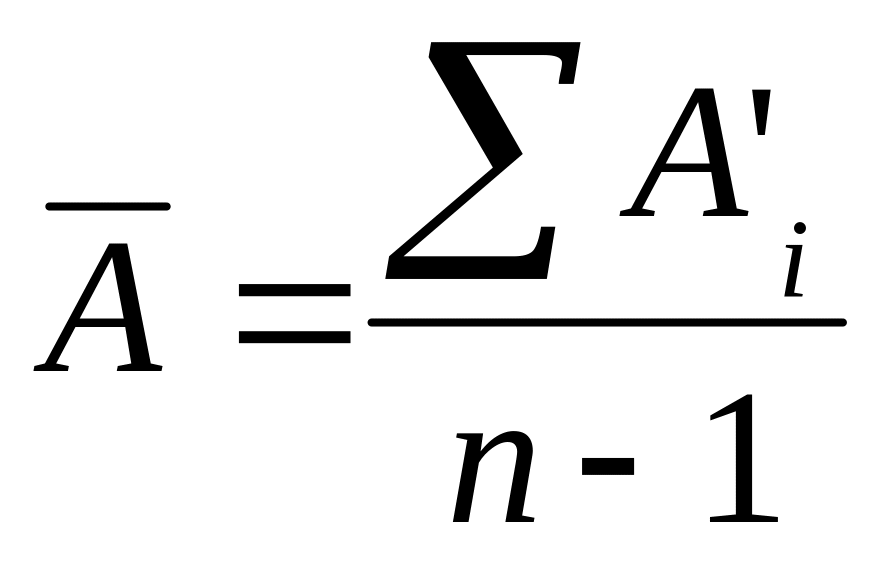
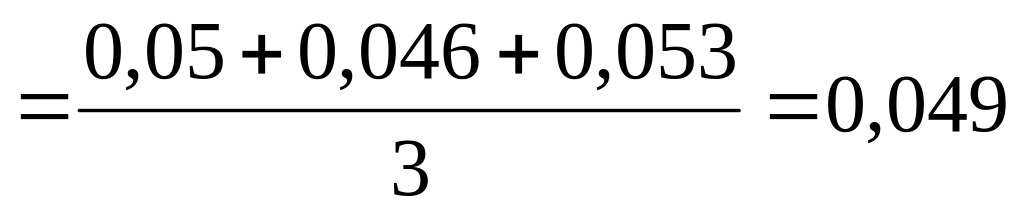 млн.грн. Следова-тельно, в среднем
ежегодно на каждый процент прироста
иностранных инвестиций приходилось
0,049 млн. грн.
млн.грн. Следова-тельно, в среднем
ежегодно на каждый процент прироста
иностранных инвестиций приходилось
0,049 млн. грн.
Пример 2. В I квартале отчетного года списочная численность работников предприятия составляла: на 01.01 – 32, на 01.02 - 36, на 01.03 – 27, на 01.04 - 34 человека. Определим среднюю списочную численность работников за квартал.
