Решение

1. Средняя годовая стоимость основных фондов в генеральной совокупности определяется по формуле: .

Предельная ошибка рассчитывается так: .

При собственно-случайном бесповторном отборе определяется по формуле: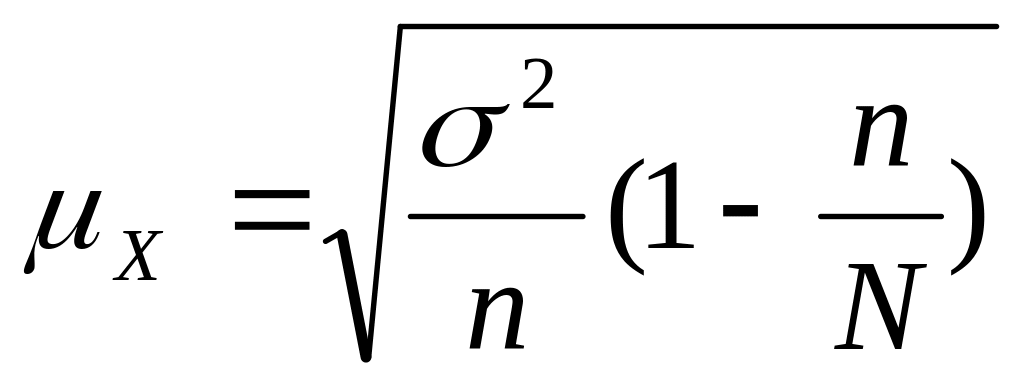 . Для расчета средней и дисперсии по выборочной совокупности построим таблицу 6.3.

Таблица 6.3

Вспомогательные расчеты для определения средней и

дисперсии по результатам выборки

Средняя годовая стоимость основных фондов, млн. грн	Кол-во заводов	Дискрет ный ряд,			( )2	( )2f
До 4	7	3	21	- 3,4	11,56	80,92
4 – 6	12	5	60	- 1,4	1,96	23,52
6 – 8	21	7	147	0,6	0,36	7,56
Свыше 8	10	9	90	2,6	6,76	67,60
Итого:	50	-	318	-	-	179,60

Средняя в вариационном ряду, т.е. по выборочной совокупнос-ти, рассчитывается следующим образом: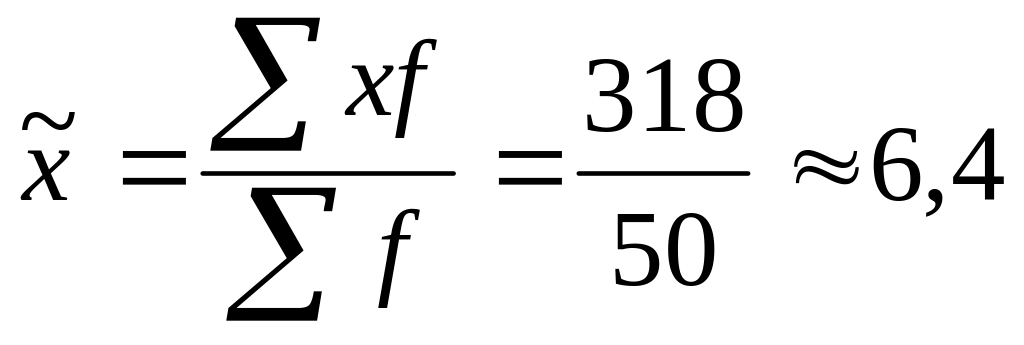 млн.грн.

Дисперсию определим по формуле: .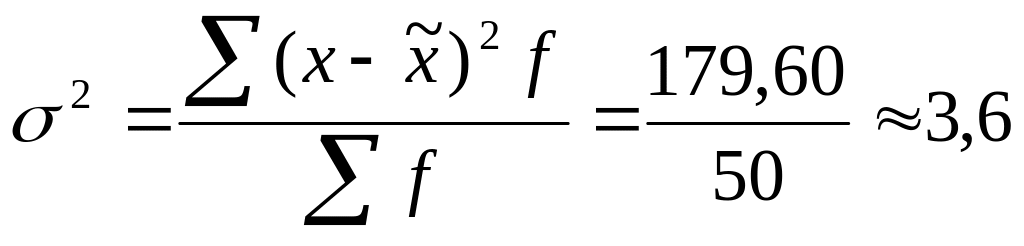

N = 500, т. к. по условию задачи объем выборки составляет 10% от генеральной совокупности (n = 50). Тогда средняя ошибка выборки составит: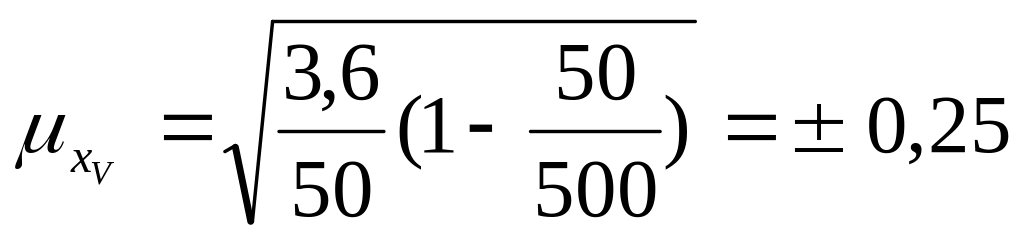 млн.грн.

В нашем примере задана вероятность 0,997, при которой , и предельная ошибка выборки будет равна: млн.грн.

Средняя годовая стоимость основных фондов в генеральной совокупности будет находиться в пределах:

= 6,4млн.грн. 0,75 млн.грн; 5,65 млн.грн 7,15млн.грн.

Следовательно, с вероятностью 0,997 можно утверждать, что средняя годовая стоимость основных фондов в генеральной совокупности будет находиться в пределах от 5,65 до 7,25 млн.грн.

2. Доля заводов со стоимостью основных фондов свыше 6 млн.грн в генеральной совокупности определяется по формуле: .

Доля таких заводов в выборочной совокупности будет следующей: ; .

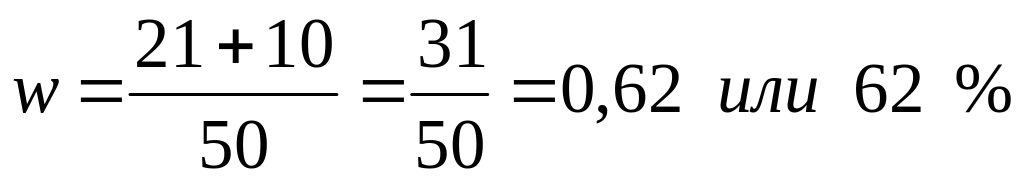В нашем примере задана вероятность 0,954, поэтому .

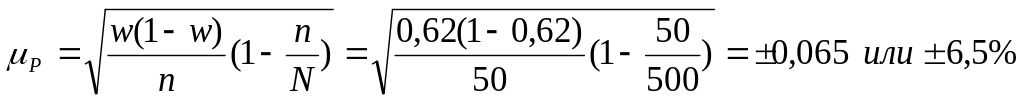
Тогда доля заводов, имеющих стоимость основных фондов свыше 6 млн.грн., в генеральной совокупности составит:

; .

Таким образом, доля заводов со стоимостью основных фондов свыше 6 млн.грн во всей генеральной совокупности будет находиться в пределах от 49 до 75%. Результат гарантируется с вероятностью 0,954.

Пример 2. Для определения средней месячной заработной платы работников финансово-банковских учреждений было проведено выборочное обследование 100 сотрудников по схеме собственно-слу-чайного повторного отбора. В результате установлено, что средняя зарплата составляет 880 грн. при среднем квадратическом отклонении 169 грн. С вероятностью 0,954 определите пределы, в которых находится средняя зарплата в генеральной совокупности.

Решение

Средняя зарплата работников в генеральной совокупности будет определяться по формуле: . Для определения границ генеральной средней необходимо вычислить предельную ошибку выборки: ; ; 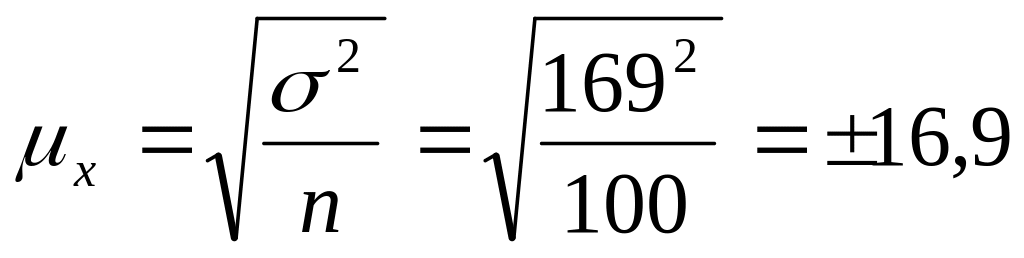грн.; грн; 880 ± 33,8; 846,2 грн. 913,8 грн.

С вероятностью 0,954 можно утверждать, что средняя зарплата работников финансово-банковских учреждений в генеральной совокупности находится в пределах от 846,2 до 913,8 грн.

Пример 3. В процессе осуществления технического контроля из партии готовой продукции методом случайного бесповторного отбора было проверено 80 изделий, из которых 4 оказались бракованными. С вероятностью 0,954 определите пределы бракованной продукции во всей, если процент отбора равен 10.