
- •§ 2. Свойства определителей 2-го и 3-го порядка.
- •§ 3. Миноры и алгебраические дополнения элементов матрицы 3-го порядка.
- •§ 4. Разложение определителя 3-го порядка по строке или столбцу.
- •§ 5. Определители 4-го порядка.
- •§ 6. Определители n-го порядка.
- •§ 1. Виды матриц, равенство матриц.
- •§ 2. Линейные действия с матрицами и их свойства.
- •§ 3. Умножение матриц и его свойства.
- •§ 4. Обратная матрица и ее свойства.
- •§ 5. Ранг матрицы.
- •§ 1. Основные понятия.
- •§ 2. Решение систем линейных уравнений по формулам Крамера.
- •§ 3. Решение систем линейных уравнений матричным способом.
- •§ 4. Исследование систем линейных уравнений.
- •§ 5. Решение систем линейных уравнений методом Гаусса.
- •§ 6. Однородные системы линейных уравнений.
- •Тема 1. О п р е д е л и т е л и
- •Тема 2. М а т р и ц ы
- •Тема 3. С и с т е м ы л и н е й н ы х у р а в н е н и й
- •§ 2. Линейные действия с векторами и их свойства.
- •§ 3. Линейные векторные пространства. Понятие базиса.
- •§ 4. Разложение вектора по базису.
- •§ 1. Проекция вектора на ось и ее свойства.
- •§ 2. Скалярное произведение векторов и его свойства.
- •§ 3. Векторное произведение векторов и его свойства.
- •§ 4. Смешанное произведение векторов и его свойства.
- •§ 1. Основные понятия.
- •§ 2. Линейные действия с векторами в ортонормированном базисе.
- •§ 3. Произведения векторов в координатах относительно ортонормированного базиса.
- •§ 4. Вычисление модуля, направляющих cos - ов и проекций векторов.
- •§ 1. Деление отрезка в данном отношении.
- •§ 2. Вычисление расстояния между двумя точками и угла между двумя векторами.
- •§ 3. Вычисление площадей и объемов.
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
§ 6. Однородные системы линейных уравнений.
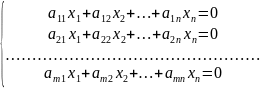
Однородная система
всегда совместна, т.к. имеет нулевое
решение: X =
 .
.
Если rang A = n, то система имеет только нулевое решение.
Если rang A < n, то система имеет еще и ненулевые решения.
В случае, когда число уравнений системы равно числу неизвестных (m = n), эти условия означают следующее:
если det A ≠ 0, то система имеет только нулевое решение;
если det A = 0, то система имеет еще и ненулевые решения.
Общее решение однородной системы линейных уравнений имеет вид:
X = c1 X1 + c2 X2 + … + c n - r X n - r ,
где X1, X2, … , X n - r - фундаментальная система решений (ФСР), c i произвольные числа, r = rang A.
Пример. Найти общее решение однородной системы линейных уравнений и сделать проверку.
Указать ФСР (фундаментальную систему решений).
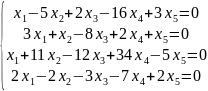
Применим метод Гаусса. n = 5 - число неизвестных.
A =
 [из 2-й строки
вычтем 1-ю строку, умноженную на 3; из 3-й
[из 2-й строки
вычтем 1-ю строку, умноженную на 3; из 3-й
строки вычтем 1-ю строку; из 4-й строки вычтем 1-ю строку, умноженную на 2]
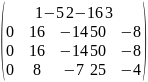 [из 2-й и 3-й строки вычтем 4-ю строку,
умноженную на 2]
[из 2-й и 3-й строки вычтем 4-ю строку,
умноженную на 2]
 [переставим 2-ю и 4-ю строку]
[переставим 2-ю и 4-ю строку]

r = rang A = 2, n - r = 3.


, - базисные переменные,
- базисные переменные,
 ,
,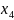 ,
, - свободные переменные.
- свободные переменные.
= c1, = c2, = c3, где c1, c2, c3 - произвольные числа.
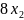 = 7c1 - 25c2
+ 4c3
=
= 7c1 - 25c2
+ 4c3
=
 (7c1
- 25c2 + 4c3).
(7c1
- 25c2 + 4c3).
Введем новые обозначения: С1 = c1, С2 = c2, С3= c3. Тогда получим:
= 8С 1, =8С 2, = 8С 3, = 7С 1 - 25С2 + 4С3,
= 5(7С 1 - 25С2 + 4С3) - 28С 1 + 168С 2 - 38С 3 = 19С 1 + 3С2 - 4С3.
Общее решение:
 ,
С1, С2, С3
R.
,
С1, С2, С3
R.
Проверка.
1-е уравнение:
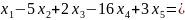
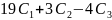
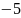 (
( )
)


 =
-
=
-



 =
- верное равенство.
=
- верное равенство.
Аналогично проверяются остальные 3 равенства.
Общее решение:
X =
 =
=
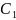
 +
+

 +
+

 ;
;
ФСР:
 .
.
Задачи по теме 3.
. Решить системы линейных уравнений по формулам Крамера.
1.
 2.
2.
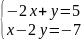
3.
 4.
4.
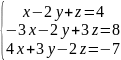
5.
 6.
6.

. Решить системы линейных уравнений матричным способом.
1.
 2.
2.
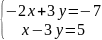
3.
 4.
4.

5.
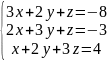 6.
6.

. Решить системы линейных уравнений методом Гаусса:
− исследовать систему по теореме Кронекера-Капелли;
− если система совместна, то найти общее решение в матричном виде и сделать проверку;
− если система совместна и неопределенна, то указать 3 частных решения в матричном виде.
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
 8.
8.

. Для однородной системы линейных уравнений найти общее решение в матричном виде и
сделать проверку. Указать фундаментальную систему решений.
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

Дополнительные задачи.
1. Найти многочлен P (x) 2-й степени, удовлетворяющий условиям: P (1) = -1, P (-1) = 9, P (2) = -3.
2. Найти многочлен P (x) степени не выше 2-х, удовлетворяющий условиям:
 , где
,
,
,
, где
,
,
,
 ,
,
 ,
,
 - заданные числа (
,
,
- различные числа).
- заданные числа (
,
,
- различные числа).
Следующие системы линейных уравнений исследовать на совместность и определенность в зависимости от значений λ, указать число базисных переменных r и число свободных переменных n - r:
3.
 4.
4.

5.
 6.
6.

Определить значения a, при которых однородная система линейных уравнений имеет ненулевые решения:
7.
 8.
8.
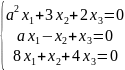
Найти фундаментальную систему решений (ФСР) следующих однородных систем линейных уравнений:
9.
 10.
10.
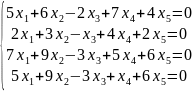
Найти общее решение следующих систем линейных уравнений:
11.
 12.
12.

О Т В Е Т Ы К З А Д А Ч А М
