
- •§ 2. Свойства определителей 2-го и 3-го порядка.
- •§ 3. Миноры и алгебраические дополнения элементов матрицы 3-го порядка.
- •§ 4. Разложение определителя 3-го порядка по строке или столбцу.
- •§ 5. Определители 4-го порядка.
- •§ 6. Определители n-го порядка.
- •§ 1. Виды матриц, равенство матриц.
- •§ 2. Линейные действия с матрицами и их свойства.
- •§ 3. Умножение матриц и его свойства.
- •§ 4. Обратная матрица и ее свойства.
- •§ 5. Ранг матрицы.
- •§ 1. Основные понятия.
- •§ 2. Решение систем линейных уравнений по формулам Крамера.
- •§ 3. Решение систем линейных уравнений матричным способом.
- •§ 4. Исследование систем линейных уравнений.
- •§ 5. Решение систем линейных уравнений методом Гаусса.
- •§ 6. Однородные системы линейных уравнений.
- •Тема 1. О п р е д е л и т е л и
- •Тема 2. М а т р и ц ы
- •Тема 3. С и с т е м ы л и н е й н ы х у р а в н е н и й
- •§ 2. Линейные действия с векторами и их свойства.
- •§ 3. Линейные векторные пространства. Понятие базиса.
- •§ 4. Разложение вектора по базису.
- •§ 1. Проекция вектора на ось и ее свойства.
- •§ 2. Скалярное произведение векторов и его свойства.
- •§ 3. Векторное произведение векторов и его свойства.
- •§ 4. Смешанное произведение векторов и его свойства.
- •§ 1. Основные понятия.
- •§ 2. Линейные действия с векторами в ортонормированном базисе.
- •§ 3. Произведения векторов в координатах относительно ортонормированного базиса.
- •§ 4. Вычисление модуля, направляющих cos - ов и проекций векторов.
- •§ 1. Деление отрезка в данном отношении.
- •§ 2. Вычисление расстояния между двумя точками и угла между двумя векторами.
- •§ 3. Вычисление площадей и объемов.
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
§ 4. Исследование систем линейных уравнений.
( )
A = - основная матрица системы ( ),
(A|B)=
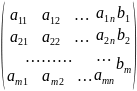 - расширенная матрица системы (
).
- расширенная матрица системы (
).
Теорема Кронекера-Капелли.
Для того чтобы система ( ) была совместной (т.е. имела решение), необходимо и достаточно, чтобы ранг основной матрицы был равен рангу расширенной матрицы системы:
( ) - совместна rang A = rang (A|B).
Пусть r = rang A = rang (A|B). Тогда:
1) при r = n система является определенной (т.е. имеет единственное решение);
2) при r < n система является неопределенной (т.е. имеет бесконечно много решений).
Пример. Исследовать систему:

(A|B)=
 [из 1-й строки
вычтем 3-ю строку, умноженную на 3; из
2-й
[из 1-й строки
вычтем 3-ю строку, умноженную на 3; из
2-й
строки вычтем 3-ю
строку, умноженную на 2]
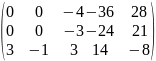
[1-ю строку разделим
на (-4); 2-ю строку разделим на (-3)]

[из 1-й строки вычтем
2-ю строку]
 [переставим 1-ю и
3-ю строки]
[переставим 1-ю и
3-ю строки]
 [переставим столбцы]
[переставим столбцы]
 .
.
Основная и расширенная матрица приведены к ступенчатым матрицам с 3-мя ненулевыми
строками. Следова тельно: rang A = rang (A|B) = r = 3.
По теореме Кронекера-Капелли система совместная. Так как r < n = 4, то система неопределенная.
Ответ: система является совместной и неопределенной (т.е. имеет бесконечно много решений).
§ 5. Решение систем линейных уравнений методом Гаусса.
( )
Метод Гаусса состоит из 2-х этапов.
1-й этап (прямой ход метода Гаусса):
Элементарными преобразованиями над расширенной матрицей система ( ) приводится к равносильной ей системе со ступенчатой расширенной матрицей.
2-й этап (обратный ход метода Гаусса):
Решается полученная равносильная система путем последовательного вычисления неизвестных, начиная с последнего уравнения.
Пример. Найти общее решение и сделать проверку; если система совместная и неопределенная, то указать 3 частных решения:
В предыдущем примере эта система была исследована: она является совместной и неопределенной: r = 3, n = 4. Расширенная матрица равносильной системы имеет вид:
Прямой ход метода Гаусса привел к равносильной системе:

Обратный ход метода Гаусса.
В качестве базисного
минора выберем минор
 .
.
Тогда базисными
переменными будут:
 , а свободной переменной:
, а свободной переменной:
 .
.

Свободная переменная
может принимать любое действительное
значение:
= c, c
R. Из
системы уравнений последовательно
находим все неизвестные:
 ,
,
 ,
,
 +3c.
+3c.
Общее решение:
 ,
c R.
,
c R.
Проверка. Подставим найденные значения неизвестных в исходную систему.
1-е уравнение:
 =
=
 =
=
 + 39 -
- 35 = 4 - верно;
+ 39 -
- 35 = 4 - верно;
2-е уравнение:
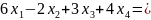

 + 26 -
- 21 = 5 - верно;
+ 26 -
- 21 = 5 - верно;
3-е уравнение:


 + 13 -
- 21 = -8 - верно.
+ 13 -
- 21 = -8 - верно.
Запишем общее решение в матричном виде.
X =
 =
=
 =
=
 +
+
 =
=

 +
,
c
R.
+
,
c
R.
Найдем частные решения системы (подставляя вместо «c» произвольные значения).
c =
0 X
=
;
c = 1
X =
 ;
c = 5
X =
;
c = 5
X =
 ;
;
Ответ. Общее решение: X = + , c R.
Частные решения: X1 = ; X2 = ; X3 = .
