
- •§ 2. Свойства определителей 2-го и 3-го порядка.
- •§ 3. Миноры и алгебраические дополнения элементов матрицы 3-го порядка.
- •§ 4. Разложение определителя 3-го порядка по строке или столбцу.
- •§ 5. Определители 4-го порядка.
- •§ 6. Определители n-го порядка.
- •§ 1. Виды матриц, равенство матриц.
- •§ 2. Линейные действия с матрицами и их свойства.
- •§ 3. Умножение матриц и его свойства.
- •§ 4. Обратная матрица и ее свойства.
- •§ 5. Ранг матрицы.
- •§ 1. Основные понятия.
- •§ 2. Решение систем линейных уравнений по формулам Крамера.
- •§ 3. Решение систем линейных уравнений матричным способом.
- •§ 4. Исследование систем линейных уравнений.
- •§ 5. Решение систем линейных уравнений методом Гаусса.
- •§ 6. Однородные системы линейных уравнений.
- •Тема 1. О п р е д е л и т е л и
- •Тема 2. М а т р и ц ы
- •Тема 3. С и с т е м ы л и н е й н ы х у р а в н е н и й
- •§ 2. Линейные действия с векторами и их свойства.
- •§ 3. Линейные векторные пространства. Понятие базиса.
- •§ 4. Разложение вектора по базису.
- •§ 1. Проекция вектора на ось и ее свойства.
- •§ 2. Скалярное произведение векторов и его свойства.
- •§ 3. Векторное произведение векторов и его свойства.
- •§ 4. Смешанное произведение векторов и его свойства.
- •§ 1. Основные понятия.
- •§ 2. Линейные действия с векторами в ортонормированном базисе.
- •§ 3. Произведения векторов в координатах относительно ортонормированного базиса.
- •§ 4. Вычисление модуля, направляющих cos - ов и проекций векторов.
- •§ 1. Деление отрезка в данном отношении.
- •§ 2. Вычисление расстояния между двумя точками и угла между двумя векторами.
- •§ 3. Вычисление площадей и объемов.
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Тема 4. Геометрические задачи
§ 2. Линейные действия с векторами в ортонормированном базисе.
1. Пусть даны координаты векторов и относительно О.Н.Б. { }:
 ,
,
 .
.
Тогда:
- при умножении вектора на число все его координаты умножаются на это число;
- при сложении (вычитании) векторов их координаты складываются (вычитаются):
λ
 ;
λ
;
λ
 ;
;
+
 ;
;
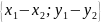 .
.
Условие коллинеарности векторов в координатной форме.
Векторы и коллинеарны тогда и только тогда, когда их
координаты пропорциональны:

Следствие.

2. Пусть даны координаты векторов и относительно О.Н.Б. { }:
 ,
,
 .
.
Тогда:
- при умножении вектора на число все его координаты умножаются на это число;
- при сложении (вычитании) векторов их координаты складываются (вычитаются):
λ
 ;
λ
;
λ
 ;
;
+
 ;
;
 .
.
Условие коллинеарности векторов в координатной форме.
Векторы
и
 коллинеарны тогда и только тогда,
когда их
коллинеарны тогда и только тогда,
когда их
координаты пропорциональны:
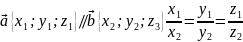
Следствие.


§ 3. Произведения векторов в координатах относительно ортонормированного базиса.
Пусть даны координаты векторов и относительно О.Н.Б. { }:
, .
Тогда:
 - скалярное произведение;
- скалярное произведение;
 - векторное произведение.
- векторное произведение.
Пусть даны координаты векторов , и относительно О.Н.Б. { }:
,
,
 .
Тогда:
.
Тогда:
 - смешанное произведение.
- смешанное произведение.
Если
векторы
,
и
лежат на плоскости, то
,
,
 и
и
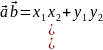 - скалярное произведение,
- скалярное произведение,
 -
векторное произведение,
-
векторное произведение,
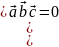 - смешанное произведение.
- смешанное произведение.
Пример.
,
 ,
,
 .
.
 = -7;
= -7;
 =
=

 +
+
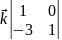 = 2
+ 4
+
;
= 2
+ 4
+
;
 =
1
=
1 0
2
0
2 = 4
0
2 = 2.
= 4
0
2 = 2.
Условия ортогональности, коллинеарности и компланарности векторов.
Пусть даны координаты векторов , и относительно О.Н.Б. { }:
, , .
Тогда:
 = 0
= 0
 =
=
,
,
- компланарны
 = 0
= 0
Пример.
Определить, при каких значениях λ векторы и будут ортогональны, если
= 2 - , = 3 + 2 , а векторы и заданы своими координатами относительно
О.Н.Б. {
}:
 ,
,
 .
.
= 0 (2 - )(3 + 2 ) = 0 6 - 3 + 4 - 2 = 0
4 + 4 - 3 = 0;
= 11 +

+ 00 = 1 +
2;
=
+ 11 + (-1)(-1)
=
2
+ 2;
=
+
+ 0 = 2
;
+ 00 = 1 +
2;
=
+ 11 + (-1)(-1)
=
2
+ 2;
=
+
+ 0 = 2
;
4(1 +
2)
+ 8
- 3(
2
+ 2) = 0
2
+ 8
- 2 = 0
1,2
= - 4
 3
.
3
.
Пример.
Определить,
при каких значениях λ векторы
,
и
 будут компланарны, если
будут компланарны, если
они заданы своими координатами относительно О.Н.Б. { }:
 ,
,
 ,
,
 .
.
,
,
- компланарны
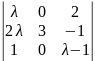 = 0 3
= 0 3 = 0
= 0
2 - - 2 = 0 1 = - 1, 2 = 2.
