1.3. Достаточный признак Вейерштрасса (равномерной сходимости функционального ряда).

_{Теорема (признак) Вейерштрасса. Если элементы функционального ряда}

_(7.8)

_{таковы, что всюду в сегменте [a,b] выполняются неравенства}

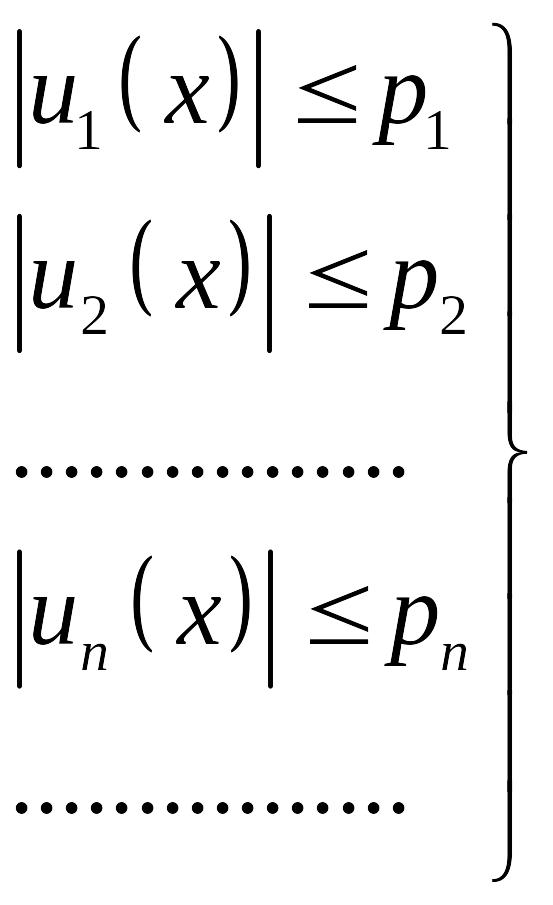_(7.9)

_{и числовой ряд с положительными членами}

_(7.10)

_{сходится, то тогда ряд (7.8) сходится в [a,b] равномерно и абсолютно.}

_{Доказательство. Пусть числовой ряд (7.10) сходится к числу L, т.е. . Тогда для любого, сколь угодно малого числа ε > 0 можно указать такое натуральное число N, чтобы при всех n > N выполнялось неравенство или с учетом того, что , неравенство}

_(7.11)

_{Теперь, рассмотрим остаток ряда (7.8) . Находим, что . Но в согласии с (7.9) получаем, что}

_(7.12)

_{при всех n > N и любых x из [a,b]. Наконец из (7.11) и (7.12) заключаем, что при всех n > N и любых x из [a,b] и так как N зависит только от ε, то это означает, что ряд (7.8) сходится в [a,b] равномерно.}

_{Абсолютная сходимость ряда (7.8) в сегменте [a,b], вытекает из сходимости в [a,b] ряда}

_{. (7.13)}

_{В силу неравенства (7.9), ряд (7.10) является мажорантой для ряда (7.13) при любых x из [a,b] и так как мажоранта сходится, то по признаку, основанному на сравнении двух положительных рядов, ряд (7.13) также сходится в [a,b], а это означает, что ряд (7.8) абсолютно сходится в [a,b]. Теорема доказана.}

_{Пример. Используя признак Вейерштрасса, докажем, что ряд}

_(7.14)

_{сходится в интервале равномерно и абсолютно.}

_{Действительно, так как то при любых действительных значениях x выполнены неравенства}

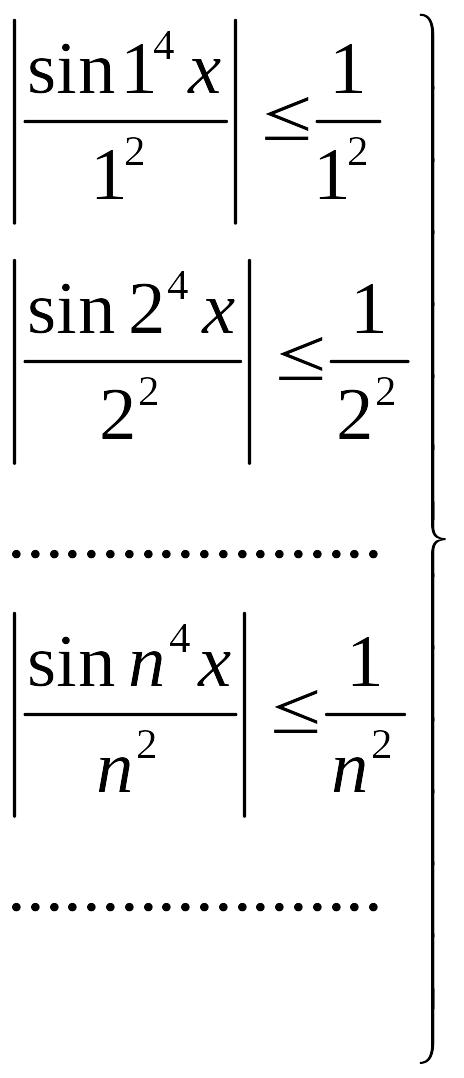
_{Далее, так как ряд сходится, то выполнены все условия признака Вейерштрасса и потому ряд (7.14) в интервале (−∞,+∞) сходится равномерно и абсолютно.}

§2. Непрерывность суммы функционального ряда

_{Теорема (о непрерывности суммы функционального ряда). Для непрерывности суммы S(x), сходящегося функционального ряда}

_(7.15)

_{в сегменте [a,b], достаточно, чтобы в этом сегменте:}

_{1) элементы ряда были непрерывными функциями;}

_{2) ряд (7.15) сходился равномерно.}

_{Доказательство. Возьмем произвольное значение x = x0 из сегмента [a,b] и докажем, что S(x) непрерывна при этом значении x.}

_{Введем обычные обозначения}

_.

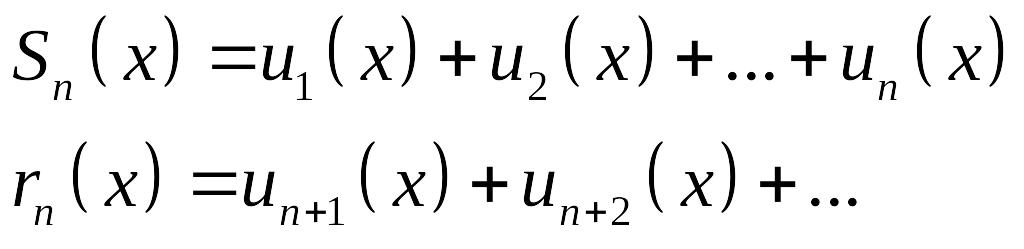_{Тогда имеем равенство . Полагая здесь x = x0, и вычитая полученное равенство из S(x) приходим к равенству}

_{, или при переходе к абсолютным значениям}

_{. (7.16)}

_{Зададим произвольно малое число ε > 0. Равномерная сходимость ряда (7.15) в сегменте [a,b] означает, что можно найти такое натуральное число N, зависящее только от ε и, следовательно, одинаковое для всех x из [a,b], что для всех n > N выполнено неравенство}

_(7.17)

_{Из изложенного следует, что выполнено также неравенство}

_(7.18)

_{После этого выбираем любое n > N и фиксируем это n.}

_{Функция Sn(x) непрерывна в [a,b], как сумма конечного числа непрерывных в этом промежутке функций. Потому по ε можно найти такое число δ > 0, зависящее от ε, что для всех x, удовлетворяющих неравенству выполнено неравенство}

_(7.19)

_{Затем считаем, что в неравенстве (7.16) n > N и , тогда, с учетом (7.17), (7.18) и (7.19), получаем, что .}

_{Таким образом, для всякого, как угодно малого, ε > 0 можно указать такое δ > 0, зависящее от ε, что, при , выполнено неравенство а это означает, что S(x) непрерывна в точке x = x0. Но так как точка x = x0 выбиралась в [a,b] произвольно, то этим доказана непрерывность S(x) всюду в [a,b].}