6.3. Степенной ряд комплексных чисел

Рассмотрим степенной ряд в комплексной Z-плоскости

. (7.134)

Здесь С₀,С₁,С₂,…,С_n,…, а также число а комплексные постоянные, а z переменное изменяющееся в комплексной плоскости.

Теорема Абеля, доказанная для степенных рядов в действительной области, может быть распространена и на ряды вида (7.134).

Сначала докажем теорему Абеля для степенных рядов в комплексной плоскости, имеющих более простой вид С₀+С₁z+C₂z²+…+C_nzⁿ+….

Теорема Абеля. Если степенной ряд

С₀+С₁z+C₂z²+…+C_nzⁿ+… (7.135)

сходится в точке z = ξ, (ξ ≠ 0) комплексной Z-плоскости, то этот степенной ряд сходится и притом абсолютно для всех z, которые удовлетворяют неравенству

. (7.136)

Геометрически это означает, что если ряд (7.135) сходится в точке z = ξ комплексной Z-плоскости (рис.83), то он сходится и притом абсолютно в каждой точке z, лежащей внутри окружности с центром в точке О начала координат и радиусом, равным .

Далее неравенство (7.136) означает, что для фиксированного z всегда можно найти такое положительное число q (0 < q < 1), что

. (7.138)

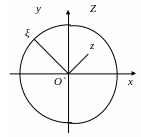
Рис. 83

Теперь для ряда (7.135) составим ряд из модулей или, что то же самое,

. (7.139)

Подставляя сюда из (7.138) получаем или немного иначе

(7.140)

Для ряда с положительными членами (7.140) в силу неравенства (7.137) ряд

M + Mq + Mq² +…+ Mqⁿ +… (7.141)

является мажорантой. Но ряд (7.141) сходится, так как получен из геометрической прогрессии 1+ q + q² +…+ qⁿ +…, знаменатель которой q удовлетворяет неравенствам 0 < q < 1 умножением всех его членов на число M > 0. Из сходимости ряда (7.141) следует, что сходится ряд (7.140). Но ряд (7.140) в свою очередь является сходящейся мажорантой ряда (7.139) и, следовательно, ряд (7.139) также сходится. Сходимость ряда (7.139) при выполнении условия (7.138) означает, что ряд (7.135) сходится и при том абсолютно для всех z удовлетворяющих неравенству (7.136). Теорема Абеля доказана.

Следствие из теоремы Абеля. Если степенной ряд (7.135) расходится в точке z = η комплексной плоскости, то он расходится для всех z, удовлетворяющих неравенству

Геометрически это означает, что степенной ряд (7.135) расходится на комплексной плоскости всюду вне окружности с центром в начале координат и радиусом .

Действительно, если бы в какой-нибудь точке z = z*, лежащей вне окружности, ряд (7.135) сходился, то он сходился бы, по теореме Абеля всюду внутри окружности с центром в начале координат и радиусом . Но тогда точка η лежит внутри этой окружности, а потому вопреки условию, ряд в точке z = η сходится и даже абсолютно. Противоречие получилось вследствие неправильного предположения о том, что хотя бы в одной точке вне окружности с центром в начале координат и радиусом , т.е. в точке z, для которой выполняется неравенство ряд (7.135) сходится. Значит для всех z, удовлетворяющих неравенству ряд (7.135) расходится.

Далее рассуждаем, так же как и в действительной области. Разбиваем степенные ряды на три типа. Степенной ряд C₀+C₁z+C₂z²+…+C_nzⁿ+… называется степенным рядом:

а) первого типа, если он сходится только при z = 0, а при всех остальных значениях z он расходится;

в) второго типа, если при некоторых значениях z ≠ 0 он сходится, но существуют такие конечные значения z, при которых он расходится;

c) третьего типа если он сходится при всех значениях z.

Теперь введем понятие круга сходимости и радиуса сходимости степенного ряда второго типа.

Определение. Кругом сходимости степенного ряда второго типа называется круг К на комплексной Z-плоскости с центром в точке z = 0 и радиусом R > 0, внутри которого степенной ряд сходится, а вне К этот ряд расходится. Радиус R круга сходимости называется радиусом сходимости степенноного ряда. На окружности круга сходимости К ряд может сходится и расходится.

Сходными рассуждениями, как и в случае действительной области, устанавливаем существование круга сходимости для степенных рядов первого и третьего типов: кругом сходимости степенного ряда первого типа является точка z = 0, а его радиус сходимости R = 0; для степенного ряда третьего типа считаем, что R = +∞, а кругом сходимости в этом случае является вся Z-плоскость.

Замечание. При рассмотрении степенных рядов общего вида

все отличие будет состоять в том, что центр круга сходимости будет находиться не в точке z = 0, а в точке комплексной Z-плоскости.

Пример 1. Исследуем сходимость ряда

. (7.142)

Составим ряд из модулей членов этого ряда

. (7.143)

Пусть z ≠ 0 (в точке z = 0 ряд сходится) и применим для исследования сходимости этого ряда с положительными членами признак Даламбера. Здесь . Отсюда

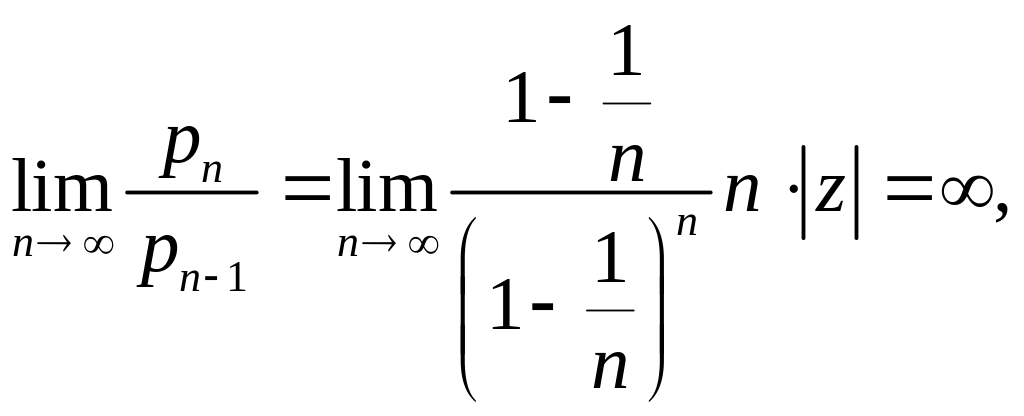
а потому оба ряда (7.142) и (7.143) при любых z ≠ 0 расходятся. Значит (7.142) есть степенной ряд первого типа.

Пример 2. Рассмотрим степенной ряд

. (7.144)

Составим для него ряд из модулей членов ряда (7.144)

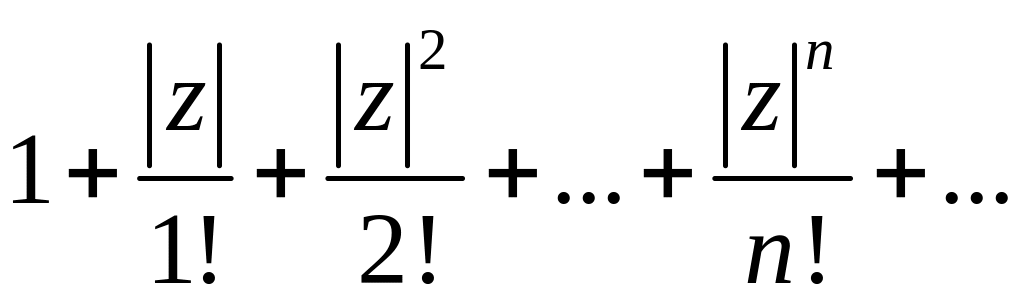. (7.145)

Далее к ряду (7.145) применим признак Даламбера. Здесь имеем

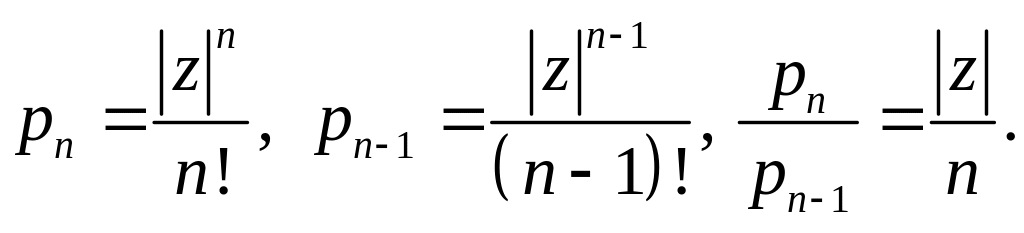Поэтому .

Отсюда можно заключить о сходимости ряда (7.144) всюду в Z-плоскости. Таким образом, (7.144) есть степенной ряд третьего типа.