§6. Ряды с комплексными членами

6.1. Предел последовательности комплексных чисел

Понятия предела последовательности действительных чисел без существенных изменений можно распространить на тот случай, когда члены последовательности суть комплексные числа.

Определение. Комплексное число а, есть предел последовательности комплексных чисел

(7.121)

и это сокращенно записывают следующим образом

(7.122)

если для всякого как угодно малого числа ε > 0, можно указать такое натуральное число N, выбор которого зависит от ε, что для всех n > N выполнено неравенство

(7.123)

Геометрически значение этого определения следующее. Построим в комплексной плоскости окружность с центром в точке а и с радиусом ε. Далее элементы последовательности (7.121) изобразим в виде точек на этой комплексной плоскости. Тогда, имея ввиду, что есть длина отрезка, соединяющего точки а и z_n, предельное равенство (7.122) означает, что как бы мало ни было число ε > 0, внутри окружности лежит бесконечное число элементов последовательности (7.121) – все те z_n, номер которых n больше N, а вне и на самой окружности лишь конечное число элементов (7.121) – либо все z₁, z₂, …, z_N, либо часть из них.

Выделяя в каждом элементе последовательности (7.121) действительную и мнимую части, представим ее в виде

x₁+iy₁, x₂+iy₂,…, x_n+iy_n,… (7.124)

и, кроме того, пусть (α и β действительные числа). В этом случае предельное равенство (7.122) принимает вид

. (7.125)

Разделяя последовательность комплексных чисел (7.124) на две последовательности с действительными аргументами x₁, x₂,…, x_n,… и y₁, y₂,…, y_n,… получаем, что предельное равенство (7.125) равносильно двум предельным равенствам , .

Это дает основание утверждать, что для последовательностей с комплексными элементами сохраняются следующие теоремы о пределах

, (с – комплексная постоянная),

,

,

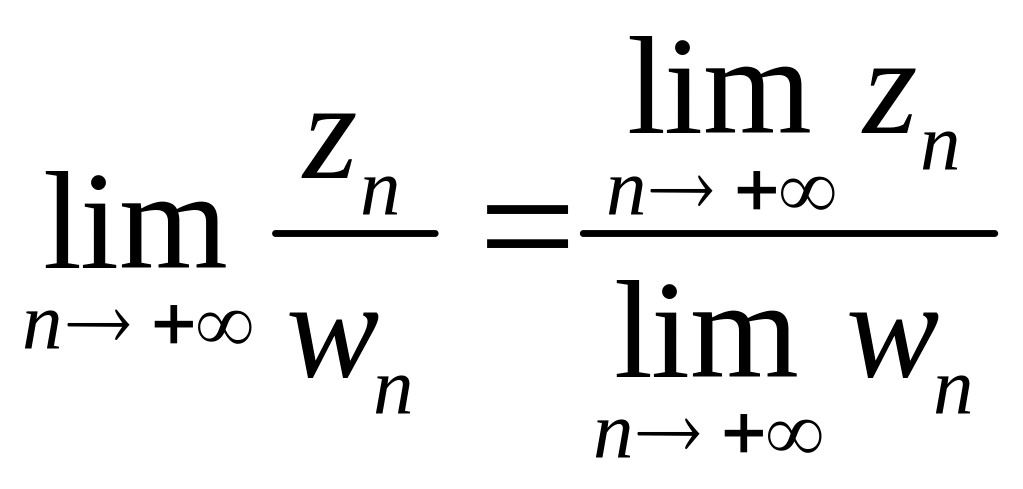(все w_n ≠ 0 и ).

Теорема Гурьева о трех последовательностях (гл.1, §5, п.5.2, теорема 4) не может быть применена, так как для комплексных чисел нет понятий «меньше» и «больше».

6.2. Сходимость ряда комплексных чисел

Рассмотрим ряд с комплексными членами

z₁+z₂+…+z_n+…. (7.126)

Как и прежде введем понятие усеченной суммы порядка n (n = 1, 2,…) S_n=z₁+z₂+…+z_n и ряду (7.126) будем ставить в соответствие последовательность усеченных сумм

S₁, S₂,…, S_n,…. (7.127)

Определение 1. Если последовательность усеченных сумм (7.127) для ряда комплексных чисел (7.126) имеет конечный предел, равный комплексному числу S: то ряд (7.126) называется сходящимся, а число S называется суммой этого ряда и записывается S = z₁+z₂+…+z_n+…. Во всех остальных случаях ряд (7.126) называется расходящимся и суммы не имеет.

Определение 2. Ряд с комплексными членами (7.126) называется абсолютно сходящимся, если сходится ряд, составленный из модулей членов ряда (7.126)

. (7.128)

Рассмотрим достаточный признак сходимости ряда (7.126).

Теорема. Для сходимости ряда (7.126) достаточно, чтобы он был абсолютно сходящимся.

Доказательство. Выделим в каждом члене ряда (7.126) действительную и мнимую части z_n = x_n+iy_n, (n = 1, 2,…) причем x_n и y_n действительные числа, тогда ряд (7.126) можно записать в виде (x₁+iy₁)+(x₂+iy₂)+…+(x_n+iy_n)+…+ и разделить его на два ряда с действительными членами

x₁+ x₂+…+ x_n+…, (7.129)

y₁+ y₂+…+ y_n+…, (7.130)

а сходящийся ряд (7.128) представить в виде

. (7.131)

Как отмечалось сходимость ряда (7.126) равносильна сходимости обоих рядов (7.129) и (7.130). Поэтому нужно доказать, что ряд (7.129) и (7.130) сходятся. Составим ряды из абсолютных величин членов рядов (7.129) и (7.130)

, (7.132)

. (7.133)

По предположению, ряд (7.131) сходится. Из очевидных неравенств

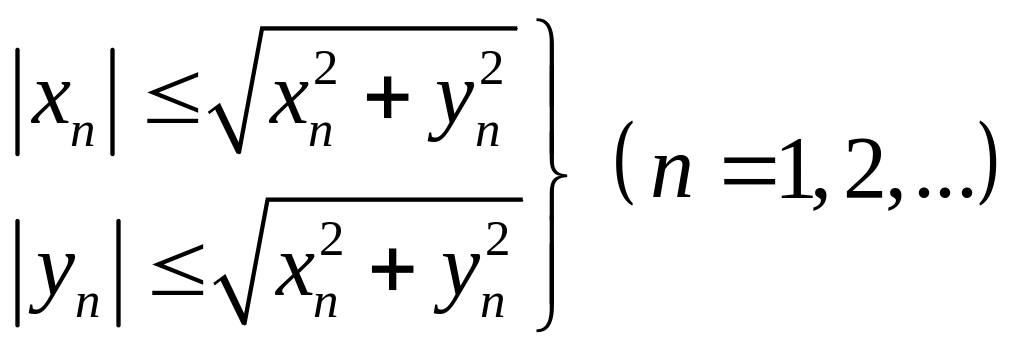
следует, что сходящийся ряд с положительными членами (7.131) является мажорантой для ряда с положительными членами (7.132) и для ряда с положительными членами (7.133). Это означает, что ряды (7.132) и (7.133) также сходятся. Отсюда, в свою очередь следует сходимость рядов (7.129) и (7.130), а соответственно и сходимость ряда (7.126). Теорема доказана.