5.5. Разложение в ряд Маклорена функции arctgx

Здесь исходной будет сходящаяся в интервале (–1,+1) геометрическая прогрессия

. (7.98)

Пусть x – произвольная точка из интервала (–1,+1): –1 < x <+1. Рассмотрим сегмент [0,x] (или [x,0], если x < 0), который целиком лежит в интервале (–1,+1) и потому, равенство (7.98) можно почленно интегрировать.

В результате несложных интегрирований получаем

. (7.99)

Ряд в правой части (7.99), также как и исходный ряд в правой части (7.98), имеет радиус сходимости равный единице. Поэтому вне сегмента [–1,+1], разложение (7.99) не действительно. Остается проверить справедливость (7.99) в точках x = +1 и x = –1. В силу нечетности обеих частей равенства (7.99) достаточно установить его справедливость при x = +1.

Заменяя в разложении (7.88) x через x², получаем

. (7.100)

Интегрируя почленно в сегменте [0,1] последнее равенство, находим

.

Отсюда, после вычисления интегралов имеем

. (7.101)

Исследуем остаточный член формулы (7.101)

(7.102)

Из последнего равенства получаем .

Отсюда следует

. (7.103)

Таким образом, в точке х = +1 функция arctg x аналитическая и для нее в этой точке имеет место разложение

. (7.104)

Из (7.104) следует, что разложение (7.99) справедливо при x = +1. В силу нечетности левой и правой части (7.99) справедливость (7.104), а, следовательно, и разложения (7.99) распространяется и на точку x = –1.

Итак, равенство (7.99) выполняется при .

Рассмотрим, как можно использовать разложение (7.99) для вычисления числа π. Для этого обозначим через φ такой угол, что

(7.105)

После этого найдем tg 2φ и tg 4φ:

; .

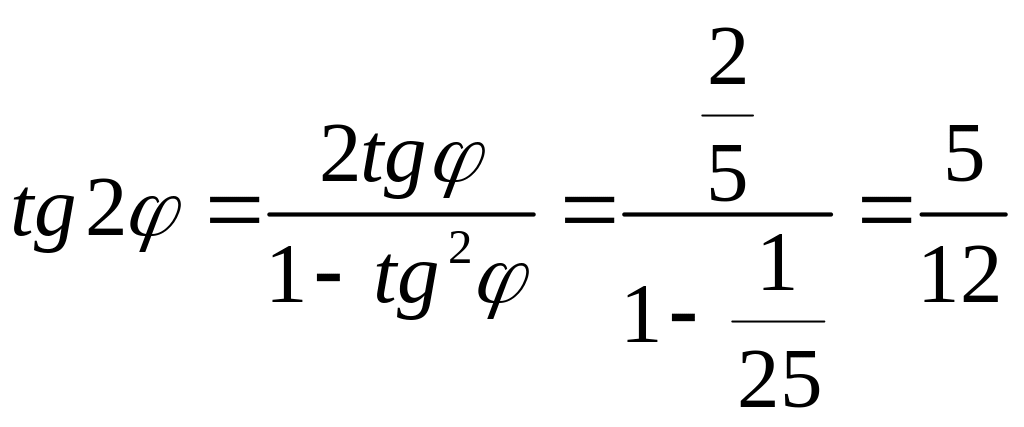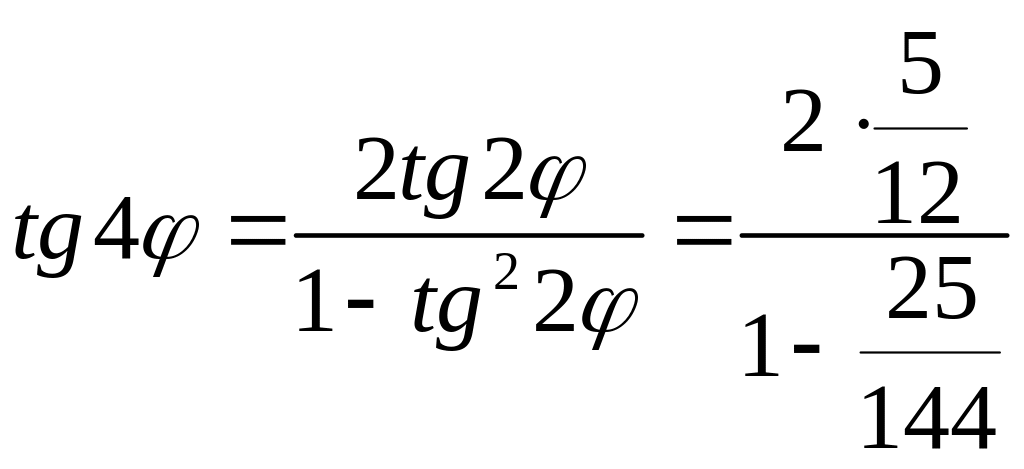
Для tg 4φ получилось значение, которое мало отличается от единицы. Поэтому 4φ незначительно отличается от . Обозначим разницу через :

(7.106)

и вычислим tg ψ

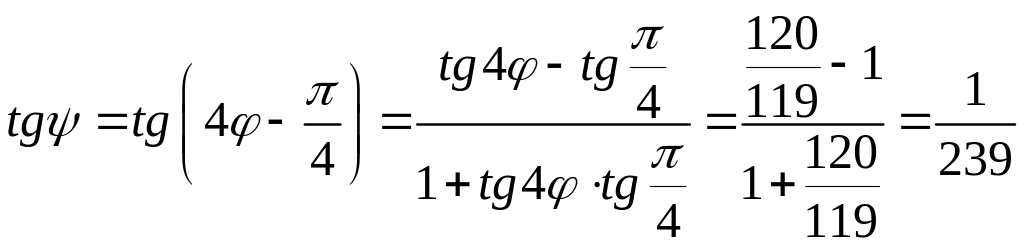. (7.107)

Из (7.105) и (7.107) находим .

Подставляя эти значения в (7.106), получаем

. (7.108)

Полагая в (7.99) и , находим

, (7.109)

. (7.110)

Отметим, что ряды в правых частях равенств (7.109) и (7.110) быстро сходятся и, следовательно, их очень удобно использовать для приближенного вычисления. Подставляя эти ряды в равенство (7.108), получим формулу для приближенного вычисления числа π

. (7.111)

Если в формуле (7.111) принять в расчет только выписанные члены рядов, то допущенную при таком вычислении ошибку ρ легко оценить.

По следствию из принципа Лейбница, при вычислении сумы ряда (7.109) с помощью первых четырех членов ряда допускается ошибка, которая меньше, чем первый отброшенный член . При вычислении суммы ряда (7.110), когда ее полагают равной первым двум членам, возникает ошибка, которая меньше, чем третий отброшенный член .

На основании изложенного ошибка ρ меньше, чем

.

Следовательно, ошибка при вычислении числа π по приближенной формуле составляет 0 < ρ <·10⁻⁶. Если в этой формуле вычисление каждого слагаемого вести до седьмого десятичного знака, то получим, причем верными являются, лишь первые пять десятичных знаков.

_{5.6. Разложение в ряд Маклорена функции (1+x)}^α

Для разложения в ряд Маклорена функции

(7.112)

где α – произволное действительное число будем пользоваться формулой Маклорена с остаточным членом R_n+1(x) в форме Коши (глава 3, §5, п.5.2, формула (3.50), при условии, что х₀ = 0)

, (7.113)

где 0 < θ < 1. Найдем последовательные производные функции (7.112)

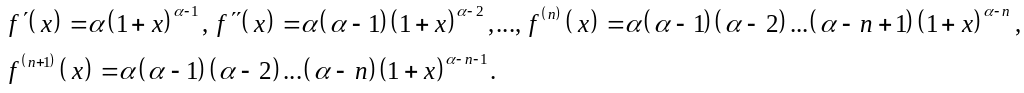
Отсюда получаем

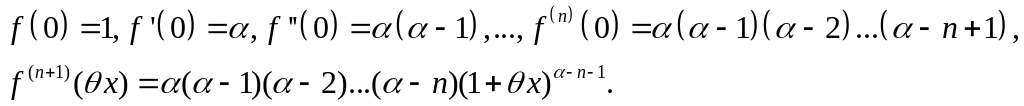
Подставляя найденные значения в (7.113), приходим к равенству

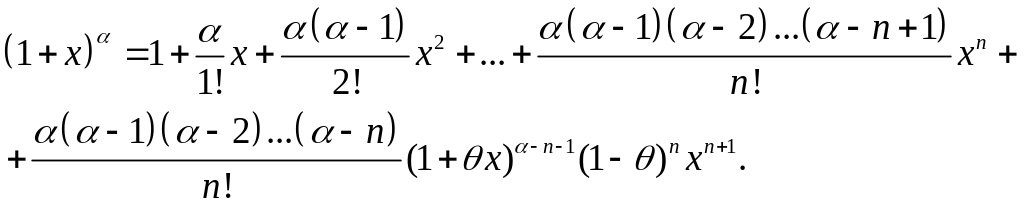(7.114)

Если α есть натуральное число: α = n, то остаточный член в (7.114), содержащий множитель α – n, обращается в нуль и в этом случае равенство (7.114) превращается в бином Ньютона

Поэтому в дальнейшем полагаем, что α ≠ 0, 1, 2,… и исследование равенства (7.114) для этих α начнем с определения радиуса сходимости R степенного ряда

. (7.115)

Для этого применим формулу .

Здесь .

Значит 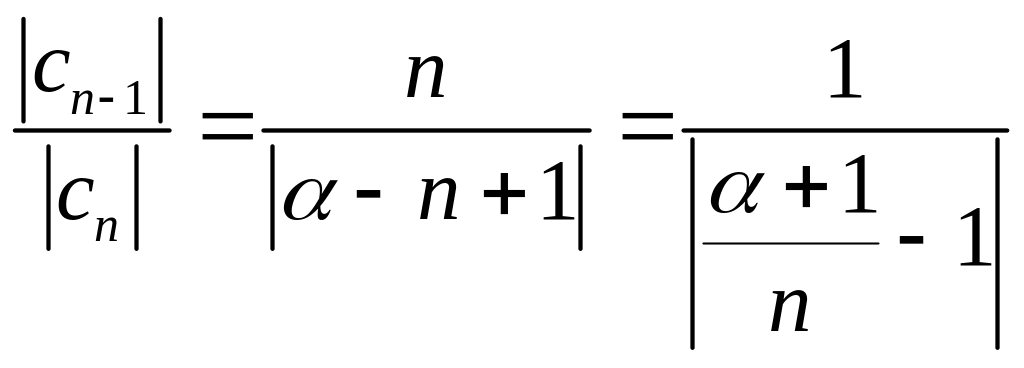и, следовательно,

.

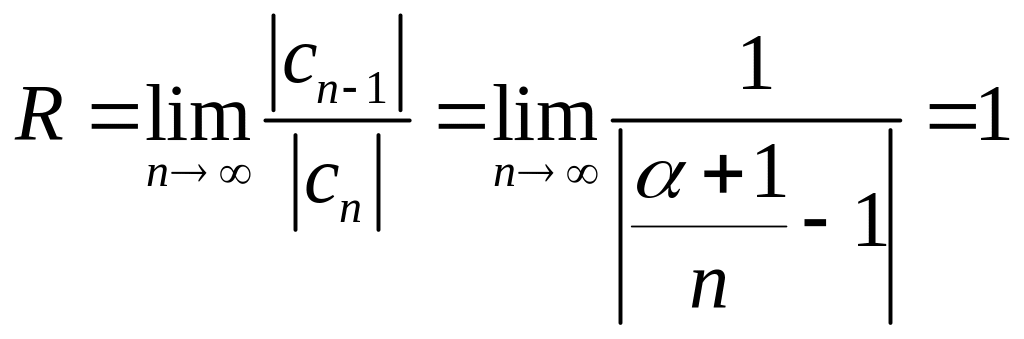Таким образом, степенной ряд (7.115) сходится при –1 < x < +1 и расходится при . Поэтому в дальнейшем считаем

–1 < x < +1. (7.116)

Для исследования остаточного члена в равенстве (7.114)

где 0 < θ < 1,

представим его несколько иначе

. (7.117)

Теперь рассмотрим по отдельности поведение всех трех сомножителей в правой части (7.117): и при n→+∞.

Радиус сходимости степенного ряда (7.115) не зависит от величины параметра α, поэтому, если в (7.115) заменить α через α – 1, то степенной ряд

(7.118)

также имеет радиус сходимости равный 1. Это означает, что для всех х в интервале –1 < x <+1 общий член ряда (7.118) при n → +∞ имеет своим пределом число нуль

. (7.119)

При соблюдении неравенства (7.116) имеем и отсюда .

Множитель αx(1+θx)^α-1 остаточного члена (7.117) зависит от n, так как θ зависит и от x и от n. Но этот множитель ограничен, так как при любых значениях n он находится между величинами αx и αx(1+x)^α-1, которые от n не зависят.

Таким образом, первый множитель остаточного члена R_n+1(x) в формуле (7.117) для всех х из интервала (–1,1) при n→+∞ в силу (7.119) имеет своим пределом нуль, а второй и третий множитель ограничены. Поэтому для всех х из интервала (–1,1) выполняется предельное равенство .

Следовательно, функция (7.112) в точке х = 0 аналитическая и для нее в интервале (–1,1) справедливо разложение

. (7.120)

Ряд в правой части (7.120) называется биномиальным рядом.

Рассмотрим частные случаи разложения функций с использованием биномиального ряда.

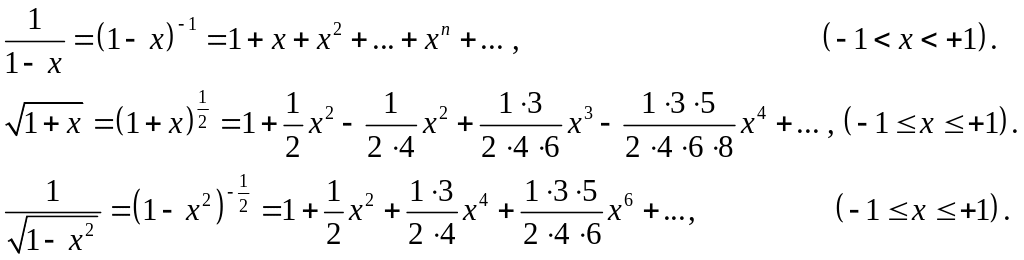
Интегрируя последнее разложение в сегменте [0,x], получаем

.

В заключение приводится таблица, показывающая характер сходимости биномиального ряда на концах интервала сходимости.

	х = –1		х = +1
α ≥ 0	АБСОЛЮТНО СХОДИТСЯ	α ≥ 0	АБСОЛЮТНО СХОДИТСЯ
α <0	РАСХОДИТСЯ	–1<α<0	НЕАБСОЛЮТНО СХОДИТСЯ
		α ≤ –1	РАСХОДИТСЯ

Биномиальный ряд, в частности, может быть использован для вычисления корней с любой наперед заданной степенью точности. Пусть, например, нужно вычислить . Последовательно получаем

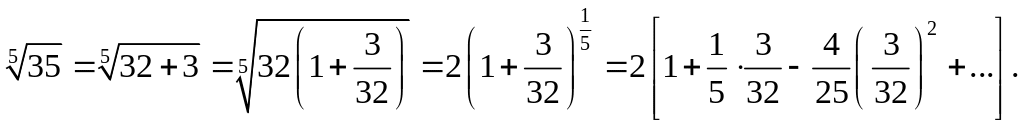
Беря нужное число членов получившегося ряда, смотря по требуемой степени точности, вычисляем приближенное значение .