5.3. Разложение в ряд Маклорена функций sin X, cos X

_{Сначала разложим функцию sin x в ряд Маклорена. Для этого в основу кладется формула Маклорена, которую удобно записать в более подробной форме}

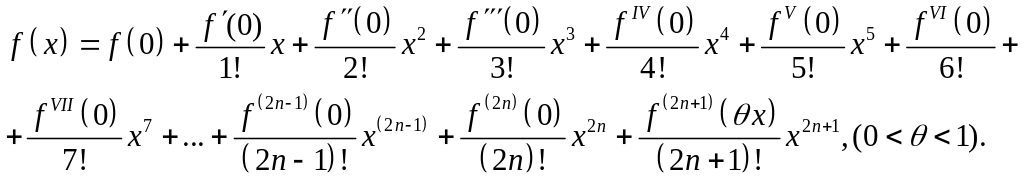_(7.82)

_{Положим здесь f(x) = sin x. Последовательное дифференцирование дает}

_{Отсюда находим}

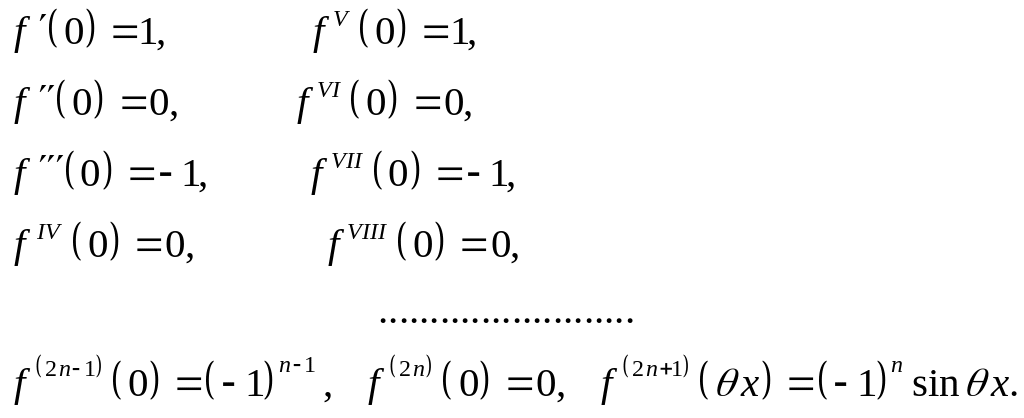
_{Подставляя эти значения в (7.82), получим}

. (7.83)

Остаточный член при n стремится к пределу 0. Действительно, последовательность 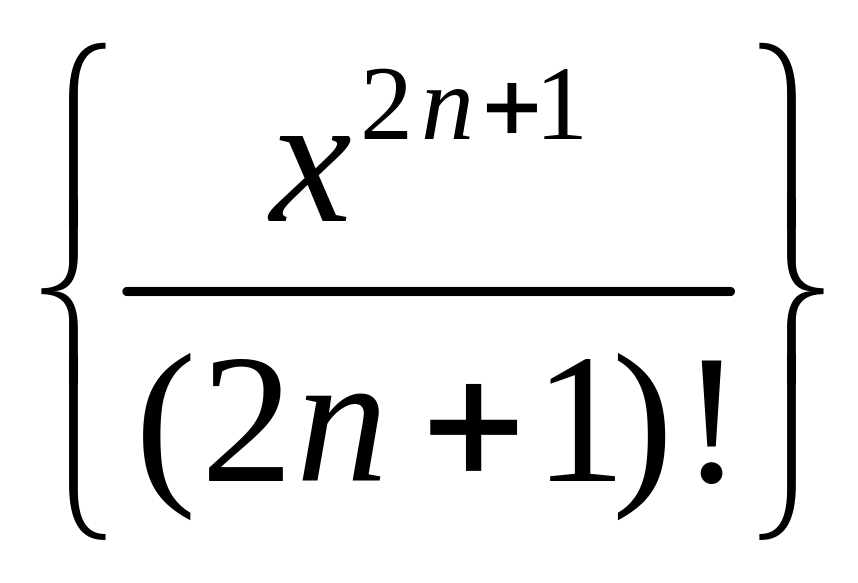является подпоследовательностью последовательности , которая при n (см. предельное равенство (7.76)) стремится к пределу 0, следовательно, имеем, а так как величина ограниченная, то .

Тот факт, что для функции sin x в формуле Тейлора (7.83) , согласно теореме 1, §5, п.5.1 означает, что функция sin x в точке х = 0 аналитическая и для нее справедливо разложение

. (7.84)

Аналогичными рассуждениями доказываем, что

. (7.85)

Почленное дифференцирование разложений (7.84) и (7.85) дает

, .

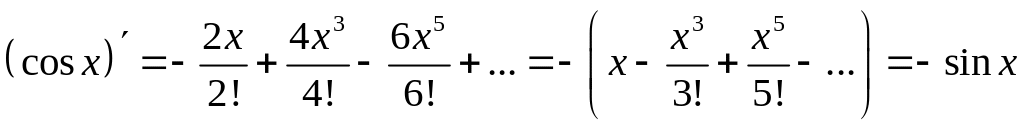Следовательно, этим подтверждается, что при дифференцировании разложений (7.84) и (7.85) равенство сохраняется.

_{5.4. Разложение в ряд Маклорена функции ln(1+x)}

Исходим из того, что в интервале (–1,1) справедливо разложение

. (7.86)

Степенной ряд в правой части есть сходящаяся геометрическая прогрессия, знаменатель которой равен –x, а интервалом сходимости его служит (–1,1). Далее считаем и рассмотрим сегмент [0,x] (или [x,0], если x < 0). Этот сегмент целиком лежит в интервале сходимости степенного ряда, а тогда, равенство (7.86) можно интегрировать почленно. В результате получаем

.

Выполняя несложные интегрирования, получим после упрощений

. (7.87)

Справедливость этого разложения установлена для , а поскольку, при почленном интегрировании сходящегося ряда, его радиус сходимости не изменяется (§4, п.4.3), поэтому ряд в правой части равенства (7.87) имеет тот же радиус сходимости, что и исходный степенной ряд в правой части равенства (7.86), т.е. R = 1. Это означает, что степенной ряд в правой части равенства (7.87) вне сегмента [–1,1] расходится, а потому остается исследовать разложение (7.87) в точках x = ±1. Ряд, полученный в правой части равенства (7.87) после подстановки в него x = –1 является расходящимся гармоническим рядом все члены, которого умножены на –1

.

Поэтому в точке x= –1 равенство (7.87) не выполнено.

В точке x = +1 в правой части разложения (7.87) получается полугармонический ряд который, по признаку Лейбница, сходится. Докажем, что его суммой является ln2, и, следовательно, равенство (7.87) соблюдается в точке x = +1.

Из двух тождеств

и

выводим новое тождество .

Деля обе части на 1+x, получаем

. (7.88)

Интегрирование этой конечной суммы в сегменте [0,1] дает

. (7.89)

Оценим остаточный член

Сначала имеем

. (7.90)

Уменьшим знаменатель подинтегральной функции (7.90), заменяя 1+ x через x. Это приведет к увеличению правой части (7.90) и тогда получим неравенство

.

Итак, и отсюда заключаем, что

. (7.91)

Это означает, что функция в точке х = +1 аналитическая и равенство (7.89) может быть заменено на равенство (7.87) если в нем положить х = +1

. (7.92)

Теперь окончательно приходим к выводу, что разложение (7.87)

справедливо в полусегменте .

Дальше рассмотрим практическое использование разложения (7.87) для вычисления логарифмов натуральных чисел.

Для функции ln(1 – x) разложение в ряд Маклорена получается из (7.87) заменой x через –x

(7.93)

справедливо при .

Вычитая из (7.87) равенство (7.93), получим

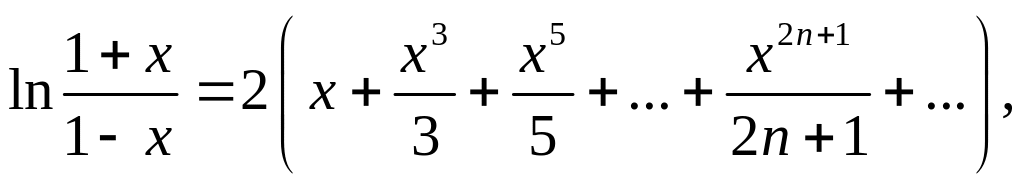(7.94)

причем ряд в правой части сходится в интервале (–1,+1).

Пусть m – натуральное число m = 1, 2,… и положим

. (7.95)

При указанных значениях для m справедливо неравенство

и потому, при таком значении x разложение (7.94) остается справедливым.

Подставляя (7.95) в (7.94), получим после упрощений

(7.96)

Равенство (7.96) ввиду быстрой сходимости ряда в правой части этого равенства является наиболее удобным для приближенного вычиления логарифмов натуральных чисел. Рассмотрим некоторые примеры такого вычисления.

Полагая в (7.96) m = 1, получим

. (7.97)

Для приближенного вычисления ln2 ограничемся первыми пятью членами данного разложения = 0,69314.

Ошибка ρ такого приближенного вычисления равна

.

Ряд в скобках есть сходящаяся геометрическая прогрессия со знаменателем и его сумма равна и потому . Отсюда можно заключить об эффективности использования разложения (7.97) для вычисления ln2, которое уже для пяти членов разложения дает ошибку меньше 10⁻⁵.

Если в (7.96) положить m = 4, то получаем .

Отсюда найдем ln5 = 1,60944....

Зная ln2 и ln5 можем найти ln10 = ln2+ln5 = 2,30258..., а также модуль перехода от натуральных логарифмов к десятичным

Полагая в (7.96) m = 80 = 2⁴·5, тогда

.

Отсюда находим ln3=1,0986 и .