5.2. Разложение в ряд Маклорена функции ex

_{Исходной является формула Маклорена}

,

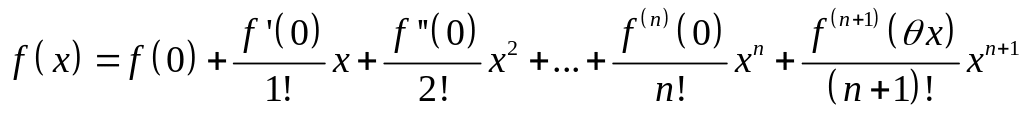_{где θ лежит в интервале (0,1). Положим здесь f(x) = e}^x _{и в результате последовательного дифференцирования находим}

_.

_{Отсюда следует, что}

_{Подставляя эти значения в формулу Маклорена, получаем}

_{. (7.74)}

_{Последнее слагаемое в правой части есть остаточный член формулы Маклорена}

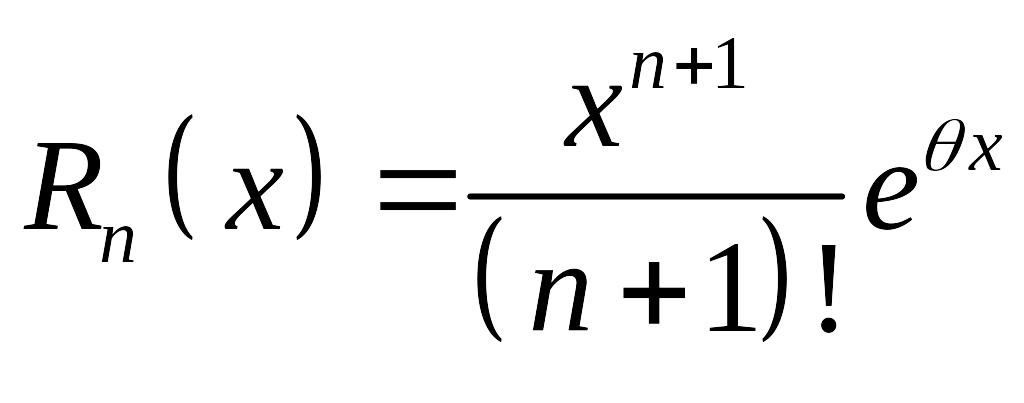_{. (7.75)}

_{Теперь для того чтобы установить является ли функция e}^x _{аналитической и для нее имеет место равенство необходимо в соответствии с теоремой 1 доказать, что остаточный член Rn(x) в формуле Маклорена (7.74) при n →+∞ стремится к нулю.}

_{Первый множитель остаточного члена (7.75) формулы Маклорена (7.74) представляет собой общий член степенного ряда , который сходится при всех значениях x (см. пример 2, §4, п.4.1.3). Поэтому общий член этого ряда при n →+∞ имеет предел равный нулю}

_{. (7.76)}

_{Второй сомножитель e}^θx _{при фиксированном х содержится между e}⁰ _{= 1 и e}^x_{, а потому ограничен. Известно, что произведение бесконечно малой величины на ограниченную величину есть бесконечно малая величина, следовательно}

_{при .}

_{Отсюда, в силу достаточности условий, теоремы 1 функция e}^x _{является аналитической и для нее следует справедливость равенства}

_{. (7.77)}

_{На рис.82 пунктиром изображен график показательной функции y = e}^x _{и сплошными линиями – графики усеченных сумм ее маклореновского разложения}

_{Рис. 82}

_{Как видно из рис.82 с увеличением порядка усеченной суммы ее график в окрестности точки x = 0 все более плотно приближается к графику показательной функции y = e}^x_{. Ясно, что график n-ой усеченной суммы}

_{при n →+∞ практически превратится в график функции y = e}^x_.

_{Рассмотрим некоторые применения равенства (7.77):}

_{1) В результате дифференцирования равенства (7.77) находим}

_{После упрощений в правой части, получаем . Итак . Таким образом, равенство (7.77) можно дифференцировать и равенство при этом сохраняется.}

_{2) Заменяя в равенстве (7.77) x на x – a, имеем}

_или

_{. (7.78)}

_{Согласно теореме 3 о единственности разложения функции в ряд Тейлора, последний степенной ряд является рядом Тейлора по степеням x – a для e}^x_.

_{3) Используя тождество разложение (7.77) и теорему 3 о единственности разложения, получаем разложение в ряд Маклорена функции a}^x

_{. (7.79)}

_{Дифференцирование равенства (7.79) дает}

_.

_{Итак, получаем, что , следовательно, разложение (7.79) можно дифференцировать и равенство при этом сохраняется.}

_{4) Заменим в (7.77) x через –x и тогда}

_{. (7.80)}

_{Подставляя разложения (7.77) и (7.80) в формулы}

_{находим разложения для гиперболических функций shx и chx в ряд Маклорена}

_,

_.

_{5) Для определения численного значения числа e положим в (7.77) x = 1, получаем . Этот ряд очень быстро сходится и весьма удобен для вычисления числа е. Действительно, если приближенно положить}

_(7.81)

_{то ошибка ρ этого приближенного равенства равна}

_.

_{Заменяя все множители в знаменателях дробей внутри квадратной скобки через меньшее число n + 1, находим . Внутри квадратной скобки получилась сходящаяся геометрическая прогрессия. Находя ее сумму, получим .}

_{Итак, для ошибки ρ приближенного равенства (7.81) имеем .}

_{Например, при n = 10 приближенно полагая ,}

_{ошибка ρ, составляет .}