МІНІСТЕРСТВО ОСВІТИ УКРАЇНИ

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ТЕХНОЛОГІЙ ТА ДИЗАЙНУ

Методичні вказівки

до виконання лабораторних робіт з фізики

Розділи

“МЕХАНІКА”, “МЕХАНІЧНІ КОЛИВАННЯ ТА ПРУЖНІ ХВИЛІ”,

“МОЛЕКУЛЯРНО – КІНЕТИЧНА ТЕОРІЯ ТА

ТЕРМОДИНАМІКА”

Частина 1

Затверджено на засіданні

кафедри фізики

протокол №7 від 23.12.2004 р.

Київ – 2005

Методичні вказівки до виконання лабораторних робіт з фізики. Розділи “Механіка”, “Механічні коливання та пружні хвилі”, “Молекулярна фізика та термодинаміка”. /Упорядники А.П. Клименко, В.Ф. Лапшин, К.В. Авдонін, В.К. Максімов, Б.М. Стаднік, В.М.Годованюк – К.: КНУТД, 2005. – 53 С. Укр. мовою./

УПОРЯДНИКИ: А.П. Клименко

В.Ф. Лапшин

К.В. Авдонін

В.К. Максимов

Б.М. Стаднік

В. М. Годованюк

Підготовка до виконання лабораторної роботи

1. Написати протокол у зошиті для звітів з лабораторних робіт по дисципліні загальна фізика, в якому повинно бути:

   • тема роботи;

   • обладнання;

   • мета роботи;

   • стислі теоретичні відомості;

   • порядок виконання роботи;

   • таблиці результатів вимірювань та обчислень.

2. Повторити теорію, відповідну до теми роботи, використовуючи конспект лекцій або посібники з курсу загальної фізики.

3. Знайти відповіді на контрольні питання, мати загальне уявлення про методи вимірювання фізичних величин в даній лабораторній роботі.

Оцінка точності вимірювань фізичних величин

Всі виміри фізичних величин поділяються на два типи:

1. Прямі вимірювання – безпосередньо за допомогою приладу;

2. Опосередковані вимірювання – величина обчислюється за відомою формулою, в яку входять, як параметри, величини знайдені прямими вимірюваннями.

Нехай фізична величина, яка вимірюється. Величина має, звичайно, істинне значення , яке ми ніколи не взнаємо, оскільки будь – яке вимірювання має похибку. Наближеним до значенням величини буде середнє значення виміряних величин, яке позначимо через , точність його наближення до істинного значення оцінюється за допомогою інтервалу сподівання , який на числовій прямій можна зобразити таким чином:

Істинне значення може, як належати, так і не належати інтервалу сподівання. Позначимо через імовірність події, яка полягає в тому, що істинне значення величини належить інтервалу сподівання. Ця імовірність задається довільно і чим більше вибране значення наближається до одиниці, тим більшим повинен бути інтервал сподівання .

Знаходження середнього значення та інтервалу сподівання для прямих вимірювань.

Позначимо через фізичну величину, яка вимірюється прямим шляхом. Якщо разів її вимірювати, то в загальному випадку одержуємо різних значень цієї величини: . Послідовність обчислень, необхідних для знаходження середнього значення та оцінки точності вимірювань така:

1. Обчислити середнє значення величини, як середньоарифметичне від виміряних величин:

. (1)

2. Обчислити систематичну складову інтервалу сподівання (похибку, яка залежить від точності приладу). Позначимо її через :

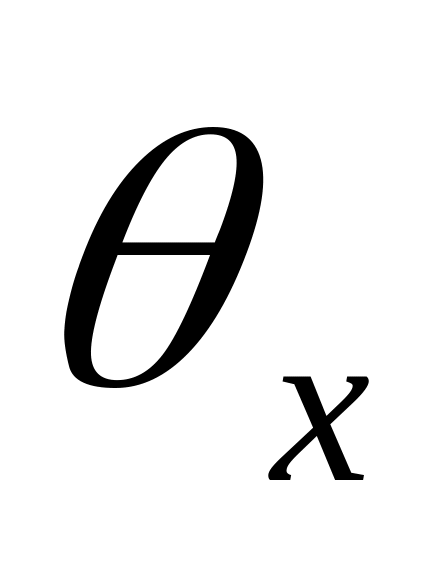(найменша поділка шкали приладу); якщо у приладу немає

класу точності;

, якщо у приладу є клас точності, який ми позначили через ,

максимальне значення величини, яку можна виміряти

приладом в даному випадку.

3. Обчислити стандартну похибку вимірювань :

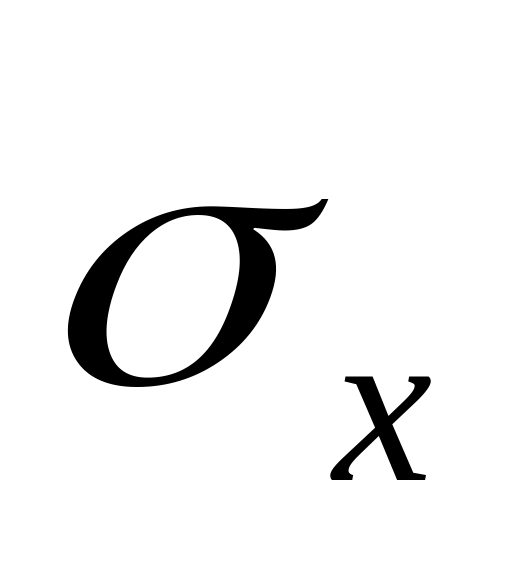; (2)

стандартна похибка є характеристикою випадкової складової інтервалу сподівання.

4. Порівняти між собою систематичну та випадкову складові інтервалу сподівання, для цього знаходимо безрозмірне число 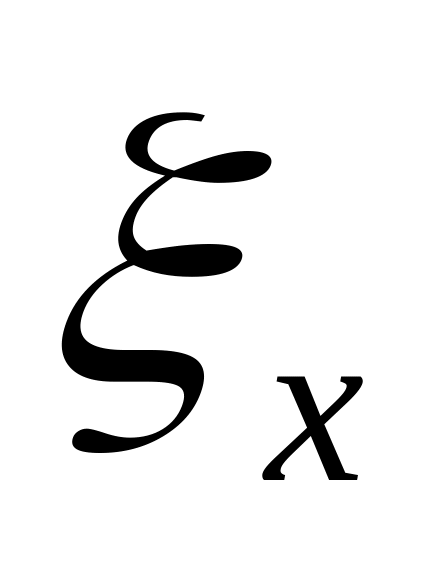, яке дорівнює відношенню:

(3)

5. Обчислити випадкову складову інтервалу сподівання, позначивши її через :

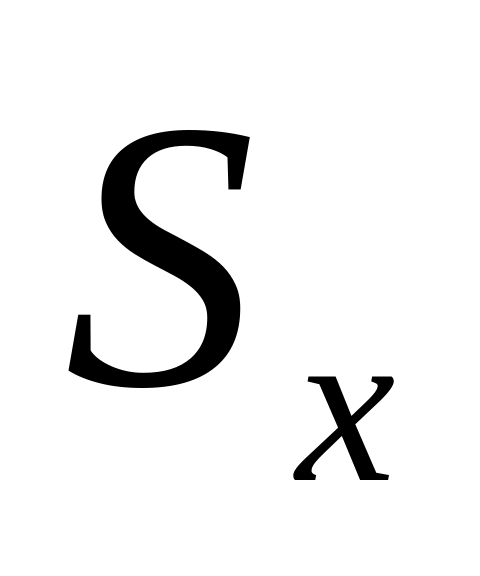(4)

де: коефіцієнт Стьюдента, параметр, який треба вибрати із таблиць, задаючись певним значенням імовірності та враховуючи кількість вимірювань . Значення коефіцієнтів Стьюдента, які найчастіше будуть використовуватись в лабораторних роботах приведені в таблиці:

Р	
	2	3	4	5	7	10	20	40
0,68	1,9	1,26	1,2	1,14	1,08	1,05	1,03	1,01
0,95	12,7	4,4	3,13	2,78	2,45	2,26	2,09	2,02

6. Знайти інтервал сподівання для прямих вимірювань за правилами:

, якщо ;

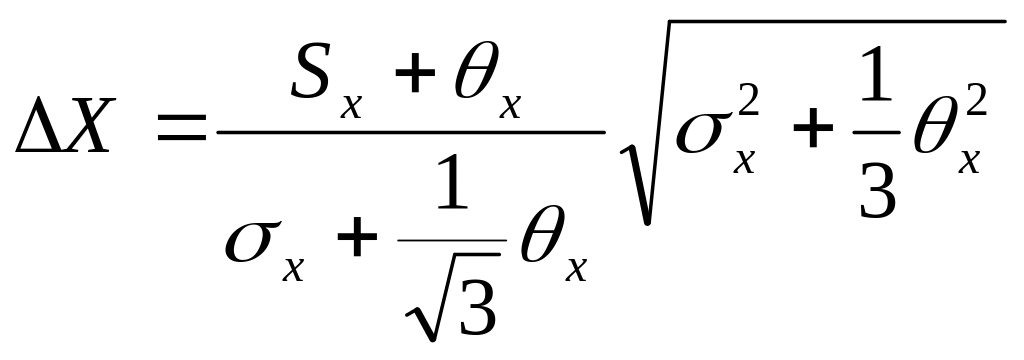, якщо ;

, якщо . (5)

Знаходження середнього значення та інтервалу сподівання опосередкованих вимірювань.

Нехай фізична величина, яку ми вимірюємо опосередкованим чином, тобто обчислюємо її за відомою формулою:

(6)

де: - величини, виміряні прямим шляхом, тоді, звичайно, можна обчислити їх середні значення та інтервали сподівання , використовуючи методику оцінки точності прямих вимірювань. Далі послідовність обчислень буде такою:

1. Знаходимо середнє значення, яке позначимо через :

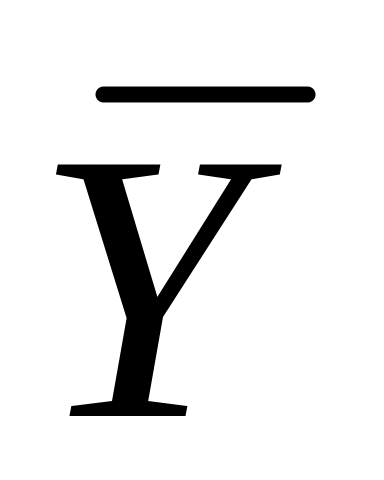(7)

2. Обчислюємо інтервал сподівання :

(8)

Спільною характеристикою точності прямих та опосередкованих вимірювань є відносна похибка вимірювань, яку ми позначимо через .Обчислюється вона, як відношення:

; (9)

Результат прямих та опосередкованих вимірювань необхідно записувати в стандартному вигляді:

; (10)

Застосування методу найменших квадратів до вимірювання фізичних величин.

Нехай нам відомо, що дві фізичні величини та , які ми вимірюємо, звязані лінійною залежністю:

, де: , які треба знайти. (11)

Результатами вимірювань будуть пари відповідних значень величин:

; (12)

кожній парі значень на координатній площині відповідає точка, як показано на рисунку 1:

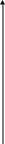
Y

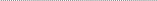
O X

Рис. 1.

Для знаходження невідомих сталих та , можна провести на координатній площині пряму, яка буде проходити якомога ближче до всіх точок, що ілюструють результати експерименту (див. рис. 1), тоді: , а параметр дорівнює координаті точки перетину прямої з віссю Y.

Метод найменших квадратів дозволяє знайти параметри лінійної залежності та інтервали сподівання для них , шляхом тільки обчислень.

а) Якщо залежність між та має вигляд: , тобто , то

послідовність обчислень буде такою:

1.Обчислити величини за формулами:

; . (13)

2. Знайти параметр , як відношення знайдених величин:

. (14)

3. Обчислити інтервал сподівання :

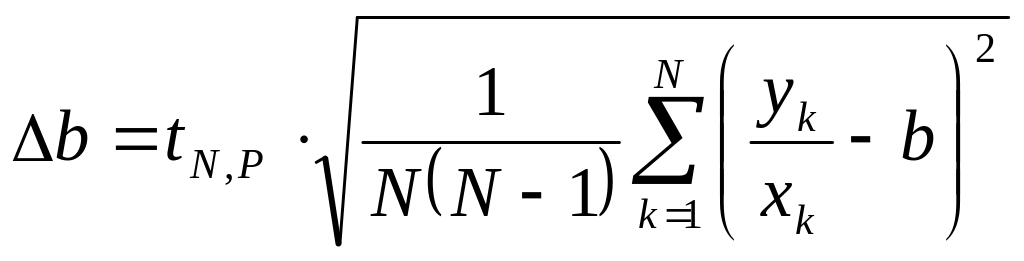. (15)

б) Якщо залежність між та має вигляд: , тобто , то

послідовність обчислень буде такою:

1. Обчислити величини , за формулами:

; ; ;

; ; . (16)

2. Обчислити коефіцієнт кореляції :

. (17)

коефіцієнт кореляції – це безрозмірне число в межах , яке

характеризує степінь взаємозвязку величин та , якщо , то всі

точки, які ілюструють результати експерименту (див. рис. 1), належать

одній прямій. Якщо , то величини та лінійно не звязані.

3. Обчислити параметри лінійної залежності і за правилами:

(18)

(19)

4. Обчислити інтервали сподівання та для параметрів:

; (20)

. (21)