14. Функція Жуковського. Так називається функція
. (1)
Оскільки
,
то функція
є голоморфною в
і є конформним відображенням в
.
Далі,
тоді і тільки тоді, коли
.
Тому
розглядувана функція є однолистою в
будь-якій області, яка не містить двох
різних точок
і
таких, що
.
Такими є, зокрема, області
і
,
та
.
Якщо
,
і
,
то
Звідси
отримуємо, що у випадку
,
,
. (2)
Отож,
коло
,
,
переходить в еліпс (2), а коло
у відрізок
,
який обходиться двічі. Тому,
,
При цьому,
Приклад
1.
Знайдемо
функцію, яка конформно і однолисто
відображає
на
півплощину
.
Для цього розглянемо функції
,
,
,
та
.
Тоді функція
є шуканою, бо
,
,
,
,
.
Приклад
2.
Знайдемо
функцію, яка конформно і однолисто
відображає
на
.
Для цього розглянемо функції
,
,
де
– голоморфна гілка в
функції, оберненої до функції Жуковського,
яка в
приймає значення
0.
Тоді функція
є шуканою, бо
,
.
Приклад
3.
Знайдемо
функцію, яка конформно і однолисто
відображає
на
.
Для цього розглянемо функції
,
,
де
– голоморфна гілка в
функції, оберненої до функції Жуковського,
яка в точці
приймає значення
.
Тоді функція
є
шуканою, бо
,
,
.
Приклад
4.
Знайдемо
функцію, яка конформно і однолисто
відображає
на
.
Для цього розглянемо функції
,
,
та
,
де
– голоморфна гілка в
функції, оберненої до функції Жуковського,
яка в
приймає значення 0. Тоді функція
є шуканою, бо
,
,
,
.
Приклад
5.
Функція
конформно і однолисто відображає півкруг
на
півплощину
.
Приклад
6.
Функція
конформно і однолисто відображає
на
так, що фіксована точка
переходить в точку
,
а функція
конформно і однолисто відображає
на
так, що точка
переходить в точку 0. Тому функція
конформно і однолисто відображає на так, що задана точка переходить в точку 0.
15. Функція . Оскільки , то функція є конформним відображенням в кожній точці . Далі,
Тому областями однолистості функції є такі області, які не містять двох різних точок і таких, що виконується принаймі одна із рівностей:
,
.
До таких областей належать зокрема півсмуги
та смуги
Оскільки
,
то функцію
можна подати як композицію чотирьох
відображень:
,
,
,
.
При цьому
Таким
чином,
,
причому відображення є конформним і
однолистим. Подібним чином можна знайти
образи областей
,
та
.
Можна міркувати й інакше. Якщо
,
і
,
то
звідки
(1)
Тому
кожна пряма
відображається на гіперболу (1), причому
на праву гілку, якщо
і ліву, якщо
.
Пряма
відображається на пряму
,
а прямі
та
на проміжки
і
.
Таким чином, функція
конформно
і однолисто відображає
на область
,
причому верхні півпрямі
відображаються на верхні береги розрізів,
а нижні – на нижні. Отже, в області
існує однозначна і голоморфна гілка
функції
,
яка конформно і однолисто відображає
на
,
причому
,
де
та гомоморфна гілка кореня в
,
яка в точці 0 приймає значення 1.
Приклад
1.
Побудуємо
конформне і однолисте відображення
півсмуги
на
.
Для цього розглянемо відображення
та
.
Тоді функція
є шуканою, бо
,
.
16. Запитання для самоконтролю.
Сформулюйте означення похідної функції та основні правила її знаходження.
Сформулюйте критерій існування похідної функції та доведіть його. Запишіть умови Коші-Рімана.
Яка функція називається конформним відображенням?
В чому полягає геометричний зміст модуля похідної функції ?
В чому полягає геометричний зміст аргумента похідної функції ?
Яку функцію називають голоморфною в точці?
Яку функцію називають голоморфною в області?
Яку функцію називають голоморфною в замкненій області?
Яку функцію називають цілою?
Яку функцію називають моногенною в точці?
Яку функцію називають лінійною?
Композицією яких відображень є лінійна функція?
На що відображає лінійна функція промінь, який виходить з початку координат, та круг з центром в початку координат?
В якій області лінійна функція є однолистим і конформним відображенням?
Яку функцію називають афінною?
Композицією яких відображень є афінна функція?
На що відображає афінна функція промінь, який виходить з початку координат, та круг з центром в початку координат?
В якій області афінна функція є однолистим і конформним відображенням?
Які точки називають симетричними відносно кола та відносно прямої?
На що відображає промінь, який виходить з початку координат, та круг з центром в початку координат?
Композицією яких відображень є функція ?
Яку функцію називають дробово-афінною?
Композицією яких відображень є дробово-афінна функція?
В якій області дробово-афінна функція є однолистим і конформним відображенням?
Сформулюйте і обґрунтуйте колову властивість дробово-афінної функції.
Обґрунтуйте спосіб побудови дробово-афінної функції за образами
трьох точок.
На що дробово-афінна функція відображає круг, зовнішність круга, півплощину?
Вкажіть області однолистості відображення
На що функція відображає круг з центром в початку координат, зовнішність круга з центром в початку координат? Чи є у вказаних областях відображення однолистим?
На яку множину функція відображає промінь з вершиною в початку координат?
На яку множину функція відображає кут з вершиною в початку координат? Коли у вказаній області відображення є однолистим?
Вкажіть області, в яких існують однозначні гілки відображення .
На що однозначна і неперервна гілка функції в області
,
яка в точці 1 приймає значення 1, відображає
півплощину
та кут
?
В яких точках відображення є конформним?
Вкажіть області однолистості відображення .
На що функція відображає смугу ?
Яка функція конформно і однолисто відображає область
на смугу
?В яких точках функція Жуковського
є конформним відображенням?Опишіть області однолистості відображення
.Вкажіть функцію, яка є конформним і однолистим відображенням півкруга на півплощину.
17. Вправи і задачі.
2.1. Знайдіть кут повороту і коефіцієнт розтягу відображення в точці :
1.
,
.
2.
,
.
3.
,
.
4.
,
.
5.
,
.
6.
,
.
7.
,
.
8.
,
.
9.
,
.
10.
,
.
2.2. В яких точках функція є голоморфною та моногенною?
1.
. 2.
.
3.
. 4.
.
5.
,
. 6.
.
7. . 8. .
9.
.
10.
.
11.
.
12.
.
13.
. 14.
.
2.3. Чи існує голоморфна в деякій точці функція , для якої:
1.
,
.
2.
,
.
3.
,
.
2.4. Знайдіть образи множини за відображення :
1.
,
.
2.
,
.
3.
,
.
4.
,
.
5.
,
.
6.
,
.
7.
,
.
8.
,
.
9.
,
.
2.5. Знайдіть образи множини за відображення :
1.
,
,
.
2.
,
,
.
3.
,
,
.
4.
,
,
.
5.
,
,
.
6.
,
,
.
7.
,
,
.
8. , , .
9.
,
,
.
2.6. Знайдіть всі афінні функції, які відображають множину на множину :
,
.,
.
,
.,
.,
.
,
.
,
.
,
.
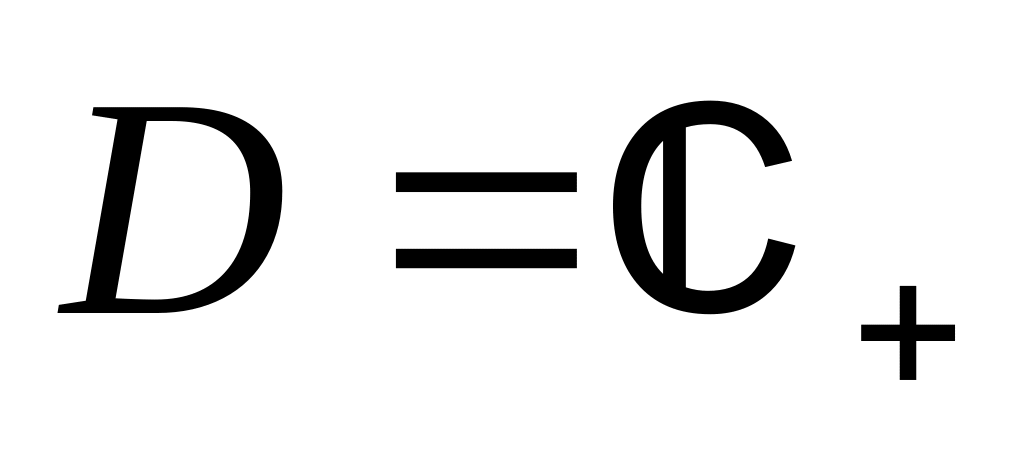2.7.
Знайдіть нерухому точку
функції
і подайте цю функцію у вигляді
:
1.
. 2.
. 3.
.
2.8. Знайдіть афінну функцію, яка відображає множину на множину :
1.
,
.
2.
,
.
2.9.
Знайдіть
або
:
1.
, 
.
2.
, 
.
3.
,
.
4.
,
.
5.
, 
.
6.
, 
.
7. , .
8. , .
9.
,
.
10.
,
.
11.
,
.
12.
, 
.
13.
,
.
14.
,
.
15.
, 
.
16.
,
.
17.
,
.
18.
, 
.
19.
,
.
20.
,
.
21.
,
.
22.
, 
.
23.
,
.
24.
,
.
25.
,
.
26.
,
.
27.
,
.
28.
,
.
29.
,
.
30.
,
.
31. , .
32.
,
.
33.
,
.
34. , .
35.
,
.
36.
,
.
37.
,
.
38.
,
.
39.
, 
.
40.
, 
.
2.10. Побудуйте дробово-афінну функцію w за образами трьох точок:
1.
2.
3.
4.
5.
.
6.
.
2.11.
Знайдіть дробово-афінну функцію w,
для якої
:
1.
,
.
2.
,
.
3.
,
.
4.
,
.
2.12.
Доведіть, що кожне дробово-афінне
відображення
,
на
має вигляд
,
де
– довільна точка і
.
2.13. Доведіть, що кожне дробово-афінне відображення на має вигляд
,
де
і
– довільні числа.
2.14. Доведіть, що кожне дробово-афінне відображення на має вигляд
,
де і – довільні числа.
2.15. Покажіть, що дробово-афінне відображення на має вигляд
,
де
a,
b,
c
і d
– довільні дійсні числа такі, що
.
2.16. Нехай . Знайдіть або :
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
,
.
9.
,
.
10.
,
,
.
11.
.
12.
,
.
13.
.
14.
,
.
15.
.
16.
.
17.
.
18.
19.
.
20.
.
2.17.
Нехай
.
Знайдіть
або
:
,
.
,
,
,
.
,
,
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
,
.
,
.
,
.
,
.
,
,
.
,
.
,
., .
,
.
,
., .
,
., .
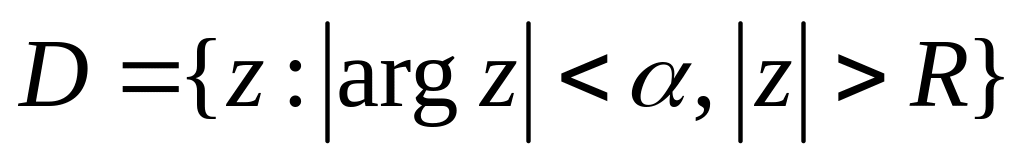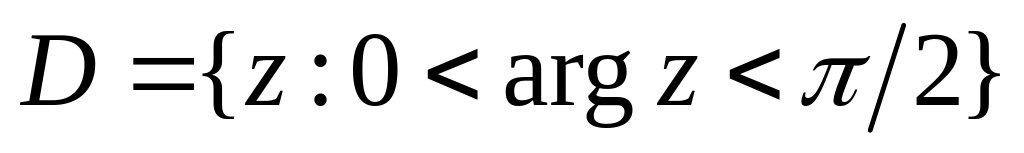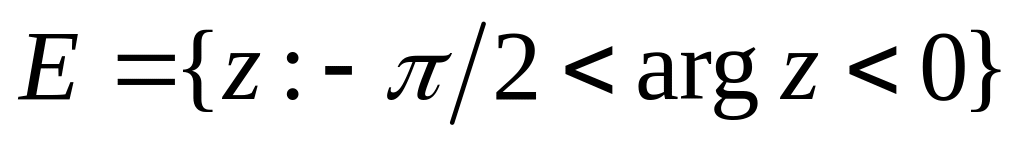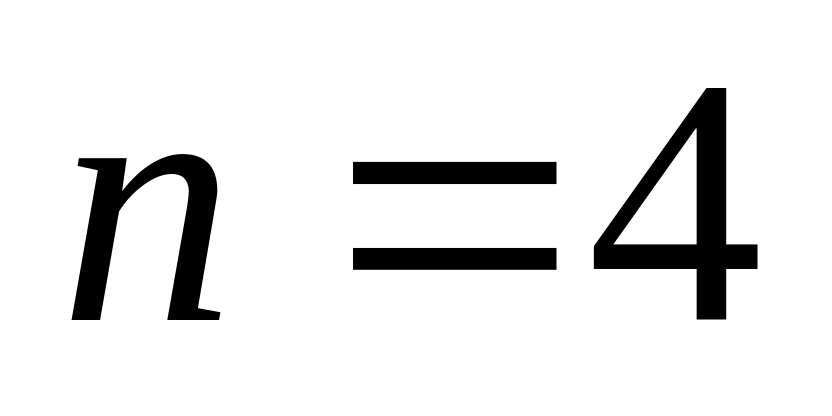2.18.
Нехай
.
Знайдіть
або
:
1.
,
.
2.
.
3.
.
4.
,
.
5.
.
6.
,
.
7. .
8.
.
9. .
10. .
11. .
12.
.
13.
.
14.
.
15.
.
16.
.
17.
.
2.19. Нехай . Знайдіть :
1.
.
2.
.
3.
.
4.
.
5.
,
.
6.
,
.
7.
,
.
8.
.
9.
.
10.
.
11.
,
.
12.
,
.
2.20. Знайдіть конформне і однолисте відображення області на область :
,
.
,
.
,
.
,
.,
.
,
.,
,
., .
,
.
,
.,
.,
.
,
.,
., .
, .
,
.
,
.
,
.
,
.
,
.,
.
,
,
.
,
.
,
.
,
.
,
.,
., .
, .
, .
, .
,
.
,
.
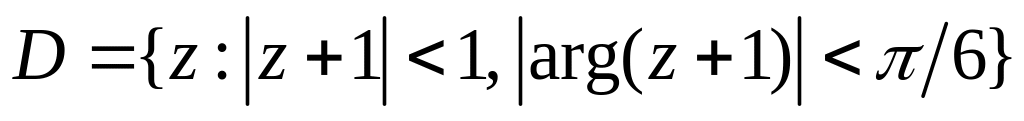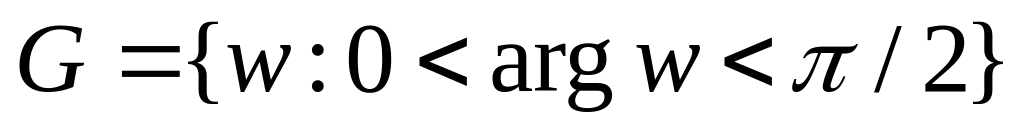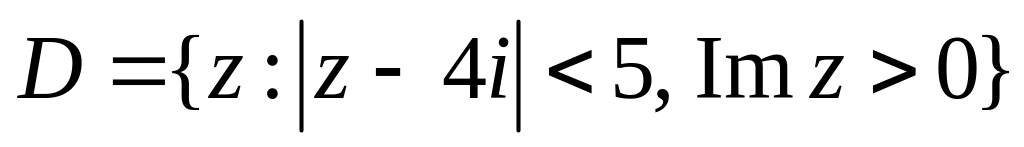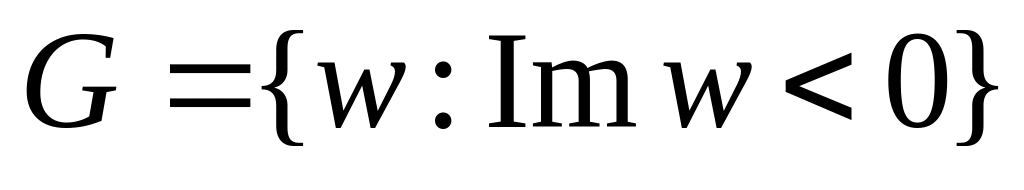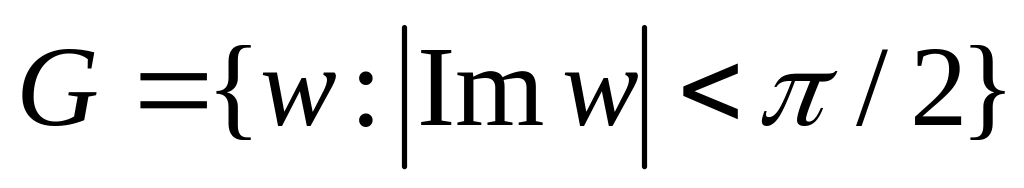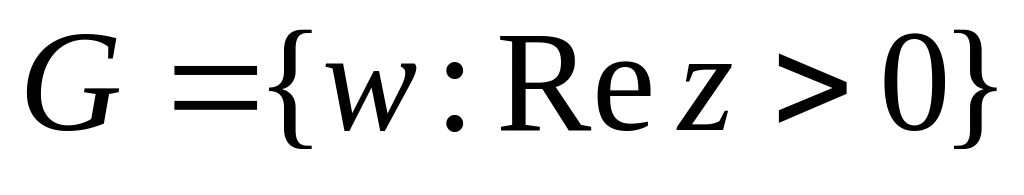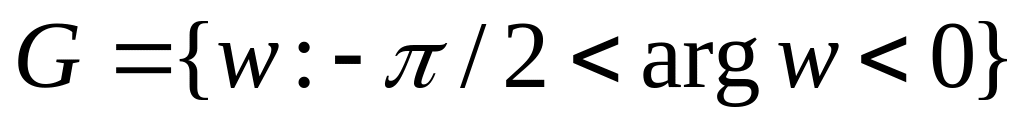2.21. Знайдіть конформне і однолисте відображення області на область :
1.
,
.
2.
,
.
3.
,
.
4.
,
.
5.
,
.
6.
,
.
7.
,
.
8.
,
.
9.
,
.
10.
,
.
11.
,
.