9. Дробово-афінне відображення. Так називається функція

, (1)

де та – сталі, причому

. (2)

Умова (2) рівносильна умові Оскільки , то ця функція є конформним і взаємно однозначним відображенням на . Якщо , то функція (1) є афінною. Нехай . Тоді розглядувану функцію можна подати у вигляді . Бачимо, що дробово-афінне відображення зводиться до послідовного виконання п’яти відображень: а) ; б) ; в) ; г) , де ; д) , тобто .

Приклад 1. Знайдемо прообраз прямої при відображенні

.

Перепишемо останню рівність у вигляді . Тоді

,

звідки

Тому пряма є шуканою. До такого ж результату можна прийти наступними міркуваннями. Відображення переведе розглядувану пряму в пряму , а відображення переводить останню в шукану пряму .

10. Колова властивість дробово-афінного відображення. Пряму будемо називати колом у нескінченного радіуса. Таким чином, коло в є або колом в або прямою в .

Теорема 1. Будь-яка дробово-афінна функція відображає коло в на коло в .

Доведення. Теорему досить довести для функції , оскільки всі інші відображення, композицією яких є дробово-афінне, володіють такою властивістю. Рівняння кола має вигляд . Нехай , . Тоді

, , ,

,

тобто , а це є рівняння кола в w-площині. ►

Теорема 2. Дробово-афінне відображення точки, симетричні відносно кола, відображає на точки, симетричні відносно образа цього кола.

Доведення. Досить розглянути випадок коли . Нехай і – точки, які симетричні відносно кола U (воно може бути і прямою). Оскільки коло , яке проходить через точки і є ортогональними до U і відображення w є конформним, то кола і є ортогональними і проходить через точки і . Отже, точки і є симетричними відносно . ►

Приклад 1. Знайдемо образ кола при відображенні . Для цього перепишемо останню рівність у вигляді . Бачимо, що тоді і тільки тоді, коли , а останнє рівняння задає пряму .

Приклад 2. Знайдемо образ області при відображенні , де . Для цього зауважимо, що , , . Але з рівності отримуємо, що і

.

Бачимо, що тоді і тільки тоді, коли , тобто коли , де , , а . Аналогічно, тоді і тільки тоді, коли , тобто коли . Отож, розглядувана функція відображає кола та відповідно на прямі та . Ці кола ділять площину на чотири області, кожна з яких відображається на одну із областей, на які ділять площину вказані вище прямі. Але . Тому .

11. Побудова дробово-афінного відображення за трьома точками.

Теорема 1. Для будь-яких трьох різних точок , і із і будь-яких різних точок , та із існує єдина дробово-афінна функція

(1)

така, що , , і ця функція має вигляд

, (2)

причому, якщо якась із точок , , , , , збігається з , то відповідні різниці в (2) вважаються рівними 1.

Доведення. Справді, функція (2) є дробово-афінною і , . Далі, якщо деяка дробово-афінна функція має вказану в умові теореми властивість, то записавши рівності , , отримуємо

, ,

, , , .

Поділивши тепер відповідні різниці, переконуємось, що розглядувана функція подається у вигляді (2). Отже, така функція єдина. ►

Наслідок 1. Кожне коло в можна відобразити на будь-яке коло в за допомогою дробово-афінної функції.

Наслідок 2. Будь-який круг у можна конформно і однолисто відобразити на будь-який круг у за допомогою дробово-афінної функції.

Для побудови такого відображення потрібно на колах і взяти відповідно трійки точок , , та , , так, щоб вони задавали однакову орієнтацію цих кіл і скористатися формулою (2).

Приклад 1. Знайдемо дробово-афінну функцію, яка відображає круг на праву півплощину . Для цього візьмемо точки , , та , , і підставимо їх у формулу (2). Отримуємо

, .

Приклад 2. Покажемо, що формула

, , (3)

задає всі дробово-афінні відображення півплощини на круг . Справді, якщо – таке відображення, то деяка точка відображається в точку . Тоді точка , яка є симетричною до точки відносно уявної осі, відображається на точку , яка є симетричною до точки відносно . Робимо висновок, що розглядуване відображення необхідно має вигляд (3). Навпаки, якщо – відображення виду (3), то

, .

Але

і . Тому . Отже, кожне розглядуване відображення має вигляд (3). Навпаки, якщо – відображення вигляду (3), то і . Тому .

12. Відображення , для . Якщо , то . Отже, функція є конформним відображенням в кожній точці і відображає промінь на промінь . Окрім цього, тоді і тільки тоді, коли , де і . Звідси випливає, що областями однолистості функції є такі області, які не містять таких двох різних точок і , що і , . До таких областей належать, зокрема, кути . Кожну область функція конформно і однолисто відображає на область , причому промені і відображаються відповідно на верхній та нижній береги розрізу. Таким чином, звуження функції на область має обернену функцію , яка відображає конформно і однолисто на , причому

, ,

і є однозначною гілкою функції в області . При будь-якому області також є областями однолистої функції . Кожну таку область функція конформно і однолисто відображає на область . Тому в області існує голоморфна гілка функції , яка конформно і однолисто відображає область на .

Рис. 1

Функція є n-значною. Її можна розглядати як однозначну на її рімановій поверхні, модель якої можна уявити так. Візьмемо n накладених одна на одну областей , . Склеїмо нижній берег розрізу з верхнім берегом розрізу , нижній берег розрізу з верхнім берегом розрізу і т.д., нижній берег розрізу з верхнім берегом розрізу . Побудований об’єкт називається моделлю ріманової поверхні функції . Ріманова поверхня функції є n-листою. Над кожною точкою лежить n точок поверхні, які проектуються в . Точка називається алгебраїчною точкою розгалуження порядку функції . Вважаючи, що на належить проміжку , приходимо до висновку, що функція взаємнооднозначно відображає свою ріманову поверхню на .

Теорема 1. При будь-яких і в будь-якому крузі такому, що , існує голоморфна гілка функції , яка в точці приймає значення .

Доведення. Справді, при деякому . ►

Теорема 2. В кожній області такій, що звуження функції на деяку область є однолистим відображенням на , існує голоморфна гілка функції .

Доведення. Справді, функція обернена до вказаного звуження має похідну в кожній точці області .►

Останні дві теореми будуть узагальнені в наступних розділах.

Приклад 1. Функція промінь відображає на промінь . Ця ж функція кут конформно і однолисто відображає на кут . Ця ж функція півплощину , відображає на множину , тобто на множину . При цьому кут відображається на верхню півплощину, кут – на нижню півплощину, кут – на верхню півплощину. Отож, функція не є однолистим відображенням кута на .

Приклад 2. Функція конформно і однолисто відображає кут на півплощину .

Приклад 3. Знайдемо функцію, яка конформно і однолисто відображає кут на круг . Для цього розглянемо функції , та

.

Тоді функція

є шуканою, бо

, , .

Приклад 4. Знайдемо функцію, яка конформно і однолисто відображає півплощину на кут . Для цього розглянемо функції , та , де під розуміється голоморфна гілка кореня в , яка в точці 1 приймає значення 1. Тоді функція є шуканою, бо , , .

Приклад 5. Знайдемо функцію, яка конформно і однолисто відображає півплощину на . Для цього розглянемо функції , та , де під розуміється голоморфна гілка кореня в , яка в точці 1 приймає значення 1. Тоді функція є шуканою, бо

, ,

.

13. Відображення і . Оскільки і , то функція є конформним відображенням в кожній точці . Крім цього, тоді і тільки тоді, коли , . Тому функція є однолистою в будь-якій області , яка не містить двох таких різних точок і , що , _. Зокрема, вона є однолистою в смузі . Записавши і із рівності бачимо, що тоді і тільки тоді, коли . Отож, функція взаємно однозначно і конформно відображає смугу на область , тобто на всю площину без променя . При цьому дійсна пряма переходить у верхній берег розрізу, а пряма – в нижній. Крім цього,

,

.

Аналогічно, кожну смугу функція конформно і однолисто відображає на область . Тому звуження функції на

Рис. 1

кожну область має обернену функцію , яка відображає взаємно на , причому

.

Теорема 1. При будь-яких і в кожному крузі такому, що , існує однозначна голоморфна гілка функції , яка в точці приймає значення .

Доведення. Справді такий круг належить деякій області при деякому . ►

Теорема 2. В кожній області такій, що звуження функції на деяку область є однолистим відображенням на , існує голоморфна гілка функції .

Доведення. Справді, функція обернена до вказаного звуження має похідну в кожній точці області . ►

Останні дві теореми будуть узагальнені в наступних розділах.

Функція є нескінченнозначною. Її можна розглядати як однозначну на її рімановій поверхні, модель якої можна собі уявити так. Візьмемо послідовність областей , де . Склеїмо нижній берег розрізу області з верхнім берегом розрізу області . Так побудований об’єкт називається моделлю ріманової поверхні функції . Ріманова поверхня функції є нескінченнолистою. Над кожною точкою лежить нескінчена кількість точок ріманової поверхні, які проектуються в . Точка називається логарифмічною або трансцендентною точкою розгалуження. Вважаючи, що на належить проміжку приходимо до висновку, функція взаємно однозначно відображає свою ріманову поверхню на .

Рис. 2

Приклад 1. Знайдемо функцію, яка конформно і однолисто відображає смугу на півплощину . Для цього розглянемо функції , , де – гілка кореня в , яка в точці 1 приймає значення 1. Тоді функція є шуканою, бо , .

Приклад 2. Знайдемо функцію, яка конформно і однолисто відображає півплощину на смугу . Для цього розглянемо функції , , , де – гілка логарифма в , яка в точці 1 приймає значення 0. Тоді функція є шуканою, бо , , .

Приклад 3. Функція конформно і однолисто відображає кут , , на півплощину .

Приклад 4. Знайдемо функцію, яка конформно і однолисто відображає на . Розглянемо функції , , де – голоморфна гілка в відповідної багатозначної функції, яка в точці 1 приймає значення 1. Тоді функція є шуканою, бо

,

,

.

Приклад 5. Знайдемо функцію, яка конформно і однолисто відображає на . Для цього розглянемо функції , , та , де – голоморфна гілка в відповідної багатозначної функції, яка в точці 1 приймає значення 1. Тоді функція

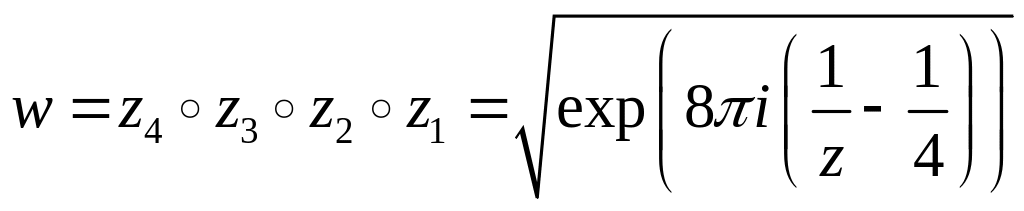
є шуканою, бо

,

,

, .

Приклад 6. Знайдемо функцію, яка конформно і однолисто відображає смугу на . Для цього розглянемо функції та . Тоді функція є шуканою, бо , .