Розділ 2

Розділ 2. Голоморфні функції і конформні відображення

1. Похідна функції . Похідною функції в точці називається границя

,

тобто

.

Правила знаходження похідної функції такі ж, як і функції , і доводяться аналогічно.

1. Похідна сталої дорівнює нулеві: .

2. (однорідність) для кожної сталої , якщо існує.

3. (адитивність) Похідна суми дорівнює сумі похідних, якщо останні існують: .

4. (лінійність) для будь-яких сталих і , якщо похідні і існують.

5. , якщо похідні і існують.

6. , якщо похідні і існують та .

7. Якщо функція g має похідну в точці , а функція f – в точці , то функція має похідну в точці і , тобто .

8. Якщо функція є однолистим відображенням області D на область G і має похідну в точці , то обернена функція має похідну в точці і

.

Безпосередньо з означення похідної випливає також, що , і т.д.

2. Умови Коші-Рімана. Знайдемо умови на функції і , за яких функція має похідну в заданій точці.

Теорема 1. Для того щоб функція мала похідну в точці , необхідно і достатньо, щоб функції і , як функції двох змінних, були диференційовними в точці і в цій точці виконувались умови Коші-Рімана:

(1)

Якщо умови (1) виконуються, то

. (2)

Доведення. Нехай функція має похідну в точці . Тоді існує

.

Отже, , де , коли . Нехай , і . Тоді

,

.

Тому функції u і v є -диференційовними функціями і

, , , .

Отже, (1) виконується. Нехай тепер функції і є -диференційовними і виконуються умови (1). Тоді

,

де , якщо , бо , і , , та , якщо . Звідси випливає, що функція має похідну в точці і справедлива формула (1). ►

Приклад 1. Нехай . Тод , ,

, , ,

Отже, умови (1) виконуються в кожній точці і

.

Приклад 2. Нехай . Тоді , ,

, , , .

Отже, умови (1) виконуються в кожній точці і .

Приклад 3. Нехай

Тоді , , для кожного . Тому (тут похідні розуміються як похідні функції в ) для кожного . Водночас, , якщо . Тому похідної в розумінні комплексного аналізу ця функція в точці не має.

Приклад 4. Нехай . Тоді , ,

, , , .

Обидві умови (1) не виконуються в жодній точці. Отже, розглядувана функція не має похідної в кожній точці .

Зауваження 1. Останній приклад показує, що умови (1) не задовольняють досить прості -диференційовані функції. Функція називається -диференційовною, якщо функції та є -диференційовними. При цьому називається -диференціалом функції f . Згадавши, що

,

і позначивши , ,

, ,

маємо . Функція f називається -диференційовною, якщо вона є -диференційовною і . Остання умова рівносильна умові (1). Кожна функція , яка є -диференційовною є і -диференційовною, але не навпаки (див. приклад 3). Для -диференційовних функцій і тільки для них , і .

3. Голоморфні функції. Однозначна функція називається голоморфною в точці , якщо вона має похідну в деякому -околі цієї точки. З теореми 1 попереднього пункту випливає, що функція є голоморфною в точці тоді і тільки тоді, коли функції та є -диференційовними функціями в деякому -околі точки і в цьому околі виконуються умови Коші-Рімана. Функція називається голоморфною в області , якщо вона є голоморфною в кожній точці області . Функція називається цілою, якщо вона є голоморфною в , тобто якщо вона має похідну в кожній точці . Функція називається голоморфною на множині Е, якщо вона є голоморфною в кожній її точці. Отже, функція є голоморфною на замкненій області , якщо вона є голоморфною в деякій області такій, що . Функція називається голоморфною в , якщо функція є голоморфною в точці . Множину всіх функцій, голоморфних в області , позначають через .

Теорема 1. Якщо функція є голоморфною і однолистою в області , відображає область на область і для всіх , то обернена функція є голоморфною в .

Доведення. Справді, функція має похідну в кожній точці області . ►

Зауваження 1. Далі покажемо, що деякі умови теореми 1 є зайвими.

Приклад 1. Функції , , , є цілими, бо ,

.

, .

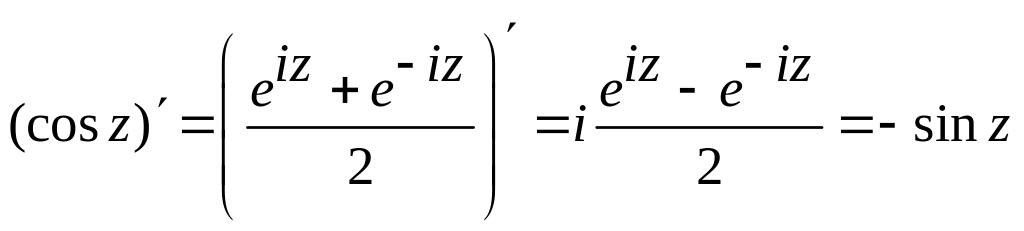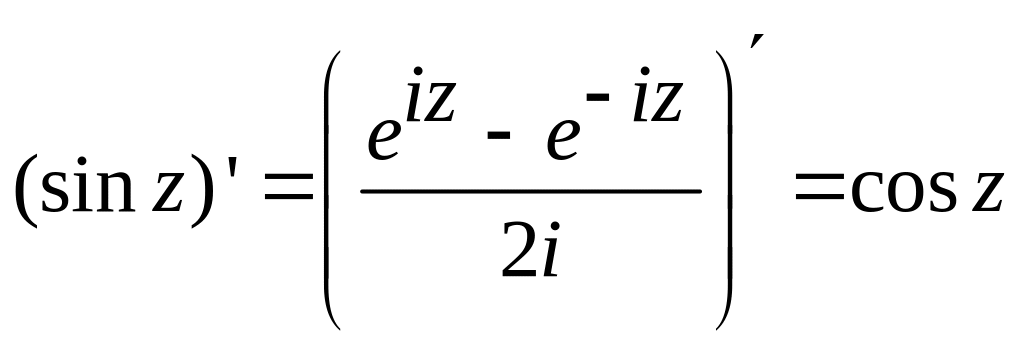Поліном також є цілою функцією. Раціональна функція , де i – нескоротні поліноми, є голоморфною в усіх точках за винятком тих точок , для яких . Функції та не є голоморфними і, тим більше, цілими, оскільки не є однозначними.

Приклад 2. Нехай . Тоді і . Тому

, , , .

Бачимо, що умови Коші-Рімана виконуються тільки в точці і розглядувана функція має похідну тільки в цій точці, причому .

Функція називається моногенною в точці , якщо вона має похідну в цій точці. Останній приклад показує, що моногенна функція в точці не обов’язково є голоморфною в ній.

Зауваження 2. Інколи голоморфні функції називають аналітичними. Ми ж будемо використовувати останній термін для ширшого класу функцій.

4. Геометричний зміст модуля і аргументу похідної. Нехай функція f має похідну в точці i , a –неперервний шлях такий, що в деякій точці існує і . Отже, шлях , проходить через точку . Образом цього шляху буде шлях , який проходить через точку . Оскільки , то  має в точці дотичну, причому кожне є одним із кутів, який утворює дотична з вектором 1=(1;0), тобто з додатним напрямом дійсної осі. Далі, . Тому шлях  в точці має дотичну і кожне є одним із кутів, який утворює ця дотична із додатним напрямом осі . Оскільки аргумент добутку дорівнює сумі аргументів, то

, (1)

і

, , (2)

де . Остання рівність виражає геометричний зміст аргументу похідної: якщо функція f є голоморфною в точці і , то дорівнює куту повороту дотичної до кривої при відображенні . Далі, взявши шлях , який проходить через точку і має в точці дотичну, яка утворює з вектором 1=(1;0) кут , ми в w-площині аналогічно отримаємо шлях , дотична до якого в точці з віссю утворює кут . При цьому і , де . Отже,

. (3)

Рис. 1 Рис. 2

Отже, якщо функція є голоморфною в точці і , то функція зберігає кути між кривими в точці як за величиною, так і за напрямом вимірювання. Ця властивість, виражена рівністю (3), називається консерватизмом кутів.

Границя

(4)

називається коефіцієнтом лінійного розтягу функції в точці . Якщо границя (4) існує і , то функція називається відображенням зі сталим коефіцієнтом лінійного розтягу в точці . Отже, якщо функція має похідну в точці і , то функція є відображенням із сталим коефіцієнтом лінійного розтягу в точці , причому . В цьому полягає геометричний зміст модуля похідної голоморфної функції. Назва «коефіцієнт лінійного розтягу» пов’язана з тим, що для близьких до .

Приклад 1. Знайдемо точки, в яких коефіцієнт лінійного розтягу відображення дорівнює 3. Маємо і тому тільки у випадку, коли , тобто на колі коефіцієнт лінійного розтягу дорівнює 3.

Приклад 2. Знайдемо точки, в яких кут повороту дотичної при відображенні дорівнює . Оскільки , то шуканими є точки променя .

5. Конформні відображення. Функція називається конформним відображенням в точці , якщо існує і . Функція називається конформним відображенням в області , якщо є конформним відображенням в кожній точці .

Теорема 1. Якщо є конформним відображенням в точці , то є однолистою в деякому околі цієї точки.

Доведення. Справді, в протилежному випадку існує послідовність , , , така, що . Тому . Суперечність. ►

Приклад 1. Функція , для якої і для всіх , показує, що якщо є конформним відображенням в кожній точці , то не обов’язково є однолистою в D.

Якщо f є конформним відображенням в області D, то в кожній точці воно має сталий коефіцієнт лінійного розтягу і властивість консерватизму кутів. Можна показати, що і навпаки: кожна функція , яка має ці дві властивості є голоморфною в D функцією і для всіх , тобто f є конформним відображенням в D.

Отож, можна дати інше (рівносильне) означення конформного відображення в точці : відображення околу точки на окіл точки , яке володіє властивістю консерватизму кутів і має сталий коефіцієнт лінійного розтягу в точці а, називається конформним в точці а.

Основними задачами теорії конформних відображень є такі: 1) знайти образ або прообраз заданої множини при заданому конформному відображені; 2) знайти функцію , яка є конформним і однолистим відображенням заданої області на задану область . Основними в цьому напрямку є наступні три теореми, які ми тут доводити не будемо.

Теорема 2 (Рімана). Які б не були дві однозв’язні області і , межа кожної з яких складається більше, ніж з однієї точки, і числа , та , існує єдина функція , яка є конформним і однолистим відображенням на і задовольняє умови , .

Теорема 3 (Каратеодорі). Нехай межі областей і є замкненими жордановими кривими, функція , існування якої стверджується в теоремі Рімана, є взаємно однозначним і неперервним відображенням на . Крім цього, якщо точки , і з та , і з задають додатні орієнтації та відповідно, то існує єдине конформне в і неперервне та взаємно однозначне відображення замкненої області на , для якого , .

Теорема 4. Якщо дві обмежені області і мають жорданові межі і голоморфна в та неперервна в функція f є взаємно однозначним відображенням на зі збереженням орієнтації, то є взаємно однозначним відображенням на .

Нехай , , – додатна параметризація . Кажуть, що відображення зберігає орієнтацію, якщо шлях , , також є додатною параметризацією , тобто, якщо точка рухається до точки через точку по , то точка , рухаючись по до точки , проходить через точку . Кажуть, що точки і із задають додатну орієнтацію , якщо для деякої її додатної параметризації , , існують такі точки і , , що , .

Функція називається конформним відображенням в точці , якщо функція або є конформним відображенням в цій точці як функція із в . Функція називається конформним відображенням в , якщо функція є конформним відображенням із в у точці 0.

Приклад 2. Функція є конформним відображенням в кожній точці як функція із в і є конформним відображенням в кожній точці як функція із в .

Приклад 3. З’ясуємо, в яких точках функція є конформним відображенням. Маємо і, отже, розглядувана функція є конформним відображенням у кожній точці множини .

Зауваження 1. Інколи розглядають антиконформні відображення або конформні відображення другого роду. Це відображення, які мають вигляд , де F – конформне відображення. Можна також сказати, що антиконформні відображення – це такі функції, для яких , а . Антиконформні відображення мають сталий коефіцієнт лінійного розтягу і зберігають кути між кривими, але тільки за величиною: . Важливу роль відіграють і квазіконформні відображення. Не вдаючись в деталі відзначимо, що це такі функції , для яких є в певному розумінні малим у порівнянні з . Відображення називається регулярним в точці , якщо воно є однолистим в деякому околі точки і в цьому околі існують неперервні частинні похідні і , причому

.

Якщо є конформним відображенням в точці , то з умов Коші-Рімана отримуємо

.

Далі ми побачимо, що голоморфна функція має похідні всіх порядків. Тому кожне конформне відображення в деякому околі точки є регулярним відображенням у точці . Якщо функція є -диференційована в точці , то функції і мають у точці дотичні площини, рівняння яких

, ,

, .

Ці два рівняння можна записати одним рівнянням у комплексній формі , . Останнє відображення називається дотичним відображенням. Якщо функція голоморфна в точці , то і дотичне відображення має вигляд , .

6. Лінійне відображення. Так називається функція , де – стала. Оскільки , то ця функція є конформним і взаємно однозначним відображенням на , а також на . З рівності видно, що за такого відображення точку отримують з точки шляхом повороту на кут навколо точки і гомотетії з центром в початку координат і коефіцієнтом . Отож, лінійна функція є композицією двох відображень: повороту і гомотетії .

Приклад 1. Функція є конформним і однолистим відображенням на .

Приклад 2. Функція є конформним і однолистим відображенням на .

Приклад 3. Функція є конформним і однолистим відображенням на .

7. Афінне відображення. Так називається функція , де та b сталі. Оскільки , то ця функція є конформним і взаємно однозначним відображенням на , а також на . За такого відображення точку отримують з точки шляхом повороту навколо початку координат на кут , гомотетії з центром в початку координат і з коефіцієнтом та паралельного перенесення на вектор b. Отож, афінна функція є композицією трьох відображень: 1) повороту , 2) гомотетії , 3) паралельного перенесення .

Приклад 1. Функція є конформним і однолистим відображенням півплощини на півплощину .

Приклад 2. Знайдемо образ круга при відображенні . Оскільки , де , , , , і , то . До того ж результату можна прийти записавши рівність у вигляді . Тоді і бачимо, що тоді і тільки тоді, коли .

Зауваження 1. У випадку функцію можна подати у вигляді і розглядати як композицію двох відображень: паралельного перенесення і повороту навколо точки .

8. Симетричні точки. Точки і називаються симетричними відносно прямої , якщо вони лежать на одному перпендикулярі до , на однаковій відстані від і належать різним півплощинам, на які ділить . Точки і є симетричними відносно прямої тоді і тільки тоді, коли . Функція є, таким чином, симетрією відносно дійсної осі. Точки і називаються симетричними відносно кола , якщо вони лежать на одному промені, який виходить з точки , і добуток їх відстаней до точки дорівнює . Точки і вважаються симетричними відносно .

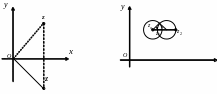
Рис. 1 Рис. 2

Теорема 1. Для того щоб точки і були симетричними відносно кола , необхідно і достатньо щоб виконувалась принаймні одна з наступних умов: 1) ; 2) кожне коло, яке проходить через точки і було ортогональним до кола .

Доведення. Обмежимось розглядом першої умови. Нехай точки і симетричні. Тоді і

.

Навпаки, якщо 1) виконується, то і , тобто точки і симетричні. ►

Відображення, яке точці ставить у відповідність точку , симетричну відносно кола, називається симетрією відносно кола або інверсією.

Наслідок 1. Точки і є симетричними відносно кола тоді і тільки тоді, коли , тобто функція є інверсією відносно кола . Функція є композицією інверсії відносно кола і симетрії відносно дійсної осі.

Приклад 1. Знайдемо точку симетричну точці відносно кола . Маємо , . Тому точка є шуканою.