Лишки…

Розділ 5. Лишки та їх застосування до знаходження інтегралів

1. Означення і обчислення лишків. Лишком або залишком в точці функції , голоморфної в деякому проколеному околі точки a, називається інтеграл

(1)

де є таким, що функція, що є голоморфною в для для деякого .

Теорема 1. Лишок в точці функції , голоморфної в деякому проколеному околі точки , знаходиться за формулою

(2)

де – відповідний (тобто з номером “-1”) коефіцієнт лоранового розвинення функції в околі точки .

Доведення. Ця теорема випливає безпосередньо із означень. ►

Теорема 2. Якщо в точці функція має простий полюс, то

.

Доведення. Справді,

.►

Наслідок 1. Нехай , функції і є голоморфними в точці , і має в точці простий нуль. Тоді .

Доведення. Справді, оскільки , то

.►

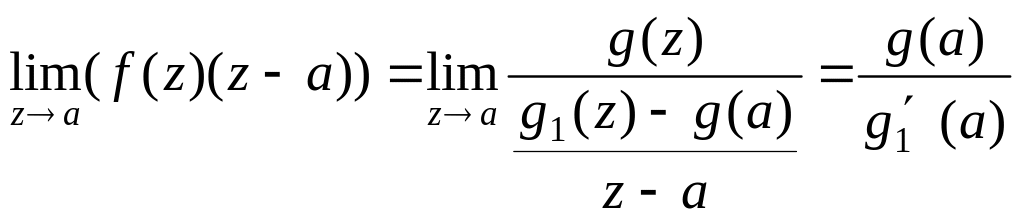Терема 3. Якщо в точці функція має полюс порядку , то

.

Доведення. Справді, це випливає з рівності

.►

Зауважимо, що якщо є усувною особливою точкою, то . Це випливає з теореми Коші. Приклад показує, що для сказане вище не є справедливим. Отож, лишки природно рахувати в скінчених неусувних ізольованих особливих точках, а також в , якщо функція є голоморфною в деякому проколеному околі .

Приклад 1. Функція в точці має полюс другого порядку . Тому

.

Приклад 2. Якщо , то

, .

Приклад 3. Якщо , то

,

,

, .

Приклад 4. Знайдемо лишки в усіх ізольованих особливих точках функції 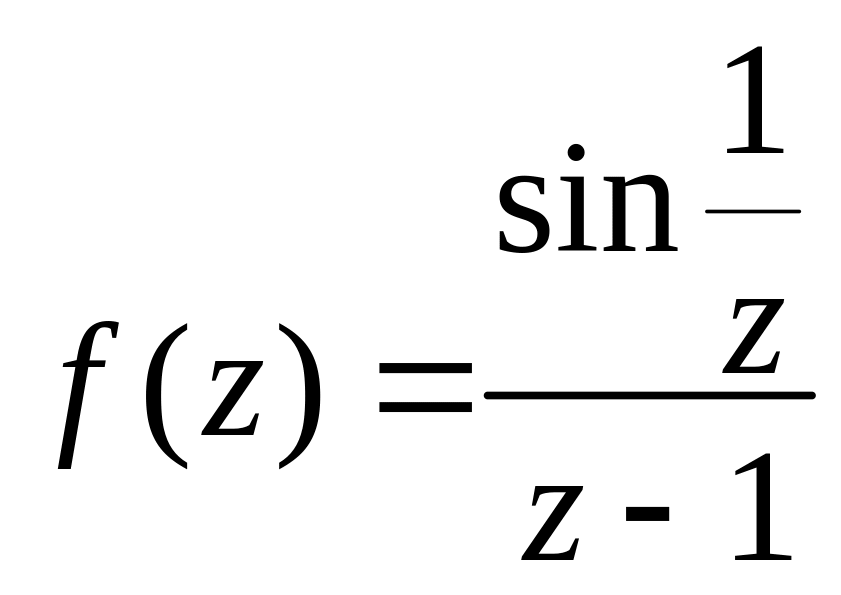. Особливими точками є а₁ = 1 – простий полюс, а₂ = 0 – істотно особлива точка, a₃= – усувна особлива точка.

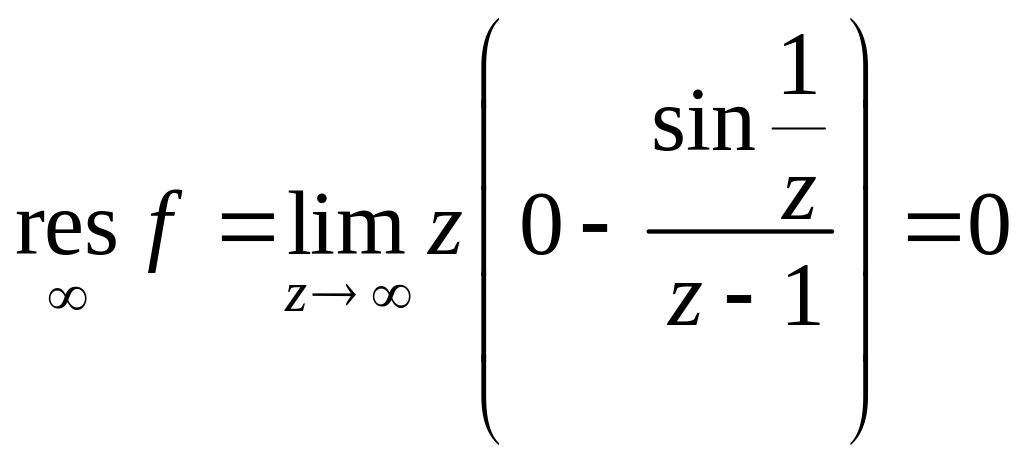, , бо 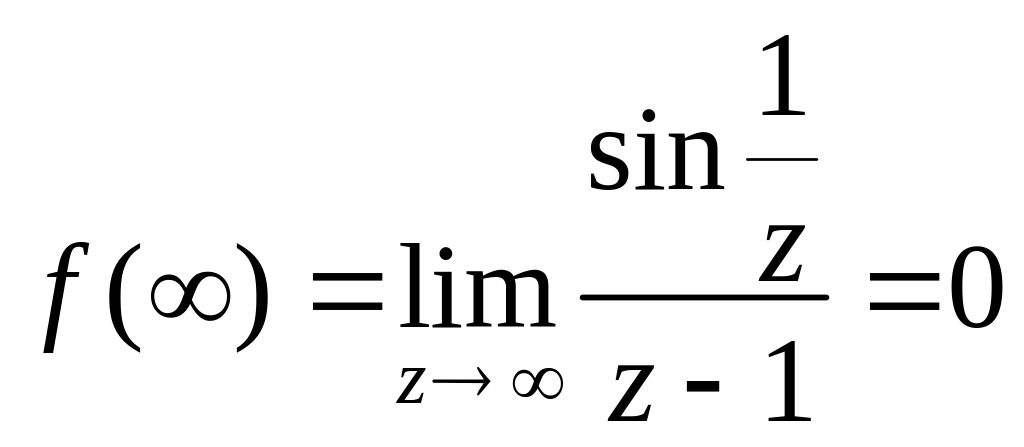. Лишок в точці 0 знайдемо за формулою (2). Оскільки , а , то .

2. Основна теорема про лишки.

Теорема 1. Нехай межа обмеженої області складається зі скінченого числа замкнених жорданових спрямлюваних кривих, , – деякі точки області , а функція є голоморфною в і неперервною в . Тоді

.

Доведення. Нехай , де числа є настільки малими, що . Тоді за узагальненою теоремою Коші застосованою до області отримуємо

,

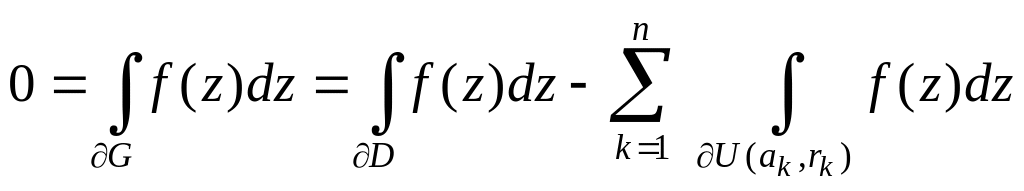
звідки випливає потрібне. ►

Теорема 2. Нехай існує точок таких, що функція є голоморфною в області . Тоді сума всіх залишків функції дорівнює нулеві, тобто

.

Доведення. Нехай є таким, що для всіх , а

де є настільки малими, що круги не перетинаються і лежать в . Тоді згідно з теоремою Коші

,

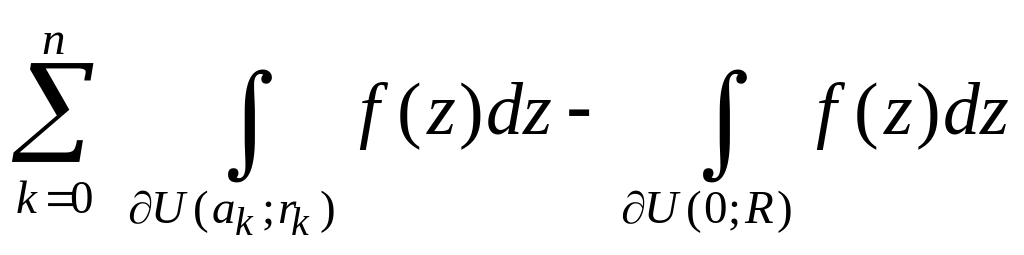
звідки випливає потрібне. ►

Приклад 1. Для знаходження інтегралу

зауважимо, що скінчені особливі точки підінтегральної функції лежать в крузі . Тому згідно з теоремами 1 та 2

.

Але і лишок підінтегральної функції в дорівнює 0. Отож,

.

Приклад 2. Для знаходження інтегралу

зауважимо, що і підінтегральна функція в крузі має дві особливі точки та , які є простими полюсами. Тому

.

3. Знаходження інтегралів деяких тригонометричних функцій. Розглянемо інтеграл

, , ,

де – раціональна функція двох змінних. Нехай . Тоді

, ,

.

Тому

,

де – раціональна функція. Якщо на функція не має особливих точок, то за основною теоремою про лишки

,

де – особливі точки .