7.2.2 Гідравлічна ув’язка кільцевої мережі

Після призначення діаметрів ділянок мережі розрахунок із техніко-економічної стає чисто гідравлічною задачею і полягає у знаходженні дійсних потокорозподілів для вже відомих діаметрів ділянок мережі. При цьому використовується 2-ий закон Кірхгофа (алгебраїчна сума втрат напору в кільцях дорівнює нулю). Докладно методи гідравлічної ув’язки кільцевої мережі розглянуті в лекції № 9.

7.3 Принцип гідравлічної ув’язки кільцевої водопровідної мережі

Як зазначалось, гідравлічна ув’язка – це знаходження дійсного (істинного) потокорозподілу при відомих діаметрах труб ділянок мережі та вузлових витратах води. Цю задачу можна розв’язати за допомогою двох законів Кірхгофа. Перший закон Кірхгофа виконується автоматично у процесі потокорозподілу; при цьому для кожного вузла розв’язується рівняння типу ΣQ=0. Таких рівнянь буде m-1, де m – кількість вузлів. Це

вузла

пояснюється тим, що у кільцевій мережі з одним джерелом живлення в останньому вузлі буде тотожність, тобто при попередньому розподілі води в мережі розв’язується (m -1) рівнянь типу ΣQ=0.

вузла

Отже, далі гідравлічна ув’язка кільцевої мережі з одним джерелом живлення зводиться до розв’язування n рівнянь типу Σh=0, тобто рівнянь

кільця

2-го закону Кірхгофа. Зробимо математичний опис цих рівнянь, пам’ятаючи, що втрати напору можна обчислити за простою формулою h=sq^β:

S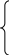 ₁₁q₁₁^β+ S₁₂q₁₂^β+…+ S_1pq_1p^β=0;

……………………………….

………………………………. (7.4)

……………………………….

S_n1q_n1^β+S_n2q_n2^β+…+S_npq_np^β=0,

де S – опір ділянки; β – показник степеня, який залежить від режиму руху води в трубах; для ламінарного режиму β=1 і для турбулентного режиму β=1,75...2; p, n – кількість відповідно ділянок та кілець мережі.

Перший індекс при опорі й витраті води відповідає номеру кільця, а другий – номеру ділянки у кільці. Слід мати на увазі, що у водопровідних трубах ламінарний рух води відсутній. Тому розрахунки виконують або для зони квадратичного опору турбулентного режиму, в котрій β=2, або для перехідної зони турбулентного режиму (пластмасові, скляні, залізобетонні труби), в якій β≈1,75...1,85.

Як бачимо, гідравлічна ув’язка зводиться до розв’язування системи n нелінійних рівнянь. Якщо кілець мережі багато (наприклад, більше від десяти), то таку систему нелінійних рівнянь важко розв’язати навіть із допомогою сучасних ЕОМ (потрібно багато машинного часу). Тому фахівці у галузі водопостачання розробили ітеративні методи, які дають змогу робити гідравлічну ув’язку мережі методами послідовного наближення (ітерації).

Так, якщо використати метод Ньютона для розв’язування системи нелінійних рівнянь відносно витрати води, то можна від цієї системи нелінійних рівнянь перейти до системи лінійних рівнянь відносно поправкової витрати води Δq. Інакше кажучи, до відомої, але неправильної витрати води q шукаємо невідому поправкову витрату води Δq і знаходимо правильне значення витрати води q. Розкриваємо біном Ньютона:

(q+Δq)^β=q^β+βq^β-1Δq+β(β-1)q^β-2Δq²/2!+…+Δq^β. (7.5)

Залишимо тільки два перших доданки з лінійною залежністю від Δq. Унаслідок цього перетворення втрачається точність розв’язування, але система нелінійних рівнянь відносно q перетворюється у систему лінійних рівнянь відносно Δq. Цю систему рівнянь можна розв’язувати (наприклад, із допомогою ЕОМ) і знаходити поправкові витрати Δq. Але коли кілець у мережі багато, то й ця задача потребує багато часу. Були розроблені методи, за допомогою яких цю задачу розв’язати простіше, наприклад методом послідовного наближення. Такий метод запропонував у 1934 р. професор Московського інженерно-будівельного інституту В.Г.Лобачов [4].