4.7. Метод наименьших квадратов для обработки результатов экспериментов.

Данный метод относится к классу аппроксимационных методов. Идея метода состоит в том, чтобы по данным эксперимента построить приближенно функцию, отображающую зависимость ее от , в виде многочлена с тем расчетом, чтобы сумма квадратов отклонений построенной функции от экспериментальной в узловых точках была минимальна. Будем строить функцию в виде многочлена

.

Используем для построения результаты эксперимента, заключенные в таблице

			…
			…

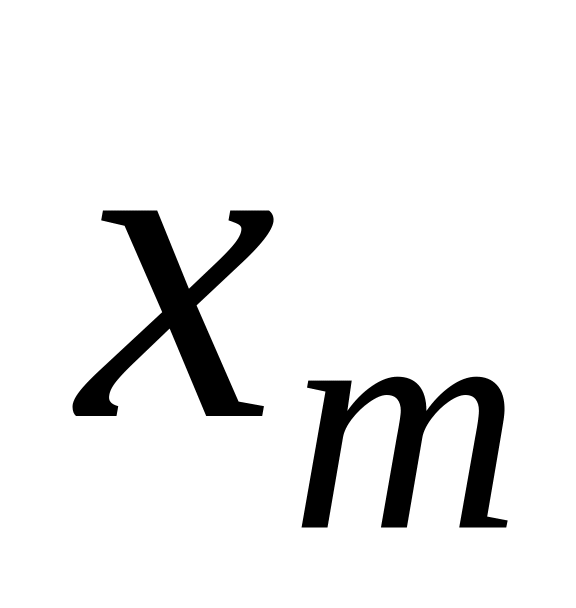
Построить многочлен, значит, определить его коэффициенты . Для этого введем функцию и потребуем, чтобы , где - отклонение функции от экспериментальной в узлах .

Используя вид , получим:

.

Необходимыми условиями экстремума функции является равенство нулю ее первой производной по всем переменным . Расписав эти условия, получим СЛАУ вида:

Запишем систему для определения в нормальной форме:

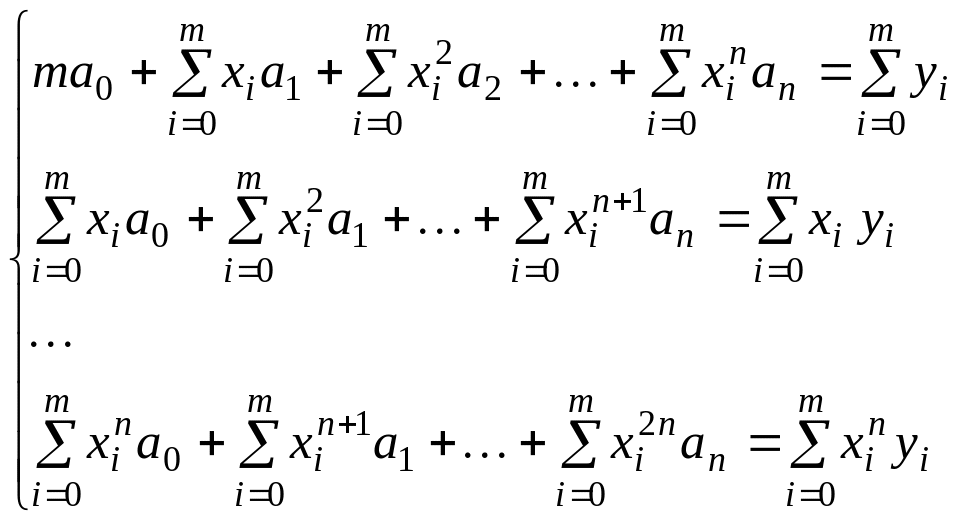
Решаем систему одним из известных методов и находим , которые затем подставляем в искомый многочлен.

Запишем алгоритм метода наименьших квадратов.

1. Вводим таблицу чисел .

2. Вычисляем .

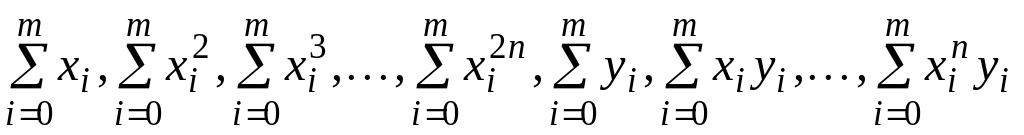3. Решая любым известным методом полученную систему линейных алгебраических уравнений, находим - коэффициенты искомого многочлена.

Для таблицы узловых точек, приведенных выше, построим аппроксимационный многочлен второго порядка методом наименьших квадратов вида:

.

Для этого необходимо вычислить следующие суммы

и решить СЛАУ относительно неизвестных коэффициентов вида:

Значения неизвестных коэффициентов равны:

.

Тогда искомый многочлен второго порядка будет иметь вид:

.

Нетрудно заметить, что в узловых точках значения многочлена и табличной функции не совпадают. Погрешность вычислений по данной формуле в контрольной точке, по сравнению с истинным значением, составляет

.

6. Решение обыкновенных дифференциальных уравнений и систем.

Дифференциальные уравнения являются основным математическим инструментом моделирования и анализа разнообразных явлений и процессов в науке и технике.

Методы их решения подразделяются на два класса:

1. аналитические методы, в которых решение получается в виде аналитических функций;

2. численные (приближенные) методы, где искомые интегральные кривые получают в виде таблиц их численных значений.

Применение аналитических методов позволяет исследовать полученные решения методами математического анализа и сделать соответствующие выводы о свойствах моделируемого явления или процесса. К сожалению, с помощью таких методов можно решать достаточно ограниченный круг реальных задач. Численные методы позволяют получить с определенной точностью приближенное решение практически любой задачи.

Решить дифференциальное уравнение

(16)

численным методом означает, что для заданной последовательности аргументов и числа , не определяя аналитического вида функции , найти значения , удовлетворяющие условиям:

_.

Рассмотрим три наиболее распространенных при решении практических задач численных метода интегрирования Эйлера, Рунге-Кутта и Адамса.