
01_03 Лекции ФМП
.pdf
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Множества евклидова пространства
Определение. Назовем m – мерным координатным пространством множество всевозмож- |
||||||||||||||||
ных упорядоченных совокупностей x1 , x2 , , xm |
вещественных чисел x1 , |
x2 ,…, xm . |
|
|||||||||||||
Для обозначения m –мерного координатного пространства используется символ Rm . |
|
|||||||||||||||
Определение. Упорядоченная совокупность |
x1 , |
x2 , , xm называется точкой m – мерного |
||||||||||||||
координатного пространства, а числа x1 , |
x2 ,…, xm |
|
называются координатами данной точки. |
|
||||||||||||
Обозначим точку |
m –мерного координатного |
пространства |
буквой |
M , тогда запись |
||||||||||||
M (x1 , x2 , , xm ) означает, что точка M имеет координаты x1 , x2 ,…, xm . |
|
|
|
|
||||||||||||
Определение. |
Координатное пространство |
Rm |
называется |
|
m –мерным евклидовым про- |
|||||||||||
странством, |
если между любыми точками M (x |
, x , , x |
) и M (x , x , , x ) |
пространства |
Rm |
|||||||||||
|
|
|
|
|
1 |
|
2 |
m |
|
|
1 |
2 |
|
m |
|
|
определено расстояние, обозначаемое символом M , M |
и равное |
|
|
|
|
|
|
|||||||||
|
|
M , M |
|
|
|
|
. |
|
|
|
||||||
|
|
x |
x 2 x |
x 2 x |
x 2 |
|
|
|
||||||||
|
|
|
|
1 |
1 |
2 |
2 |
|
m |
|
|
m |
|
|
|
|
Будем обозначать m –мерное евклидово пространство так же символом Rm . |
|
|
||||||||||||||
Рассмотрим различные множества точек m –мерного евклидова пространства Rm . |
|
|||||||||||||||
Пусть |
{M} |
– |
некоторое |
множество |
|
точек |
M (x , x |
2 |
, , x |
m |
) пространства |
Rm , |
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
M 0 (x10 , x20 , , xm0 ) Rm и R – некоторое положительное число.
1.Множество {M} точек M , удовлетворяющих условию (M , M 0 ) R , называется m – мерным шаром радиуса R с центром в точке M 0 .
2.Множество {M} точек M , удовлетворяющих условию (M , M 0 ) R , называется открытым m –мерным шаром радиуса R с центром в точке M 0 .
3.Множество {M} точек M , удовлетворяющих условию (M , M 0 ) R , называется m – мерной сферой радиуса R с центром в точке M 0 .
Отметим, что при m 2 множества 1, 2 и 3 представляют собой соответственно круг, открытый круг и окружность радиуса R с центром в точке M 0 .
4.Открытый m –мерный шар радиуса 0 с центром в точке M 0 называется –
окрестностью точки M 0 .
5.Множество {M} точек M , координаты x1 , x2 , , xm которых удовлетворяют неравенст-
вам
x x0 |
d , |
x |
2 |
x0 |
d |
2 |
,…, |
x |
m |
x0 |
d |
m |
, |
1 1 |
1 |
|
2 |
|
|
|
m |
|
|
где d1 , d2 ,..., dm – некоторые положительные числа, называется открытым m – мерным паралле-
лепипедом с центром в точке M 0 или прямоугольной окрестностью точки M 0 . При m 2 это множество представляет собой открытый прямоугольник.
6.Точка M множества {M} называется внутренней точкой этого множества, если существует – окрестность точки M , все точки которой принадлежат множеству {M} .
7.Точка M 0 называется граничной точкой множества {M} , если в любой – окрестности
точки M 0 найдутся точки, как принадлежащие множеству {M} , так и не принадлежащие ему.
Отметим, что граничная точка множества может, как принадлежать этому множеству, так и не принадлежать ему.
8.Множество {M} называется открытым, если все его точки – внутренние.
9.Множество {M} называется замкнутым, если оно содержит все свои граничные точки.
1

10. Точка M 0 называется предельной точкой множества {M} , если в любой – окрестности точки M 0 содержатся точки множества {M} , отличные от M 0 . Предельная точка множества
может принадлежать, а может не принадлежать этому множеству.
Также можно заметить, что множество {M} замкнуто тогда и только тогда, когда оно содержит все свои предельные точки.
11.Множество {M} называется ограниченным, если найдется m – мерный шар, содержащий все точки этого множества.
12.Непрерывной (или простой) кривой L в пространстве Rm называется множество {M}
точек этого пространства, координаты x1 , x2 , , xm которых представляют собой непрерывные функции параметра t :
x1 1 (t) , x2 2 (t) ,…, xm m (t) , t .
Если функции i (t) , i 1, m непрерывно дифференцируемы на отрезке [ , ], то кривую L назы-
вают гладкой.
13.Множество {M} называется связным, если любые две точки этого множества можно соединить непрерывной кривой, все точки которой принадлежат этому множеству.
14.Областью называется открытое и связное множество в пространстве Rm .
15.Если множество {M} представляет собой область, то множество {M } , полученное присоединением к множеству {M} всех его граничных точек, называется замкнутой областью.
Понятие функции многих переменных
Пусть {M} – множество точек пространства Rm .
Определение. Если каждой точке M (x1 , x2 , , xm ) из множества {M} поставлено в соответствие по закону f некоторое число u , то говорят, что на множестве {M} задана функция m пе-
ременных u f (M ) . Для |
функции |
m переменных используются также обозначения |
u f (x1 , x2 , , xm ) или u u(M ) . |
|
|
Числовые переменные |
x1 , x2 , , xm |
называются независимыми переменными или аргумен- |
тами функции. Множество {M} называется областью определения (или областью задания) функ-
ции u f (M ) . Число u , соответствующее данной точке M из множества {M} , называется значением функции в точке M . Совокупность {u} всех значений функции u f (M ) называется мно-
жеством значений этой функции.
В евклидовом пространстве R2 для функции u f x1 , x2 f (M ) двух независимых пере-
менных x1 , x2 обычно полагают x1 x , x2 y , u f x, y , имея в виду, что точка M (x, y) лежит на координатной плоскости xOy прямоугольной декартовой системы координат x, y, z . Более то-
го, если u z , то есть предположить, что значение u функции f определяет аппликату z , то уравнение z f x, y определяет поверхность в евклидовом пространстве R3 . Таков геометриче-
ский смысл функции двух независимых переменных. По тем же мотивам в пространстве R3 для функции трех независимых переменных вводят обозначение u f x, y, z . Однако эта функция не
имеет такую наглядную геометрическую интерпретацию как функция двух переменных. Рассмотрим несколько примеров функций многих (нескольких) переменных.
1. u 
 1 x2 y2 . Областью определения этой функции на плоскости xOy является круг с
1 x2 y2 . Областью определения этой функции на плоскости xOy является круг с
центром в начале координат радиуса |
1, а |
множество значений представляет собой отрезок |
|
0 u 1. Если u z , то уравнение z |
|
|
|
1 x2 |
y2 определяет полусферу радиуса 1 с центром в |
||
начале координат O(0,0,0) , расположенную в области z 0 . 2

2. u 
 x2 y2 9 1 . Областью определения этой функции является множество точек, ле-
x2 y2 9 1 . Областью определения этой функции является множество точек, ле-
жащих вне круга радиуса 3 с центром в начале координат, а множество значений представляет собой открытую полупрямую u 0 .
Предел функции многих переменных
Определение. Если каждому натуральному числу n поставлена в соответствие точка M n
евклидова пространства Rm , то говорят, что в этом пространстве определена последовательность точек M1 , M 2 , , M n , Эту последовательность обозначают также символом {M n }.
Определение. Последовательность {M n } точек пространства Rm называется сходящейся,
если существует точка A пространства Rm такая, что для любого положительного числа найдется номер N ( ) такой, что при n N выполняется неравенство (M n , A) . При этом точка A
называется пределом последовательности {M n }. |
|
|
||
Для |
предела |
A последовательности {M n } |
используются следующие |
обозначе- |
ния: lim M n |
A или M n |
A при n . |
|
|
n |
|
|
|
|
Существование предела последовательности {M n } означает, что в любой – окрестности |
||||
точки A находятся все точки последовательности {M n }, |
начиная с некоторого номера |
N , зави- |
||
сящего, вообще говоря, от . |
|
|
||
Пусть функция |
u f (M ) определена на множестве {M} точек евклидова пространства |
|||
Rm , а точка A пространства Rm является предельной точкой множества {M} .
Определение (по Гейне). Число b называется пределом функции u f (M ) в точке A , если для любой сходящейся к A последовательности {M n } точек множества {M} , все элементы M n которой отличны от A , соответствующая числовая последовательность значений функции { f (M n )} сходится к числу b .
Определение (по Коши). Число b называется пределом функции u f (M ) в точке A , если для любого положительного числа найдется положительное число ( ) такое, что для любой точки M из множества {M} , удовлетворяющей условию 0 (M , A) , справедливо неравенст-
во f (M ) b .
Для обозначения предела функции u f (M ) |
в точке A используются следующие обозна- |
||
чения: |
|
|
|
lim f (M ) b или |
lim |
f (x1 , x2 , , xm ) b , |
|
M A |
x1 |
a1 |
|
|
x2 |
a2 |
|
|
|
|
|
xm am
где ( a1 , a2 , , am ) – координаты точки A .
Оба определения предела функции эквивалентны, что доказывается точно так же, как и для функции одной переменной. Заметим, что в этих определениях не рассматривается значение функция u f (M ) в точке A .
Рассмотрим понятие предела функции u f (M ) при M . Предположим, что множество {M} , на котором задана функция u f (M ) , для любого 0 имеет точки, лежащие вне шара
радиуса с центром в точке O(0,0, ,0) . |
|
Определение (по Коши). Число b |
называется пределом функции u f (M ) при M , |
если для любого положительного числа |
найдется положительное число ( ) такое, что для всех |
точек M из множества {M} , удовлетворяющих условию (O, M ) , справедливо неравенство f (M ) b .
3
Для обозначения предела функции u f (M ) при M используется символ
lim f (M ) b .
M
Так же, как и для функции одной переменной, легко убедиться в том, что арифметические операции над функциями m переменных, имеющими предел в данной точке A (или при M ), приводят к функциям, также имеющим предел в точке A (соответственно при M ).
Сформулируем данное утверждение для предела в точке A .
Пусть две функции f (M ) |
и g(M ) |
определены на множестве {M} и имеют в точке A пре- |
|||||
делы, соответственно равные b и c . Тогда: |
|
|
|
|
|||
lim f (M ) g(M ) |
b c , |
lim |
f (M ) g(M ) b c , |
||||
M |
A |
|
|
M A |
|
|
|
lim |
f (M )g(M ) bc , |
lim |
f (M ) |
|
b |
при условии c 0 . |
|
|
|
||||||
M A |
|
M A g(M ) |
|
c |
|||
Определение. Функция |
u f (M ) называется бесконечно малой в точке A , если |
||||||
lim f (M ) 0 .
M A
Например, функция
f (M ) (x1 a1 )n1 (x2 a2 )n2 (xm am )nm ,
где n1 , n2 , , nm – положительные числа, является бесконечно малой в точке A(a1 , a2 , , am ) .
Если функция u f (M ) имеет в точке A предел равный b , то функция (M ) f (M ) b является бесконечно малой в точке A . Действительно,
lim (M ) lim [ f (M ) b] lim |
f (M ) lim b 0 . |
||
M A |
M A |
M A |
M A |
Отсюда следует, что если функция u f (M ) |
имеет предел b в точке A , то f (M ) b (M ) , где |
||
(M ) – бесконечно малая в точке A функция.
Сравнение бесконечно малых функций нескольких переменных проводится точно так же,
как для бесконечно малых функций одной переменной. Например, говорят, |
что функция f (M ) |
||||||
есть бесконечно малая высшего порядка по сравнению с функцией g(M ) |
при |
M A , если |
|||||
lim |
f (M ) |
0 , и в этом случае пишут |
f o(g) . Если же lim |
f (M ) |
b , где b 0 – конечное чис- |
||
|
|
||||||
M A g(M ) |
M A g(M ) |
|
|
||||
ло, то говорят, что функции f (M ) и |
g(M ) одного порядка при M A и пишут |
f O(g) или |
|||||
g O( f ) . |
|
|
|
|
|
||
Для функции u f (x1 , x2 , , xm ) нескольких переменных можно определить понятие предела по одной из переменных xk при фиксированных значениях остальных переменных. В связи с
этим возникает понятие повторного предела. Рассмотрим, например, функцию u f (x, y) |
двух |
|||||||||
переменных |
x и y , заданную в прямоугольной окрестности |
|
x x0 |
|
d1 , |
|
y y0 |
|
d2 |
точки |
|
|
|
|
|||||||
M 0 (x0 , y0 ) , |
за исключением, быть может, самой точки M 0 . Пусть для каждого фиксированного |
|||||||||
значения y , удовлетворяющего условию 0 |
|
y y0 |
|
d2 , |
существует предел функции u f (x, y) |
|
|
|
|||||
одной переменной x в точке x x0 , то есть |
|
|
||||
lim f (x, y) ( y) , |
|
|
||||
x x0 |
|
|
||||
и пусть, кроме того, существует предел b функции ( y) в точке y y0 |
|
|||||
lim ( y) b . |
|
|
||||
y y0 |
|
|
||||
В этом случае говорят, что существует повторный предел b для функции u f (x, y) |
в точке M 0 , |
|||||
который обозначается следующим образом: |
|
|
||||
lim lim f (x, y) b . |
(1) |
|||||
y y0 x x0
Аналогично определяется повторный предел
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim lim f (x, y) . |
|
|
|
|
|
|
|
|
(2) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 y y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Однако может оказаться, что оба повторных предела (1) и (2) существуют, но различны. |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
Пример. Вычислить повторные пределы (1) и (2) для функции f (x, y) |
x2 y2 x3 y3 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
в |
||||||||||||||||||||||||||||||||||
|
x2 y2 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точке O(0,0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∆ Подставляя заданную функцию f (x, y) в выражения (1) и (2), получаем |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
lim lim |
x2 y2 |
x3 y3 |
lim |
y2 y |
3 |
lim( 1 y) 1 , |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
|
|
|
|
y2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
y 0 x 0 |
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
y 0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
lim lim |
|
x2 y2 x3 y |
3 |
lim |
x2 x3 |
|
|
|
lim(1 x) 1. ▲ |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 |
|
|
|
|
x2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
x 0 y 0 |
|
|
|
|
|
|
|
x 0 |
|
|
|
|
x 0 |
|
|
|
|
|
||||||||||||||
|
|
|
Теорема. |
Пусть функция u f (x, y) |
|
определена в некоторой прямоугольной окрестности |
||||||||||||||||||||||||||||||||||
|
x x0 |
|
d1 , |
|
y y0 |
|
d2 точки M 0 (x0 , y0 ) |
и имеет в этой точке предел, равный b . Пусть также для |
||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
любого фиксированного x , 0 |
|
x x0 |
|
d1 |
|
существует предел (x) lim f (x, y) |
и для любого |
|||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y , 0 |
|
y y0 |
|
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y0 |
|
|
|
|
||||||
фиксированного |
|
|
существует предел ( y) lim f (x, y) . Тогда повторные преде- |
|||||||||||||||||||||||||||||||||||||
лы lim lim f (x, y) и lim lim f (x, y) существуют и равны b . |
x x0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
x x0 y y0 |
|
|
y y0 x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Отметим, что обратное утверждение неверно, то есть из существования и равенства по- |
|||||||||||||||||||||||||||||||||||||
вторных пределов еще не вытекает существование предела функции f (x, y) в точке M 0 (x0 , y0 ) . |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
Пример. Найти предел функции f (x, y) |
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
при M (x, y) O(0,0) . |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
x2 |
y2 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
∆ Очевидно, что оба повторных предела (1), (2) существуют и равны нулю: |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim lim f (x, y) lim f (0, y) 0 , |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0 x 0 |
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim lim f (x, y) lim f (x,0) 0 . |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 y 0 |
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
||||||
Однако lim f (x, y) не существует. Действительно, |
пусть точка M (x, y) стремится к точке O(0,0) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
M O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
по прямой y kx , проходящей через точку O . Тогда получим |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
xy |
|
|
lim |
|
|
kx2 |
|
|
|
|
k |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 |
|
|
(kx)2 |
1 k 2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
x 0 x2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( y kx) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Таким образом, приближаясь к точке O(0,0) по различным прямым, соответствующим раз- |
|||||||||||||||||||||||||||||||||||||
ным значениям |
k , получаем разные предельные значения. |
Отсюда следует, что предел данной |
||||||||||||||||||||||||||||||||||||||
функции в точке O(0,0) не существует, хотя повторные пределы существуют и равны. ▲ |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Непрерывные функции многих переменных |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
Рассмотрим функцию |
|
u f (M ) , |
заданную на некотором множестве {M} |
пространства |
|||||||||||||||||||||||||||||||||
Rm . Пусть A – некоторая предельная точка множества {M} , и пусть A принадлежит множеству
{M} .
Определение. Функция u f (M ) называется непрерывной в точке A , если предел этой функции в точке A существует и равен значению f ( A) .
Точки пространства Rm , в которых функция u f (M ) не обладает свойством непрерывности, называются точками разрыва этой функции.
Определение. Функция u f (M ) , определенная на множестве {M} , называется непрерывной на множестве {M} , если она непрерывна в каждой точке M этого множества.
5
Определение. Приращением или полным приращением функции u f (M ) в точке A назы-
вается функция u , определяемая равенством
u f (M ) f ( A) ,
где M – произвольная точка из области определения функции.
Пусть точки A и M имеют соответственно координаты a1 , a2 , , am и x1 , x2 , , xm . Обо-
значая приращения аргументов |
x1 x1 |
a1 , x2 x2 a2 ,…, |
xm xm am , получим для прира- |
||
щения функции u следующее выражение: |
|
|
|
||
u f (a1 x1,a2 x2 , , am xm ) f (a1,a2 , ,am ) . |
|
||||
Очевидно, для непрерывности функции u f (M ) в точке A необходимо и достаточно, |
|||||
чтобы ее приращение u представляло собой бесконечно малую в точке A функцию, то есть |
|||||
lim u lim ( f (M ) f ( A)) 0 или |
lim u 0 . |
(3) |
|||
M A |
M A |
|
x1 |
0 |
|
|
|
|
x2 |
0 |
|
|
|
|
|
|
|
|
|
|
xm 0 |
|
|
Условие (3) принято называть |
разностной формой |
условия непрерывности |
функции |
||
u f (M ) в точке A . |
|
|
|
|
|
Для функции u f (x1 , x2 , , xm ) |
можно определить понятие непрерывности по одной из |
||||
переменных при фиксированных значениях остальных переменных. Для введения такого понятия определим частные приращения функции u f (x1 , x2 , , xm ) в точке M (x1 , x2 , , xm ) , принадлежащей области определения функции.
Зафиксируем все аргументы, кроме xk , и придадим xk произвольное приращение xk такое, чтобы точка с координатами x1 , x2 , , xk xk , , xm находилась в области определения функции.
Определение. Частным приращением функции u f (M ) в точке M (x1 , x2 , , xm ) , соответ-
ствующим приращению xk аргумента xk , называется функция x |
u , определяемая равенством |
||
|
|
|
k |
x |
u f (x1 , x2 , , xk xk , , xm ) f (x1 , x2 , , xk , , xm ) . |
||
|
k |
|
|
Введем теперь понятие непрерывности функции u f (x1 , x2 , , xm ) по одной из перемен- |
|||
ных. |
|
|
|
Определение. |
Функция |
u f (x1 , x2 , , xm ) называется непрерывной в точке |
|
M (x1 , x2 , , xm ) по переменной xk |
, если частное приращение xk u этой функции в точке M пред- |
||
ставляет собой бесконечно малую функцию от xk .
Очевидно, из условия непрерывности функции u f (x1 , x2 , , xm ) в точке M вытекает непрерывность этой функции в данной точке по каждой из переменных x1 , x2 , , xm . Однако из непрерывности функции в точке M по каждой из переменных x1 , x2 , , xm не вытекает, вообще говоря, непрерывность этой функции в точке.
Пример. Исследовать на непрерывность функцию |
|
|
|||||||
|
x2 y |
|
, x4 |
y2 0, |
|||||
|
|
|
|
|
|||||
|
4 |
y |
2 |
||||||
u f (x, y) x |
|
|
|
|
|
|
|
||
|
|
0, |
|
x |
4 |
y |
2 |
0. |
|
|
|
|
|
|
|||||
∆ Заметим, что при любых значениях x и y справедливы равенства f (x,0) 0 , f (0, y) 0 , а, следовательно, частные приращения xu и y u функции u f (x, y) в точке O(0,0) при любых
x и y |
равны нулю. Таким образом, функция u f (x, y) в точке O(0,0) непрерывна как по x , |
так и по |
y . Пусть теперь точка M (x, y) стремится к точке O(0,0) по параболе y kx2 , проходя- |
щей через точку O . Тогда
6

lim |
x2 y |
lim |
x2 |
kx2 |
|
|
k |
. |
x4 y 2 |
x4 (kx2 )2 |
|
k 2 |
|||||
x 0 |
x 0 |
1 |
|
|||||
y 0 |
|
|
|
|
|
|
|
|
( y kx2 ) |
|
|
|
|
|
|
|
|
Таким образом, приближаясь к точке O(0,0) |
по различным параболам, соответствующим |
|||||||
разным значениям k , получаем разные предельные значения. Следовательно, предел функции u f (x, y) в точке O(0,0) не существует, а это означает, что функция разрывна в данной точке. ▲
Рассмотрим основные свойства непрерывных функций многих переменных. Доказательства этих свойств в основном аналогичны доказательствам соответствующих свойств функций одной переменной.
1. Арифметические операции над непрерывными функциями. Если функции f (M ) и g(M )
определены на множестве {M} и непрерывны в некоторой точке A этого множества, то функции
f (M ) g(M ) , f (M ) g(M ) , f (M ) так же непрерывны в точке A (в случае частного g( A) 0 ). g(M )
Данное свойство вытекает из соответствующего утверждения об арифметических операциях над функциями, имеющими предел.
2. Непрерывность сложной функции. Введем понятие сложной функции нескольких переменных. Пусть функции
|
|
|
|
|
x1 1 (t1 ,t2 , ,tk ), |
|
|
||||||||||
|
|
|
|
|
|
|
2 (t1 ,t2 , ,tk ), |
|
|
||||||||
|
|
|
|
|
x2 |
|
(4) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
m |
|
m |
(t ,t |
2 |
, ,t |
k |
) |
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
заданы на множестве {N} евклидова пространства Rk |
|
( t ,t |
2 |
, ,t |
k |
– координаты точек в этом про- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
странстве). Тогда с помощью формул (4) каждой точке N(t1 ,t2 , ,tk ) множества {N} ставится в |
|||||||||||||||||
соответствие точка M (x , x |
2 |
, , x |
m |
) |
евклидова пространства Rm . Обозначим через {M} множест- |
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
во всех таких точек. Пусть u |
f (x1 , x2 , , xm ) – функция m переменных, заданная на множестве |
|||||||
{M} . В этом случае говорят, |
что на множестве {N} евклидова пространства Rk определена |
|||||||
сложная функция u |
f (x1 , x2 , , xm ) , где x1 , x2 , , xm |
являются функциями переменных t1 ,t2 , ,tk |
||||||
и определяются соотношениями (4). |
|
|
|
|
||||
Теорема. Пусть функции x1 1 (t1 ,t2 , ,tk ) , x2 2 (t1 ,t2 , ,tk ) , …, |
xm m (t1 ,t2 , ,tk ) не- |
|||||||
прерывны в |
точке |
A(a1 , a2 , , ak ) , |
а функция |
u f (x1 , x2 , , xm ) |
непрерывна в |
точке |
||
B(b1 ,b2 , ,bm ) , где bi |
i (a1 , a2 , , ak ) , |
i 1,2, , m . Тогда сложная функция u f (x1 , x2 , , xm ) , |
||||||
где x1 , x2 , , xm |
представляют собой определенные здесь функции аргументов t1 ,t2 , ,tk , |
непре- |
||||||
рывна в точке A(a1 , a2 , , ak ) . |
|
|
|
|
|
|
||
3. Теорема (об устойчивости знака непрерывной функции). Если функция u f (M ) |
опре- |
|||||||
делена в окрестности точки |
A и непрерывна в точке A евклидова пространства Rm и если |
|||||||
f ( A) 0 , то существует такая |
– окрестность точки A , в пределах которой f (M ) не обращается |
|||||||
внуль и имеет знак, совпадающий со знаком f ( A) .
4.Теорема (о прохождении непрерывной функции через любое промежуточное значение). Пусть функция u f (M ) непрерывна во всех точках связного множества {M} евклидова про-
странства Rm , причем f ( A) и f (B) – значения этой функции в точках A и B этого множества. Пусть, далее, C – любое число, заключенное между f ( A) и f (B) . Тогда на любой непрерывной
7
кривой L , соединяющей точки A и B и целиком располагающейся в {M} , найдется точка N такая, что f (N) C .
5.Теорема (первая теорема Вейерштрасса). Непрерывная на замкнутом ограниченном множестве функция ограничена на этом множестве.
6.Определение. Точной верхней (нижней) гранью функции f (M ) на множестве {M} назы-
вается такое число |
|
|
|
(для нижней |
грани |
u ), которое удовлетворяет |
двум требованиям: 1) |
||||
u |
|||||||||||
f (M ) |
|
( f (M ) u ) для всех точек |
M множества {M} , 2) для любого 0 найдется хотя бы |
||||||||
u |
|||||||||||
одна точка M множества {M} , для которой |
f (M ) |
|
( f (M ) u ). |
|
|||||||
u |
|
||||||||||
Для обозначения точной верхней (нижней) грани функции f (M ) |
на множестве {M} ис- |
||||||||||
пользуют обозначения |
|
sup f (M ) ( u inf |
f (M ) ). |
|
|||||||
u |
|
||||||||||
|
|
|
|
|
|
{M } |
{M } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема (вторая теорема Вейерштрасса). Непрерывная на замкнутом ограниченном множестве функция достигает на этом множестве своих точных верхней и нижней граней.
7. Определение. Функция u f (M ) называется равномерно непрерывной на множестве {M} евклидова пространства Rm , если для любого положительного числа существует такое по-
ложительное , зависящее только от , что для любых двух |
точек M и M множества, удовле- |
|||
творяющих условию (M , M ) , выполняется неравенство |
|
f (M ) f (M ) |
|
. |
|
|
|||
|
|
|
|
|
Теорема (Кантора). Непрерывная на замкнутом ограниченном множестве функция равномерно непрерывна на этом множестве.
Теорема Кантора доказывается аналогично теореме о равномерной непрерывности для функции одной переменной.
Частные производные. Дифференцируемость функций многих переменных
Пусть M (x1 , x2 , , xm ) – внутренняя точка области определения функции u f (x1 , x2 , , xm ) . Рассмотрим в данной точке отношение частного приращения xk u к соответствующему приращению xk аргумента xk :
|
|
|
|
|
|
x |
k |
u |
|
f (x , x |
2 |
, , x |
k |
x |
k |
, , x |
m |
) f (x , x |
2 |
, , x |
k |
, , x |
m |
) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Полученное отношение представляет собой функцию от переменной xk , |
определенную |
||||||||||||||||||||||||||||||||||
для всех отличных от нуля значений xk , для которых точка M (x1 , x2 , , xk |
xk , , xm ) принад- |
||||||||||||||||||||||||||||||||||
лежит области определения функции u |
f (x1 , x2 , , xm ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Определение. Если существует предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
u |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk 0 x |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то он называется частной производной функции |
u f (x1 , x2 , , xm ) |
|
по переменной xk |
в точке |
|||||||||||||||||||||||||||||||
M (x , x |
|
, , x |
|
) |
и обозначается любым из следующих символов: |
u |
, |
|
f |
, |
|
u , |
f . |
|
|||||||||||||||||||||
2 |
m |
|
|
|
|
||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xk |
|
|
|
xk |
|
|
xk |
|
xk |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отметим, |
что при |
фиксированных значениях |
всех |
|
аргументов, |
|
кроме |
xk , |
функция |
||||||||||||||||||||||||||
u f (x1 , x2 , , xm ) становится функцией одной переменной. Производная этой функции одной переменной и есть частная производная функции u f (x1 , x2 , , xm ) по аргументу xk . Поэтому вы-
числение частных производных производится по тем же правилам, что и вычисление производных функций одной переменной.
8
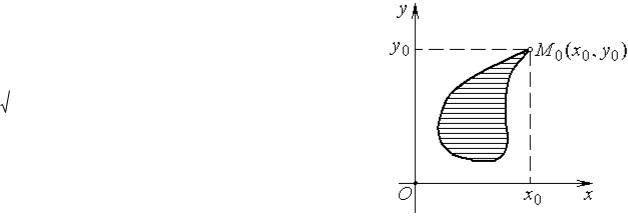
Пример. Найти частные производные от функции u 4x3 y x2 |
2y3 . |
|
||||
∆ При вычислении частной производной |
u функции u f (x, y) |
считаем, что y |
есть по- |
|||
|
x |
|
|
|
||
стоянная величина, и, следовательно, u f (x, y) |
зависит от одной переменной x . Применяя пра- |
|||||
вила дифференцирования функции одной переменной. Получаем |
|
|
|
|||
u 12x2 y 2x . |
|
|
|
|||
x |
|
|
|
|
|
|
|
|
u |
|
x постоянная, |
|
|
Если же находится частная производная |
|
, то полагаем, |
что |
и тогда |
||
y |
||||||
u f (x, y) зависит от одной переменной y . Следовательно, |
|
|
|
|||
u 4x3 |
6 y2 . ▲ |
|
|
|
||
y |
|
|
|
|
|
|
Замечание 1. Из существования у функции в данной точке всех частных производных, вообще говоря, не вытекает непрерывность функции в этой точке. Действительно, функция
|
|
|
xy |
|
при |
x2 |
y2 |
0, |
||
|
|
|
||||||||
|
2 |
|
2 |
|||||||
y |
|
|
|
|
|
не имеет предела в точке O 0, 0 , а, следовательно, не является |
||||
u x |
|
|
|
|
|
|
|
|||
|
|
0 |
|
при |
x |
2 |
y |
2 |
0 |
|
|
|
|
|
|
||||||
непрерывной в этой точке. Однако, данная функция имеет частные производные по переменным x и y в точке O 0, 0 . Это следует из того, что f (x,0) 0 , f (0, y) 0 , и поэтому
u |
|
0 , |
u |
0 . |
|
||||
x |
|
y |
||
|
(0,0) |
(0,0) |
||
|
||||
|
|
|
Замечание 2. Отметим, что определение частных производных всегда применимо для внутренних точек области определения функции, но для граничных точек этой области, вообще говоря, непригодно. В частности, это связано с тем, что в граничных точках области определения функции не всегда можно вычислить частные приращения функции. В качестве примера можно рассмотреть граничную точку M 0 области, изображенной на рис. 1. В связи с этим принято опре-
делять частные производные в граничных точках как пределы этих производных при стремлении точек к границе.
Определение. |
Функция |
u f (x1 , x2 , , xm ) |
называется дифференцируемой в |
точке |
||||
M (x1 , x2 , , xm ) , если ее полное приращение в этой точке может быть представлено в виде |
|
|||||||
|
|
|
u A1 x1 A2 x2 Am xm 1 x1 2 x2 m xm , |
(5) |
||||
где A1 , A2 , , Am |
– некоторые не зависящие от x1 , x2 ,…, xm числа, 1 , 2 , , m – бесконечно |
|||||||
малые функции при x1 0 , x2 |
0 ,…, xm 0 , равные нулю при x1 x2 xm 0 . |
|||||||
Соотношение (5) называется условием дифференци- |
|
|||||||
руемости функции в данной точке M . Условие (5) |
диффе- |
|
||||||
ренцируемости функции можно записать также в другой эк- |
|
|||||||
вивалентной форме |
|
|
|
|
|
|
||
|
u A1 x1 A2 x2 Am xm o( ) , |
(6) |
|
|||||
|
|
|
|
|
|
|
||
где |
x2 x2 x2 . |
|
|
|
|
|||
|
1 |
2 |
m |
|
|
|
|
|
Теорема. |
Если функция |
u |
f (x1 , x2 , , xm ) |
диффе- |
|
|||
ренцируема в точке M (x1 , x2 , , xm ) , |
то она и непрерывна в |
|
||||||
этой точке. |
|
|
|
|
|
|
|
|
Обратное утверждение неверно, то есть непрерыв- |
|
ность является только необходимым, но не достаточным ус- |
|
ловием дифференцируемости функции. |
Рис 1. |
|
|
9 |
|

Заметим, что, если для функции одной переменной существование производной в точке является необходимым и достаточным условием дифференцируемости функции в этой точке, то для функции нескольких переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами функции.
Теорема (необходимое условие дифференцируемости функции). Если функция u f (x1 , x2 , , xm ) дифференцируема в точке M (x1 , x2 , , xm ) , то в этой точке существуют част-
ные производные по всем аргументам, причем u Ai , где Ai определяются из условия (5) или
xi
(6) дифференцируемости функции.
Следствие 1. Условие (6) дифференцируемости функции в точке M можно записать в виде
u |
u |
x |
u |
x |
|
|
|
u |
x |
|
o( ) . |
|
|
2 |
|
m |
|||||||
|
1 |
x2 |
|
|
xm |
|
|||||
|
x1 |
|
|
|
|
|
|||||
Следствие 2. Если функция u f (x1 , x2 , , xm ) |
дифференцируема в точке M (x1 , x2 , , xm ) , |
||||||||||
то представление ее приращения u в форме (5) или (6) единственно. |
|||||||||||
Теорема (достаточные |
условия |
дифференцируемости функции). Если функция |
|||||||||
u f (x1 , x2 , , xm ) имеет частные производные по всем аргументам в некоторой окрестности точки M 0 (x10 , x20 , , xm0 ) , и в этой точке все эти частные производные непрерывны, то данная функция дифференцируема в M 0 .
Полный дифференциал функции многих переменных. Геометрический смысл полного дифференциала
Определение. Дифференциалом du (полным или первым дифференциалом) дифференци-
руемой в точке M (x1 , x2 , , xm ) функции u f (x1 , x2 , , xm ) называется линейная относительно приращений аргументов часть приращения этой функции в точке M . Если все коэффициенты Ai
в представлении (5) приращения дифференцируемой функции равны нулю, то дифференциал du функции в точке M считается равным нулю.
Таким образом, дифференциалом du дифференцируемой в точке M |
функции |
u f (x1 , x2 , , xm ) называется выражение |
|
du A1 x1 A2 x2 Am xm . |
(7) |
Используя теорему о необходимом условии дифференцируемости функции, можно переписать выражение (7) для полного дифференциала du следующим образом:
du |
u |
x |
|
u |
|
x |
|
|
u |
x |
|
. |
|
|||||
|
|
|
|
2 |
|
|
m |
|
||||||||||
|
x1 |
1 |
x2 |
|
|
|
|
xm |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Дифференциалом независимой переменной |
xi будем называть приращение этой перемен- |
|||||||||||||||||
ной dxi xi . Тогда формулу для полного дифференциала можно записать в виде |
|
|||||||||||||||||
du |
|
u |
dx |
u |
|
dx |
|
|
|
u |
dx |
|
|
. |
(8) |
|||
|
|
|
|
2 |
|
|
m |
|||||||||||
|
|
x1 |
1 |
|
x2 |
|
|
|
|
xm |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Формула (8) является справедлива и в том случае, когда аргументы x1 , x2 , , xm являются дифференцируемыми функциями некоторых новых переменных t1 ,t2 , ,tk , которые можно счи-
тать независимыми. Указанное свойство называется свойством инвариантности формы первого дифференциала.
Напомним, что дифференциал функции одной переменной геометрически представляет собой приращение ординаты касательной к графику функции в данной точке. Аналогично можно рассмотреть геометрический смысл дифференциала для функции двух переменных. Введем сначала понятие касательной плоскости к поверхности в точке.
10
