3.2. Метод Зейделя.
Более
быструю сходимость метода простых
итераций можно обеспечить, если для
каждой
-ой
компоненты вектора решения
приближения использовать предыдущие
компоненты от 1 до
также
приближения, а остальные компоненты от
до
используются от предыдущего
-го
приближения. Такая модификация метода
простых итераций носит название «метода
Зейделя». Запишем рабочие формулы метода
Зейделя для каждой компоненты:
.
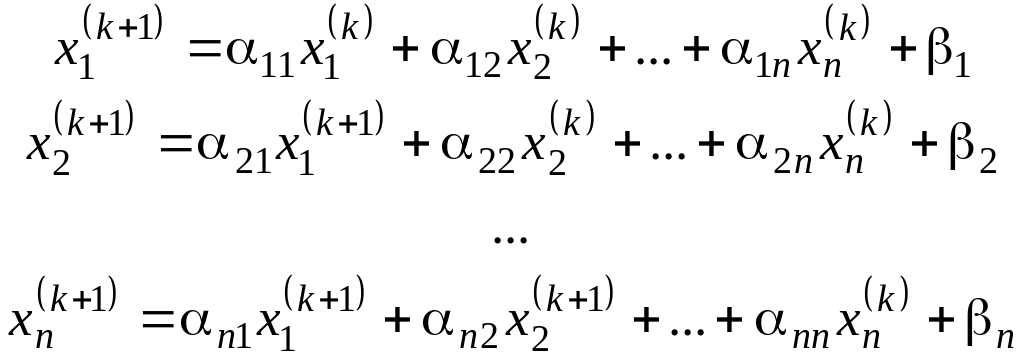Первое и второе достаточные условия для сходимости метода простых итераций будут одновременно достаточными и для процесса Зейделя.
При использовании итерационных методов для решения систем ошибка вычислений в большинстве случаев эквивалентна некоторому ухудшению очередного приближения. Это отразится только на числе итераций, а не на точности окончательного результата.
4. ИнтерполиРование функций
Задача интерполяции функций возникает в тех случаях, когда:
функция задана в виде таблицы, и необходимо знать значения функции для промежуточных значений аргументов, расположенных в таблице между узлами
,
а также для аргументов, расположенных
вне таблицы;
известна лишь таблица функции и требуется определить ее аналитическое выражение;
известно аналитическое выражение функции, но оно имеет очень сложный вид, вследствие чего возникает необходимость представления этой функции в более простом виде. Например, при вычислении определенных интегралов вида
можно заменить подынтегральную функцию
некоторой приближенной функцией
в виде многочлена. Тогда
.
Построив интерполяционный многочлен любого вида также можно расширить таблицу как влево, так и вправо, вычисляя построенный многочлен в точках, не принадлежащих таблице (задача экстраполяции). Кроме того, построив интерполяционных многочлен, можно уплотнить таблицу, определяя значения функции для промежуточных аргументов между узловыми точками.
4.1. Интерполяционная формула Лагранжа.
Пусть задана система точек
,
в которых известны значения функции
.
То есть, задана следующая таблица
-
…
…
Установим зависимость
одного ряда чисел от другого и построим
новую функцию, которая с определенной
степенью точности будет приближена к
заданной.
Рассмотрим пример построения
интерполяционного многочлена Лагранжа
по заданной системе точек (в общем случае
для неравноотстоящих аргументов).
Построим некоторый многочлен
таким образом, чтобы его значения совпали
со значениями функции, заданными в
таблице, для тех же аргументов, то есть
.
Лагранж предложил строить многочлен
степени в виде:
.
Здесь в каждом слагаемом отсутствует
скобка
,
которой соответствует коэффициент
.
Найдем неизвестные коэффициенты
,
называемые коэффициентами Лагранжа,
используя условие
:
При
:
.
.
Следовательно, коэффициент
вычисляется по следующей формуле:
При
:
.
.
Следовательно, коэффициент
вычисляется по следующей формуле:
.
Значения остальных коэффициентов вычисляются аналогично.
С учетом найденных коэффициентов интерполяционный многочлен Лагранжа запишется в виде
Остаточный член формулы:
,
где - точка наименьшего промежутка, содержащего все узлы и точку .
Пример. По заданной системе точек
|
|
|
|
|
0.5 |
0.707 |
1.0 |
построить интерполяционный многочлен Лагранжа второго порядка вида:
Коэффициенты этого многочлена будут вычислены по формулам вида:
Тогда многочлен Лагранжа второго порядка будет иметь вид:
.
Учитывая, что таблица приведена для
функции
,
вычисленной в контрольных точках
,
сравним погрешность вычислений данной
функции и построенного многочлена в
контрольной точке
:
и
.
Погрешность вычислений, по сравнению с истинным значением, составляет
.
Н
иже
приведены графики синусоиды и построенного
многочлена Лагранжа на заданном
интервале. Из графика видно, что многочлена
второго порядка достаточно для обеспечения
необходимой точности воспроизводимой
синусоиды.