1.4. Метод Ньютона (метод касательных).
Пусть уравнение (1) имеет на интервале
единственный корень, причем существует
непрерывная на
производная
.
Метод Ньютона служит для уточнения
корней нелинейных уравнений в заданном
интервале. Его можно рассматривать как
частный случай метода простых итераций,
если
.
Тогда итерационный процесс осуществляется
по формуле:
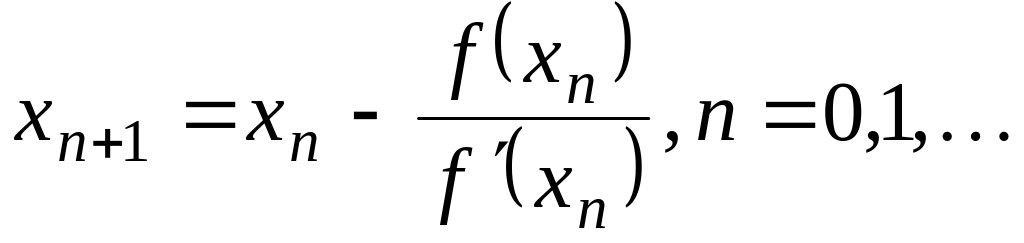(5)
Г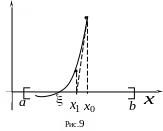
еометрически
(Рис.9) этот процесс означает замену на
каждой итерации графика кривой
касательной к ней в точках
.
Достаточное условие сходимости
обеспечивается выбором начальной точки
.
Начальным приближением
служит один из концов отрезка
,
в зависимости от того, в каком из них
выполняется достаточное условие
сходимости
(6)
При произвольном начальном приближении итерации сходятся, если
.
Метод Ньютона рекомендуется применять для нахождения простых действительных корней уравнения (1).
Достоинством метода является то, что он обладает быстрой скоростью сходимости, близкой к квадратичной. Недостатки метода:
- не при любом начальном приближении
метод Ньютона сходится, а лишь при том,
для которого
.
- если
,
то
.
- если
,
то
.
Последних трудностей можно избежать, применив модификацию метода Ньютона, рабочая формула при этом имеет вид
.
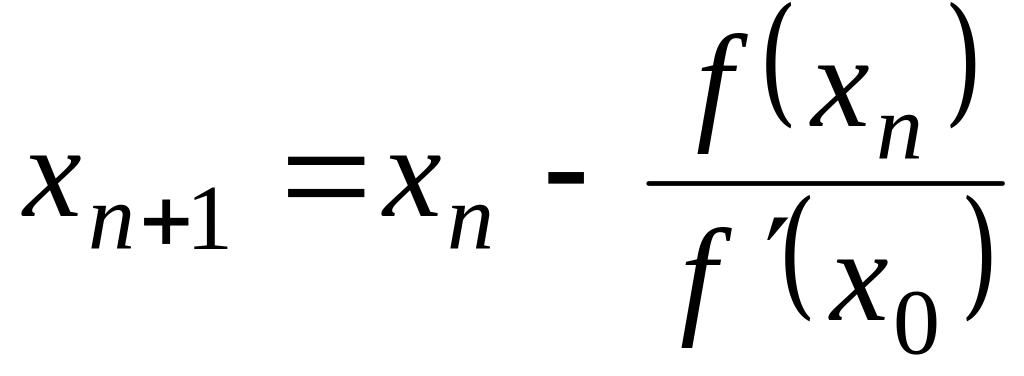2. Решение систем нелинейных уравнений.
Система нелинейных уравнений имеет вид:
(7)
Здесь
- неизвестные переменные, а система (7)
называется нормальной системой порядка
,
если хотя бы одна из функций
нелинейна.
Решение систем нелинейных уравнений – одна из трудных задач вычислительной математики. Трудность состоит в том, чтобы определить: имеет ли система решение, и, если – да, то сколько. Уточнение решений в заданной области – более простая задача.
Пусть функции
определены в областях
.
Тогда область
и будет той областью, где можно найти
решение. Наиболее распространенными
методами уточнения решения являются
метод простых итераций и метод Ньютона.
2.1. Метод простых итераций для решения систем нелинейных уравнений.
Из исходной системы (7) путем эквивалентных преобразований переходим к системе вида:
(8)
Итерационный процесс, определяемый формулами
,
можно начать, задав начальное приближение
.
Достаточным условием сходимости
итерационного процесса является одно
из двух условий:
или
.
Распишем первое условие:
при
при
.
Распишем второе условие:
при
при
.
Рассмотрим один из способов приведения системы (7) к виду (8), допускающему сходящиеся итерации.
Пусть задана система второго порядка вида:
.
Требуется привести ее к виду:
.
Умножим первое уравнение системы на
неизвестную постоянную
,
второе - на
,
затем сложим их и добавим в обе части
уравнения
.
Получим первое уравнение преобразованной
системы
где
.
Далее, умножим первое уравнение системы
на неизвестную постоянную
,
второе - на
,
затем сложим их и добавим в обе части
уравнения
.
Тогда второе уравнение преобразованной
системы будет иметь вид
где
.
Неизвестные постоянные
определим из достаточных условий
сходимости
и
.
Запишем эти условия более подробно:
Полагая равными нулю выражения под знаком модуля, получим систему из четырех уравнений с четырьмя неизвестными для определения постоянных :
.
При таком выборе параметров условия
сходимости будут соблюдены, если частные
производные функций
и
будут изменяться не очень быстро в
окрестности точки
.
Чтобы решить систему, нужно задать
начальное приближение
и вычислить значения производных
и
,
в этой точке. Вычисление
осуществляется на каждом
шаге итераций, при этом
,
,
.
Метод простых итераций является самоисправляющимся, универсальным и простым для реализации на ЭВМ. Если система имеет большой порядок, то применение данного метода, имеющего медленную скорость сходимости, не рекомендуется. В этом случае, используют метод Ньютона, который имеет более быструю сходимость.