7. Краевые задачи для Дифференциальных Уравнений второго порядка.

Пример 1. Рассмотрим простейшую двухточечную краевую задачу.

Найти функцию , удовлетворяющую дифференциальному уравнению второго порядка вида:

(40)

и принимающую при и заданные значения . Геометрически (Рис.10) это означает, что требуется найти интегральную кривую, проходящую через данные точки и .

Пример 2. Найти такое решение дифференциального уравнения (40), чтобы производные имели заданное значение . Геометрически (Рис.11) это сводится к отысканию интегральной кривой, пересекающей прямые и под заданными соответственно углами и такими, что и .

7.1. Решение краевой задачи для обыкновенного дифференциального уравнения второго порядка методом конечных разностей.

Рассмотрим двухточечную краевую задачу для линейного дифференциального уравнения. Найти решение уравнения

(41)

с дополнительными краевыми условиями

(42)

где числа считаются известными и

,

то есть одна из величин не равна нулю.

Коэффициенты являются непрерывными функциями на некотором отрезке . Решением этого уравнения является некоторая непрерывная на функция , имеющая первую и вторую производные на , удовлетворяющая исходному уравнению и дополнительным краевым условиям.

Поставленная краевая задача решается с помощью перехода от исходной задачи к новой, записанной в конечно-разностной форме. Тогда решение новой задачи будет являться приближенным решением исходной задачи. В силу того, что первая и вторая производные, входящие в уравнение и в краевые условия, будут заменены приближенными конечно-разностными формулами, решения с применением метода конечных разностей получается не в виде непрерывной функции , а виде таблицы ее значений в отдельных точках (Рис.12). Для этого разобьем на частей так, чтобы . Наша задача – найти значения функции в точках . Для того, чтобы перейти от исходной задачи к конечно-разностной, надо получить формулы для представления первой и второй производных в конечно-разностном виде. Они получаются, если применить разложение функции в окрестности некоторой точки в ряд Тейлора, ограничиваясь вторыми производными:

.

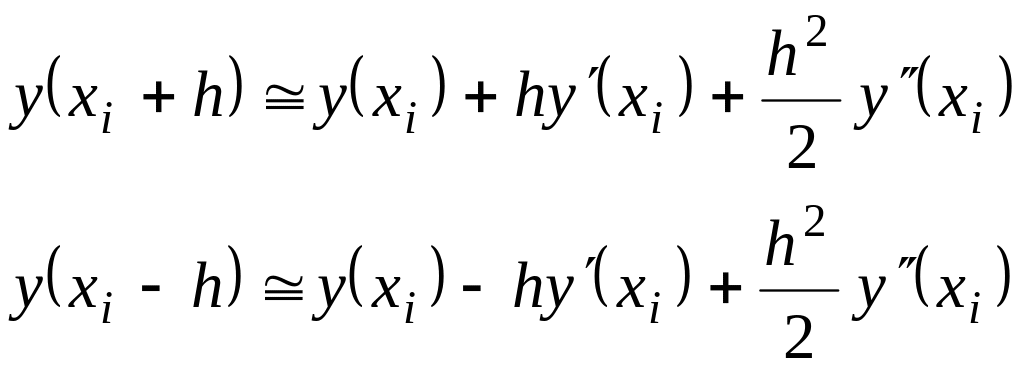Складываем эти ряды и получаем выражение второй производной в конечно-разностной форме:

.

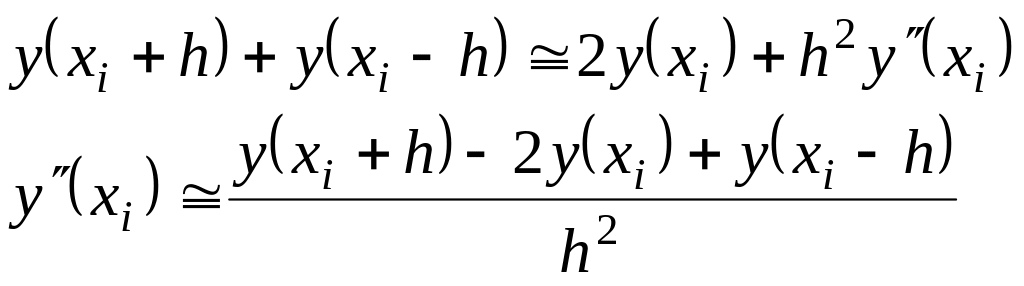Аналогично получим формулу для первой производной, если вычтем ряды:

.

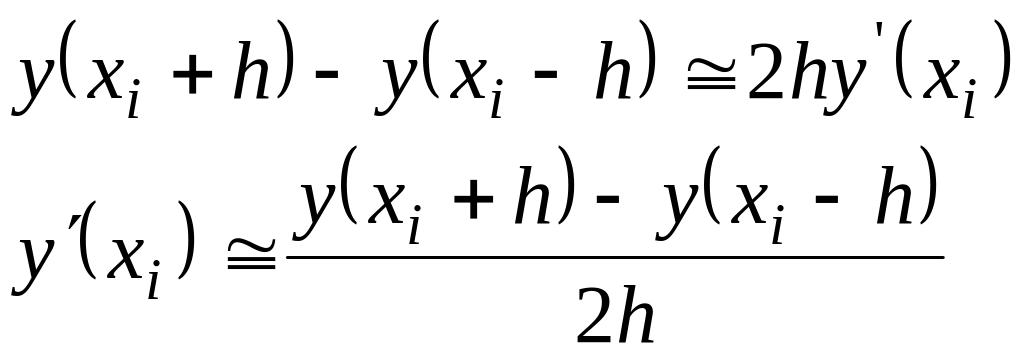Обозначим: . .

С учетом введенных обозначений запишем исходное уравнение для узловых точек :

, (43)

Представим

;

;

в конечно-разностной форме, тогда к системе (43) добавляется еще два уравнения, соответствующие краевым условиям:

(44)

(45)

Получили систему линейных алгебраических уравнений (43) – (45) с неизвестными . Решив эту систему любым известным методом, получим приближенное решение для исходной задачи.

Заметим, что система представляет собой систему с разряженной матрицей, имеющей трехдиагональный вид. Поэтому, для решения системы применяют специальные методы, позволяющие оперировать только с элементами матрицы, отличными от нуля. Одним из таких методов является метод прогонки.

7.2. Метод прогонки.

Запишем систему (45) в канонической форме:

,

, .

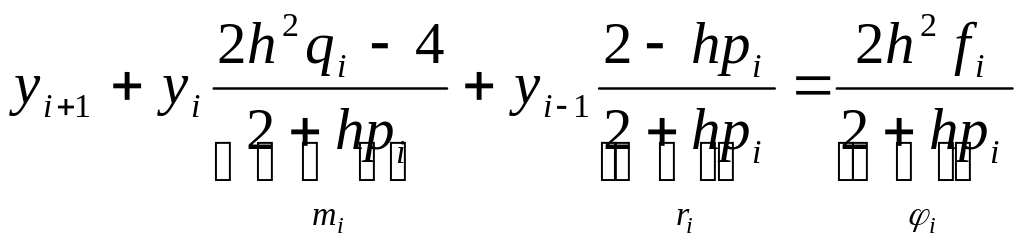Получим:

, . (46)

Будем искать в виде:

. (47)

где коэффициенты требуется определить. Выразим и подставим в исходную систему (46):

.

Выразим из последнего выражения :

.

Сравнивая полученную формулу с (47), получим выражения для :

(48)

Чтобы начать расчеты по этим формулам, надо знать . Найдем их из первого краевого условия. Выражая и сравнивая с , получим ; .

Итак, вычисления, называемые прямым ходом, осуществляют в следующем порядке:

1. Вычисляют значения .

2. Находят .

3. Вычисляют , .

Обратный ход вычислений состоит в следующем:

1. Решают систему из двух уравнений относительно и :

и получают .

2. Вычисляют , начиная с и далее до .

3. Находят .

В результате работы алгоритма получим значения исходной функции в узловых точках , т.е. получим таблицу значений функций, которая является приближенным решением исходной задачи. Используя полученную таблицу, можно построить аналитический вид функции. Как правило, эту функцию строят в виде многочлена.

Для оценки погрешности метода конечных разностей применяют двойной пересчет с шагом и . Приближенная оценка погрешности значения получается по формуле , где - значение точного решения краевой задачи в точке : и - значения в точке , полученные соответственно с шагом и .