2.6. Задания
Исследовать
решение логистического уравнения,
описывающего процесс изменения
численности популяции . Во всех вариантах
начальное значение времени
,
конечное –
(или то значение, при котором уменьшающиеся
параметры остаются положительными).
Параметры
,
и
– значения параметров в начальный
момент времени
.
Если нет указаний по изменению какого-либо
параметра, то параметр остается равным
начальному значению. Во всех вариантах
получить решение при начальных значениях
параметров и при изменениях параметров.
Построить графики всех решений и
изменений заданных параметров.
Вариант |
|
|
|
|
|
Исследовать |
1 |
3 |
1 |
0,00050 |
1000 |
0 |
Изменение
с
шагом
|
2 |
4 |
0,5 |
0,00050 |
1200 |
0 |
Изменение
с
шагом
|
3 |
5 |
1 |
0,00025 |
1300 |
0 |
Изменение
с
шагом
|
4 |
6 |
0,5 |
0,00025 |
1500 |
0 |
Изменение
с
шагом
|
5 |
3 |
1 |
0,00050 |
2000 |
0 |
Изменение
с
шагом
|
6 |
4 |
0,5 |
0,00050 |
1000 |
0,000050 |
Изменение
с
шагом
|
7 |
5 |
1 |
0,00025 |
1200 |
0,000025 |
Изменение
с
шагом
|
8 |
6 |
0,5 |
0,00025 |
1300 |
0,000010 |
Изменение
с
шагом
|
9 |
3 |
1 |
0,00050 |
1500 |
0,000010 |
Изменение с шагом |
10 |
4 |
0,5 |
0,00050 |
2000 |
0,000010 |
Изменение с шагом |
3. Исследование модели лотки‑вольтерры
3.1. Цель работы
Исследование моделей сотрудничества и борьбы за существование.
3.2. Постановка задачи
Рассмотрим простейшую модель взаимодействия двух популяций – хищников, например, волков, и жертв, например, зайцев. Модель описывается системой дифференциальных уравнений
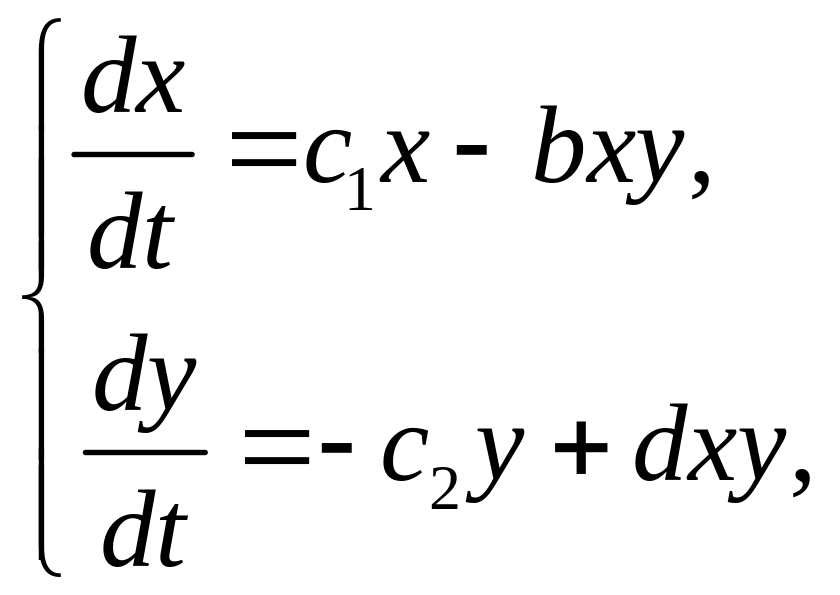
где – численность жертв, – численность хищников.
Член
в первом уравнении характеризует
естественный прирост жертв, пропорциональный
численности жертв. Член
означает убыль жертв из‑за встреч с
хищниками (таких встреч не более
).
Член
во втором уравнении характеризует
естественную убыль хищников, а член
– прирост численности хищников,
питающихся жертвами. Модель не учитывает
естественную смертность жертв,
ограниченность экологической ниши и
внутривидовую конкуренцию.
Система
решается при начальных условиях:
.
Система
имеет стационарные, т. е. не зависящие
от времени решения, которые получаются
приравниванием нулю производных по
времени:
и
.
Формулы Эйлера для решения системы
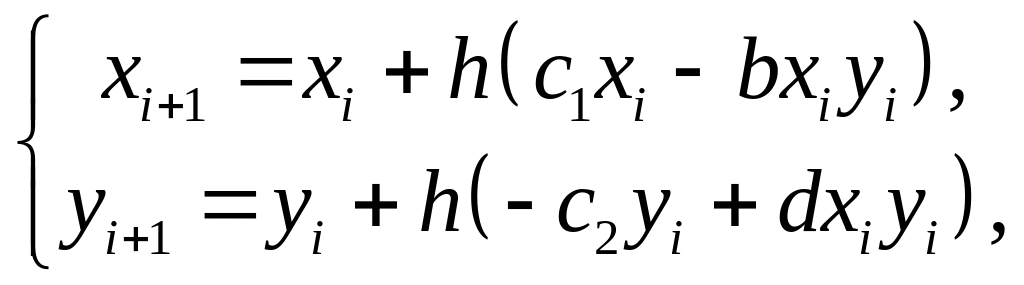
где – шаг по времени.
Следует учесть, что система представляет собой так называемую жесткую систему, т. е. система очень чувствительна к изменениям исходных данных и погрешностям вычислений. Для жестких систем разработаны специальные методы решения. Нас не интересует высокая точность решения, поэтому будем использовать метод Эйлера, но с малым шагом .