66

I. Элементы теории вероятности.

Вероятность – понятие, относящееся к случайным процессам. Физический процесс является случайным, если при повторных измерениях некоторого параметра процесса (при неизменных условиях) его величина (хаотично, непредсказуемо) принимает значение из некоторого интервала (множества) значений. Такой параметр называется случайным (случайной физической величиной).

Случайная величина может быть дискретной или непрерывной.

В зависимости от схемы измерений вероятность может быть определена как «частотная» или «временная». Вероятность того, что дискретная величина x при однократном измерении будет иметь значение x_{i ,} определяется формулой

- это формула частотного определения вероятности. N – число «измерений», n_i – число измерений, при которых случайная величина x принимала значение x_i.

- это формула временного определения вероятности. t_i – время в течение, которого система находилась в состоянии, при котором случайная величина x принимала значение x_i, T – полное время наблюдения системы.

Для непрерывной величины приведенные формулы должны быть переписаны в виде

, .

Здесь n₁₂ – число измерений, в которых значение измеряемого параметра было заключено в интервале (x₁ – x₂), t₁₂ – время, в течение которого значение измеряемого параметра было заключено в интервале (x₁ – x₂).

Для непрерывной величины функция вероятности может быть записана в виде интеграла

.

- функция плотности вероятности.

- дифференциальная вероятность (вероятность величины при однократном измерении иметь значение в бесконечно малом интервале (x, x + dx)).

 Задача. Определите функции плотности вероятности координаты, скорости и энергии для «гравитационного кузнечика». (Частица падает вертикально с некоторой высоты и упруго отражается от «плиты».)

Для решения задачи используем временное определение дифференциальной вероятности .

Здесь dt - время пролета частицей интервала dy, расположенного на высоте h – y. T – время падения до отметки h (половина периода движения). Далее используем элементарные формулы кинематики свободного падения

, .

Для упрощения положим m = 1, g = 1, h = 1. Тогда

.

Т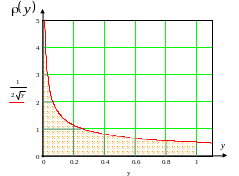 аким образом .

График функции плотности вероятности координаты y

Площадь под графиком в интервале (0-1) равна 1 в соответствии с условием нормировки.

Теперь определим функцию плотности вероятности для скорости падающей частицы. Для этого преобразуем дифференциальную вероятность к новой переменной, используя соотношение между скоростью и координатой¹

.

Отсюда получаем, что функция плотности вероятности для скорости есть константа. С учетом двузначности обратной функции , эту константу удобнее искать из условия нормировки

Таким образом, функция плотности вероятности для скорости записывается в виде

.

Ее график.

П ри движении полная энергия частицы сохраняется, поэтому энергетическая функция плотности вероятности падающей частицы имеет вид функции Дирака (  = 1)

График функции энергетической плотности вероятности.

Для аппроксимации (построения графика) дельта функции использована зависимость

.

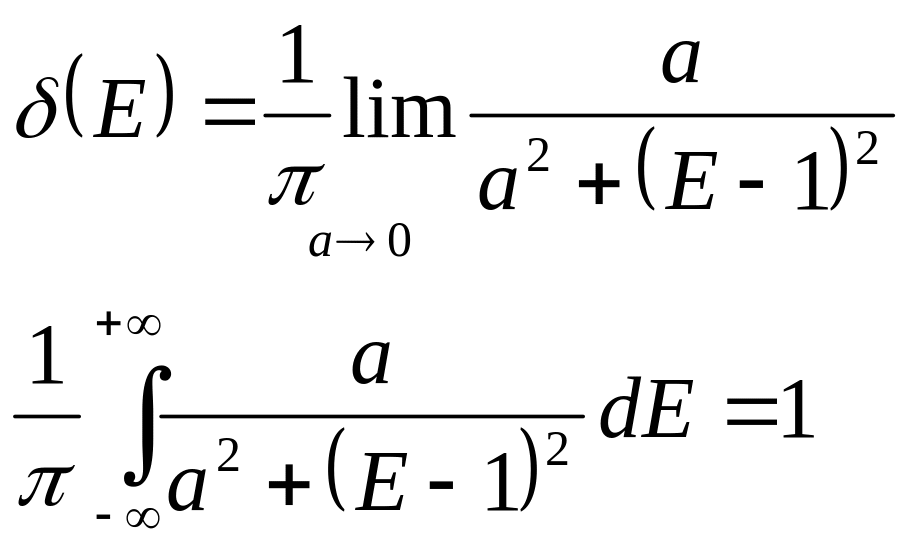Примеры функций вероятности.

1. Биномиальное распределение   (дискретное распределение).

Эта функция определяет вероятность при N испытаниях получить n «благоприятных» событий². Биномиальное распределение содержит один параметр p – вероятность события при однократном испытании (измерении).

Г рафик функции вероятности биномиального распределения при N = 10, p = 0,3.

Г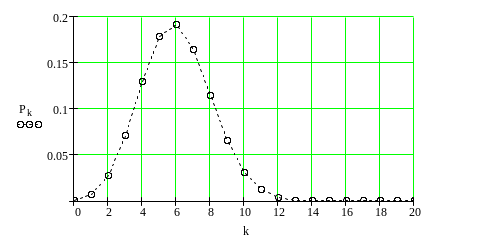 рафик функции вероятности биномиального распределения при N = 20, q = 0,3.

На графиках видно, что вероятность максимальна при средних значениях .

 Упражнение. Покажите, что при N стремящимся к бесконечности и при постоянной величине p биномиальное распределение переходит в распределение Гаусса.

2. Распределение Пуассона (дискретное распределение).³

Это распределение определяет вероятность n «благоприятных» событий на интервале

времени t . Функция определена одним параметром - средним значением числа

событий на единичном интервале времени.

Распределение Пуассона при . Максимумы функций распределения наблюдаются при средних значениях .

3. Нормальное распределение (функция плотности вероятности)

.

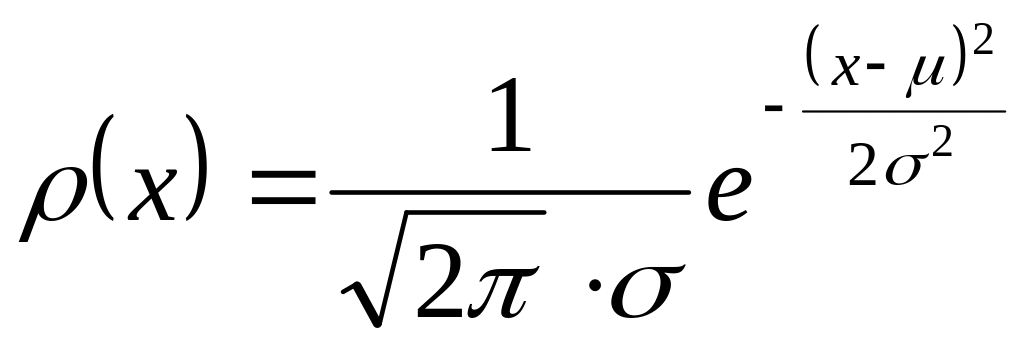О дно из наиболее важных распределений. Определено двумя параметрами:  - среднее значение, ² - дисперсия. Смысл распределения можно пояснить на основе статистики среднего значения. Пусть имеется случайная величина x. Произведено n измерений (определены x_i). Вычислено «выборочное среднее» . Центральная предельная теорема теории вероятности утверждает, что выборочное среднее (при n  ) распределено по нормальному закону. При этом распределение самой величины x может быть любым.

График нормального распределения при нулевом среднем и единичной дисперсии.

2. Основные положения феноменологической термодинамики.

1. Термодинамическая система. Температура.

Система, в которой определена температура (как один из параметров состояния), является термодинамической системой. Это утверждение может считаться «нулевым» началом термодинамики.⁴

О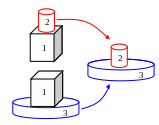 пределение температуры базируется на понятии теплового равновесия термодинамической системы и его транзитивности.

В общем виде равновесие двух термодинамических систем, находящихся в тепловом контакте определяется некоторой функцией набора параметров двух систем

.

В соответствии со схемой транзитивности можно записать

Можно показать, что этой схеме уравнений удовлетворяет только «разностный» вид функции

Или

.

Отсюда следует уравнение

,

которое является уравнением равновесия термодинамической системы. Тепловое равновесие двух систем определяется равенством для этих систем параметров . Этот параметр  и можно принять за меру температуры. Измерение температуры осуществляется термометром – малой термодинамической системой, которую приводят в тепловой контакт с измеряемой системой. Для построения шкалы температур можно использовать любой параметр «термометра», который является функцией температуры.

Считается, что для логического определения температуры замкнутой системы она (система) должна быть макроскопической (состоять из большого числа «частиц»⁵) и быть равновесной.⁶ Температура является скалярным, интенсивным параметром⁷. В равновесной термодинамической системе температура должна быть постоянной по всему объему. Температура определяет внутреннюю энергию системы и с точки зрения статистической термодинамики определяет вероятность состояния системы. В соответствии со сказанным приведем следующие формулы:

- энергия идеального газа (i – число степеней свободы «частицы» идеального газа, N – число частиц).

- закон Стефана-Больцмана (плотность энергии равновесного теплового излучения).

- вероятность системы, погруженной в термостат находится в i-ом квантовом состоянии. E_i – энергия этого состояния. В этих формулах T – температура по шкале Кельвина.

2. Первый закон термодинамики (первое начало). Химический потенциал.

Первый закон термодинамики записывают в виде

Энергию системы можно изменить тремя способами. Сообщить тепло, совершить над системой работу и добавить число частиц.⁸ В третье слагаемое входит величина , называемая химическим потенциалом. В соответствии с формулой

.

Химический потенциал численно равен удельному изменению энергии в условиях отсутствия теплообмена и работы.⁹

3. Второй закон термодинамики (второе начало).

«Невозможен процесс, единственным конечным результатом которого будет превращение в работу теплоты, извлеченной из источника, имеющего всюду одинаковую температуру». (Постулат Кельвина, невозможность вечного двигателя второго рода.)

«Невозможен процесс, единственным конечным результатом которого был бы переход теплоты от тела с данной температурой к телу с более высокой температурой». (Постулат Клаузиуса.)

4. Т ермодинамическая температура (шкала).

Абсолютная термодинамическая шкала температур строится на основе циклического процесса.

Здесь показан точный график цикла Карно с условными параметрами Т₂ = 2, Т₁ = 1, R = 1. В ходе цикла на участке 2 – 3 принимается теплота Q₂ от источника при температуре Т₂, на участке 4 – 1 отдается количество теплоты Q₁ системе имеющей температуру Т₁.

Можно показать что, для равновесного цикла Карно величина отношения теплот цикла является функцией только температур и не зависит от «рабочего тела» тепловой машины.

. (1) З десь t – температура, определяемая по произвольной шкале температур. Определим вид функции . Для этого рассмотрим циклы между тремя температурами. В соответствии с формулой (1) записываем

.

Считаем, что в первом и втором циклах «теряется» одно и тоже количество теплоты Q₀. Из полученных трех отношений получаем

Эта формула будет справедливой, если функция является функцией отношения двух одинаковых функций, но с различными значениями переменных

.

Универсальную неизвестную функцию (t) (с точностью до константы) можно считать абсолютной термодинамической температурой

.

В этом случае отношение теплот цикла будет равно отношению термодинамических температур

.