Пензенский государственный педагогический университет им. В. Г. Белинского

Кафедра "Вычислительные системы и моделирование"

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СОЦИАЛЬНЫХ ПРОЦЕССОВ

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

составитель В. И. Горбаченко

2006

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

1. МЕТОД ЭЙЛЕРА РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ 4

1.1. Постановка задачи. Пример логистического уравнения 4

1.2. Метод Эйлера решения ОДУ и систем ОДУ 6

1.3. Контрольные вопросы 8

1.4. Задания 8

2. РЕШЕНИЕ ЛОГИСТИЧЕСКОГО УРАВНЕНИЯ С ПОМОЩЬЮ ЭЛЕКТРОННЫХ ТАБЛИЦ EXCEL 10

2.1. Цель работы 10

2.2. Постановка задачи 10

2.3. Решение дифференциального уравнения с помощью электронных таблиц Excel 10

2.4. Построение графика решения 11

2.5. Исследование решения 12

2.5. Контрольные вопросы 14

2.6. Задания 14

3. ИССЛЕДОВАНИЕ МОДЕЛИ ЛОТКИ‑ВОЛЬТЕРРЫ 15

3.1. Цель работы 15

3.2. Постановка задачи 15

3.3. Решение системы дифференциальных уравнений с помощью электронных таблиц Excel 16

3.4. Контрольные вопросы 18

3.5. Задания 18

4. ИССЛЕДОВАНИЕ МОДЕЛЕЙ ДИНАМИЧЕСКОГО ХАОСА 19

4.1. Цель работы 19

4.2. Постановка задачи 19

4.3. Исследование динамического хаоса с помощью электронных таблиц Excel 19

4.4. Контрольные вопросы 23

4.5. Задания 23

5. МОДЕЛИ КЛЕТОЧНЫХ АВТОМАТОВ 24

5.1. Цель работы 24

5.2. Постановка задачи 24

5.3. Построение модели 25

5.4. Проведение эксперимента 27

5.5. Контрольные вопросы 28

5.6. Задания 28

ЛИТЕРАТУРА 29

Введение

Математическая модель – это приближенное описание какого-либо класса явлений с помощью математической символики [1, 2, 3].

Можно выделить "жесткие" и "мягкие" модели [4]. Жесткие модели используются в точных науках и подразумевают построение и исследование возможно точной модели. Мягкие модели используются в экономике, социологии и других гуманитарных науках и нацелены на качественные исследования, на выявление закономерностей. Мягкие модели оперируют неточными данными и требуют многовариантных исследований при различных исходных данных и параметрах модели.

Данный лабораторный практикум использует основные подходы согласно учебному пособию [5]. В качестве аппарата исследования применяются, в основном, простейшие численные методы, а в качестве программного обеспечения – электронные таблицы Excel. Это позволяет студенту при минимальных знаниях математики и информатики проводить реальные исследования.

1. Метод эйлера решения обыкновенных дифференциальных уравнений и систем уравнений

1.1. Постановка задачи. Пример логистического уравнения

Обыкновенное дифференциальное уравнение (ОДУ) первого порядка имеет вид

, где – независимая переменная (очень часто – это время), – искомая функция.

Уравнение решается при начальных условиях

.

ОДУ второго порядка имеет вид

с начальными условиями

.

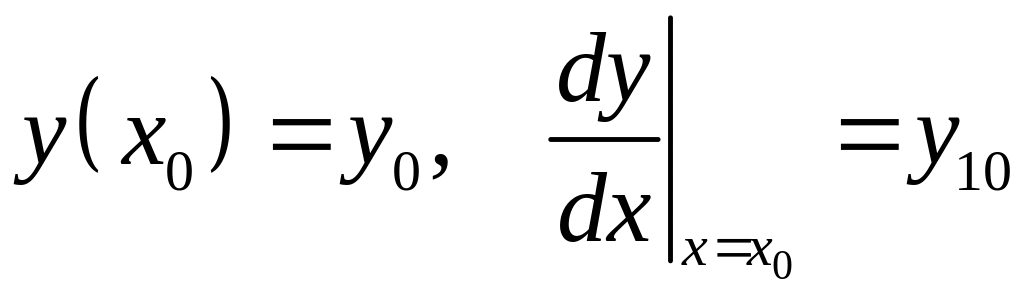Аналогично можно записать ОДУ более высоких порядков.

Система из ОДУ записывается в виде

где – решение системы, – независимая переменная.

Начальные условия имеют вид

.

Многие природные и социальные процессы описываются так называемым логистическим уравнением. В 1798 г. английский экономист Т. Мальтус предложил модель неограниченного роста численности биологической популяции. Модель Мальтуса описывается ОДУ

с начальным условием: при .

В уравнении приняты обозначения: – число óсобей популяции, – скорость рождения, – время. Уравнение означает, что скорость изменения числа особей популяции пропорциональна численности популяции .

Решение уравнения имеет вид: , что означает неограниченный рост популяции. Очевидно, что численность популяции ограничена с учетом смертности и ограниченных ресурсов среды обитания (емкости экологической ниши). Более точно процесс изменения численности популяции описывается логистическим уравнением

с начальным условием: при , где – емкость экологической ниши (сколько особей могут жить на данной территории), – скорость смертности.

Решение уравнения описывается логистической кривой [1]

Решение стремится к стационарному состоянию

,

которое получается, если в .

На рис. 1.1 представлен график логистической кривой , полученный при . В этом случае стационарное состояние равно , т. е. график представляет решение при .

Рис. 1.1. График логистической кривой при

Из графика видно, сначала популяция растет достаточно медленно, затем наблюдается рост, близкий к линейному, затем рост замедляется и решение стремится к стационарному состоянию. График логистической кривой при представлен на рис. 1.2.

Рис. 1.2. График логистической кривой при

Нами рассмотрена модель изолированной, не взаимодействующей с другими видами популяции. Реально в природе виды конкурируют друг с другом за кормовые ресурсы и жизненное пространство, охотятся друг на друга.