Термодинамика квантовых систем. Излучение абсолютно черного тела. Закон Стефана-Больцмана.
Рассмотрим некоторый объем заполненный равновесным тепловым излучением при температуре T. Стоячие тепловые волны можно рассматривать как квантовые гармонические осцилляторы. Будем считать отдельный квантовый осциллятор термодинамической системой погруженной в термостат. Запишем статистическую сумму такой системы.
.
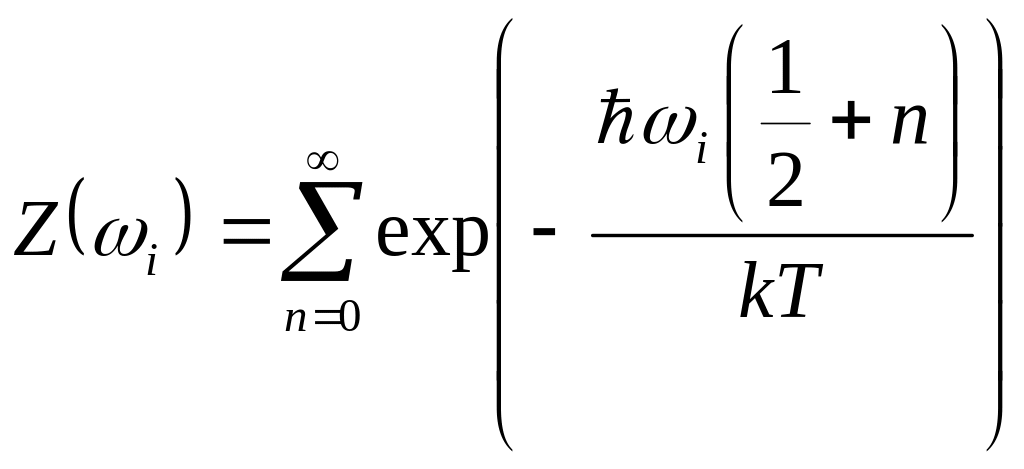(96)
Здесь мы использовали формулу
квантования энергии осциллятора
.
(97)
Статистическая сумма (96) легко
вычисляется.
.
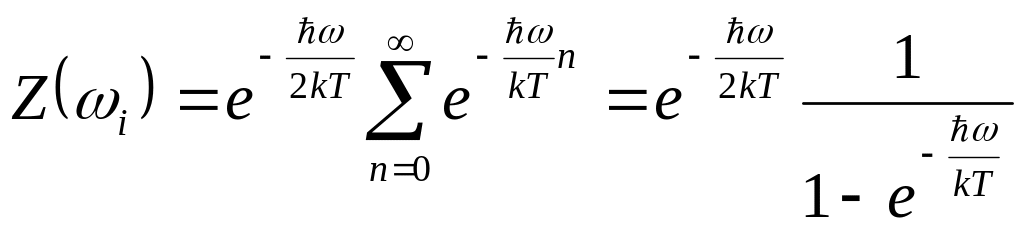(98)
Определим среднюю энергию
осциллятора в термостате.
.
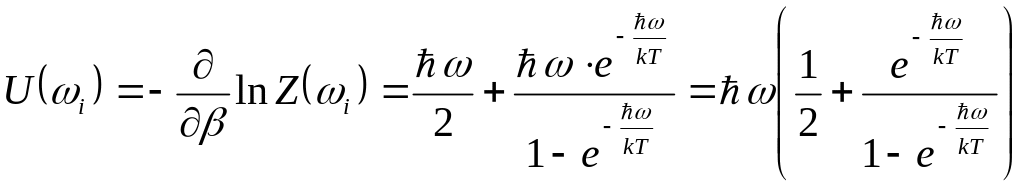
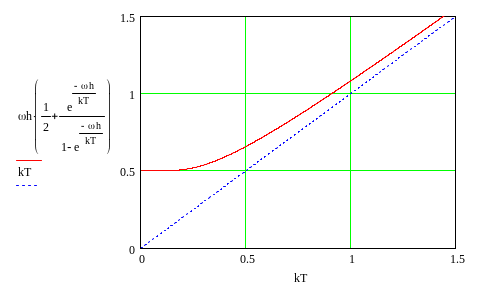(99)
При абсолютном нуле энергия
осциллятора равна
.
При высоких температурах энергия
становится классической
.
На две степени свободы по kT/2.
Полная энергия теплового излучения
записывается как сумма энергий всех
осцилляторов.
.
Заменим дискретное распределение частот непрерывным распределением, а сумму интегралом.
.
(100)
Для определения частотной функции
плотности осцилляторов воспользуемся
результатом энергетического трехмерного
квантования (для частицы в «ящике»).
.
В пространстве квантовых чисел это соотношение можно представить уравнением сферы.
.
Радиус
энергетической поверхности в пространстве
квантовых чисел.
.
«Объем» числа состояний под энергетической поверхностью
.
(100)
Число
состояний на поверхности сферы в слое
dE
.
Перейдем в импульсное пространство, используя квазиклассическое приближение.
.
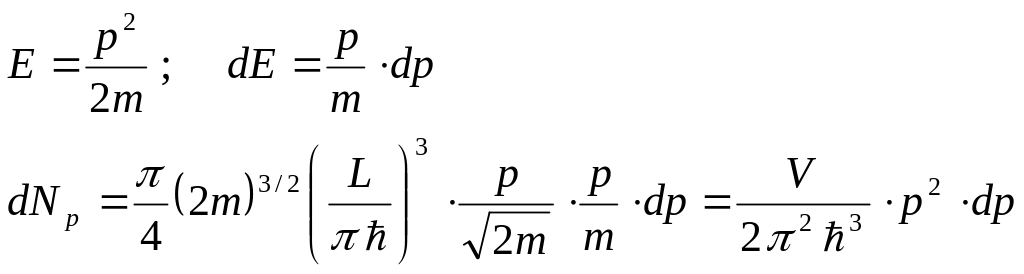Теперь можно перейти к «фотонам» и частотам.
.
.
Это число состояний следует увеличить в два раза с учетом поляризации квантов.
.
Из последней формулы получаем частотную функцию плотности числа осцилляторов
.
(101)
Используя эту формулу, записываем
интеграл энергии.
.
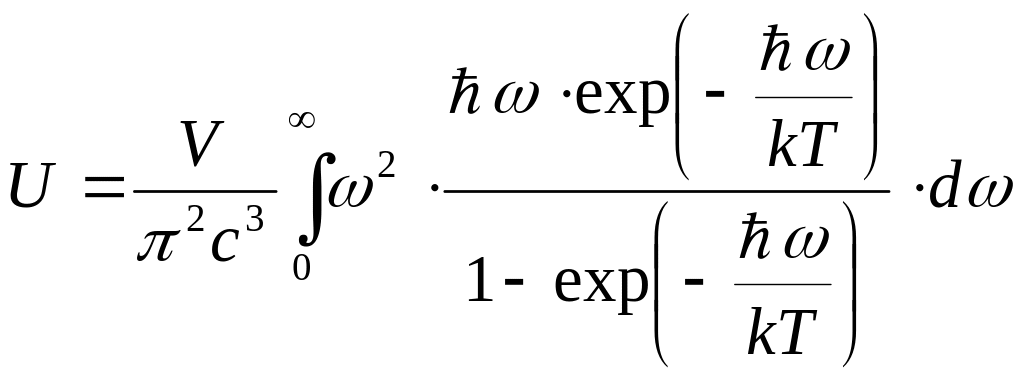При интегрировании перейдем к новой переменной
.
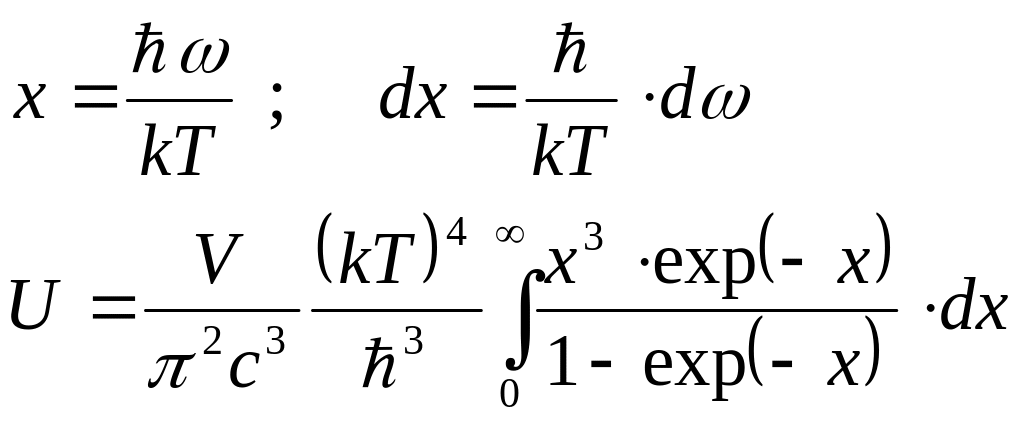Часть подынтегральной функции можно «развернуть» в ряд.
.
Вычислим один из интегралов ряда
.
В выражении плотности энергии появляется
известный ряд (приближенно равный 1,
)
.
.
(102)
Получили интегральный закон
Стефана-Больцмана. Плотность энергии
равновесного теплового излучения
пропорциональна четвертой степени
абсолютной температуры.
Используя формулу (101) и (99) можно
записать формулу Планка, которая
о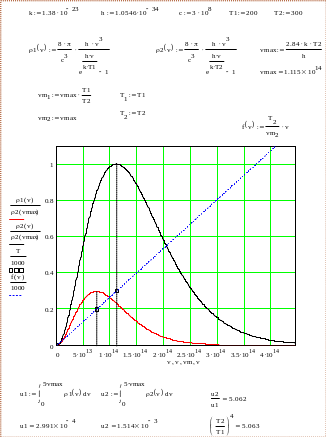
писывает
спектральную плотность энергии.
.
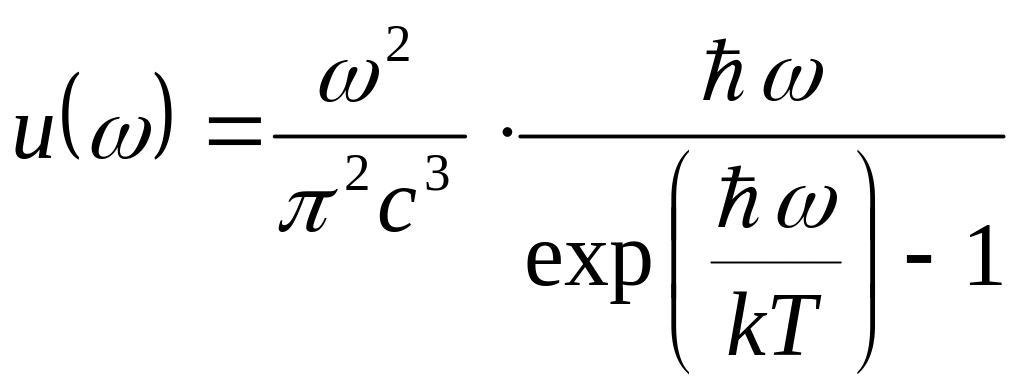(103)
Функцию можно переписать для
обычной частоты
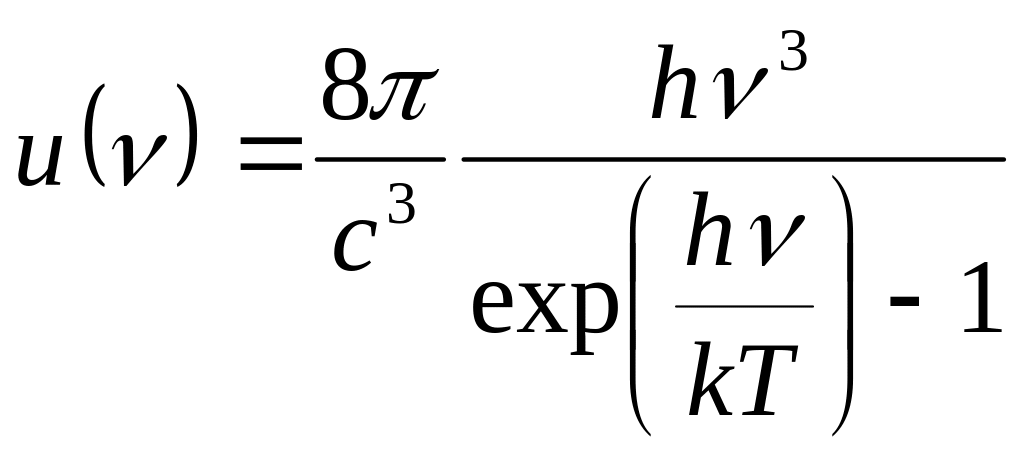(104)
Здесь представлен листинг MathCAD,
на котором построены графики спектральной
плотности для двух температур (200 и 300
К). При построении графиков функцию
плотности нормировали на максимальное
значение второго графика. Для этого
было использовано приближенное значение
частоты максимума (см. ниже). Здесь же
на общем графике показан линейный закон
Вина.
.
(105)
Частота, соответствующая максимуму распределения пропорциональна температуре. Этот закон легко получить дифференцированием функции распределения.
.
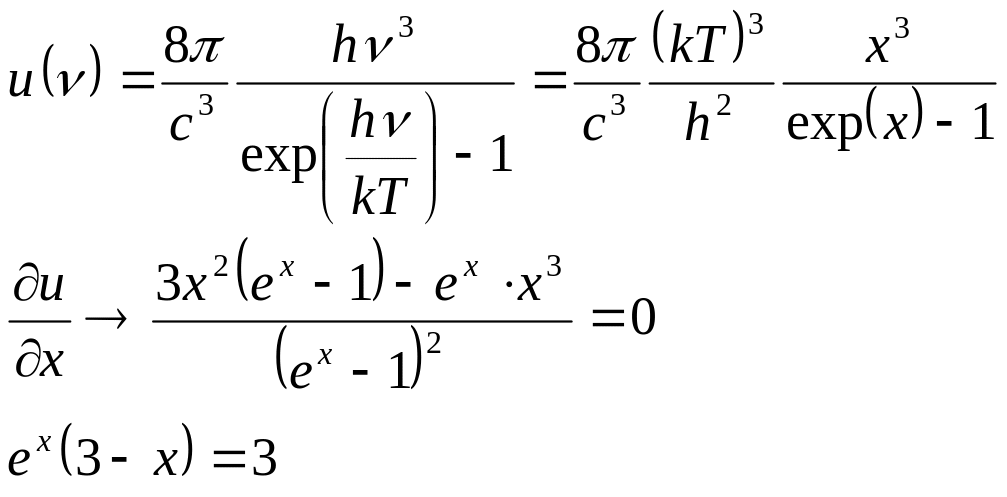П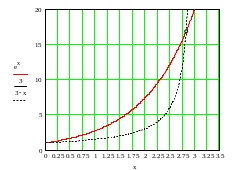
риближенное
решение трансцендентного уравнения
.
Это графическое решение, полученное в MathCAD.
.
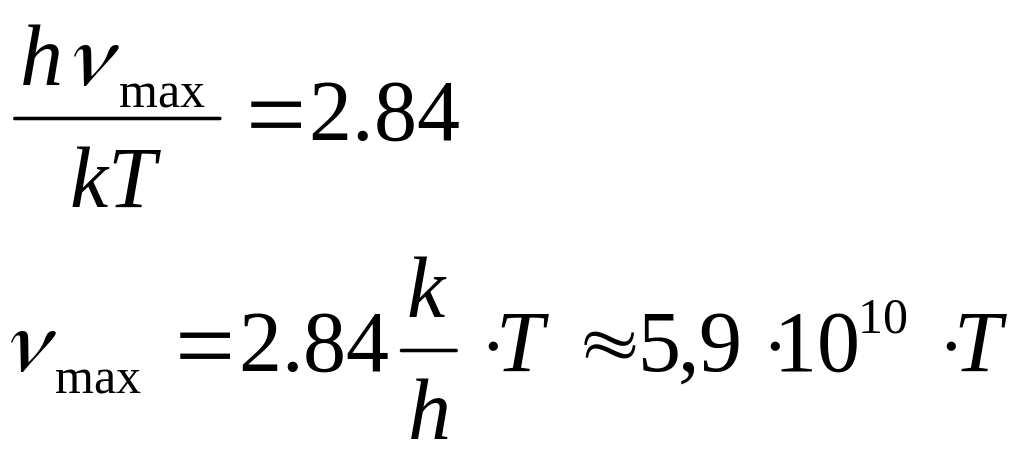(106)
Закон Вина обычно записывают
через длину волны. Для этого нужно
переписать спектральную плотность в
«волновом» виде (учитывая
).
.
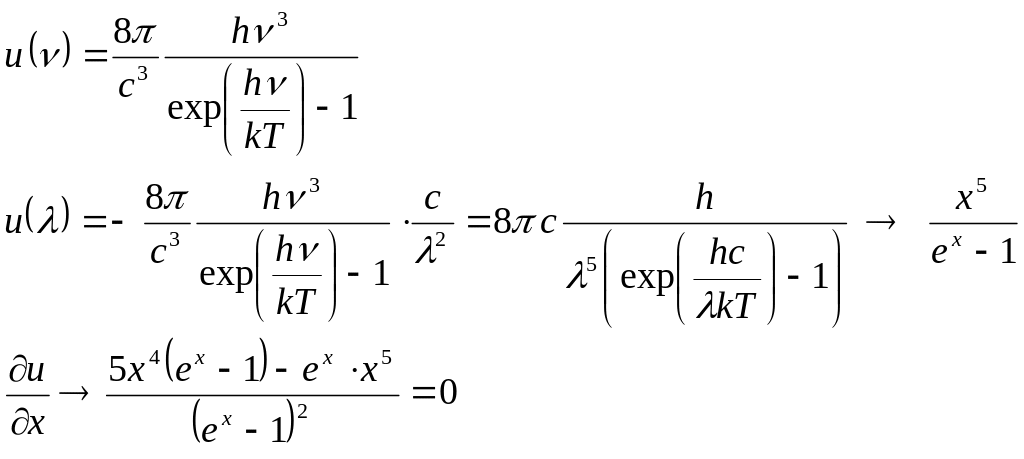Уравнение, определяющее максимум «волновой» функции плотности.
.
Приближенное решение этого уравнения
.
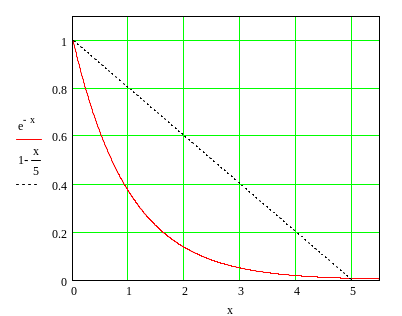
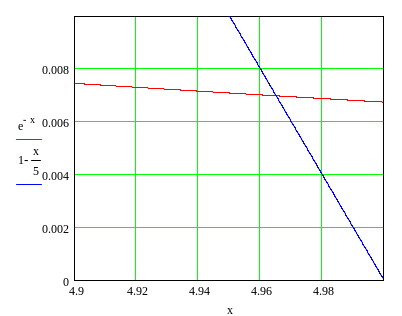
Графическое решение трансцендентного уравнения .
Закон «смещения Вина» для длины волны соответствующей максимуму функции распределения.
.
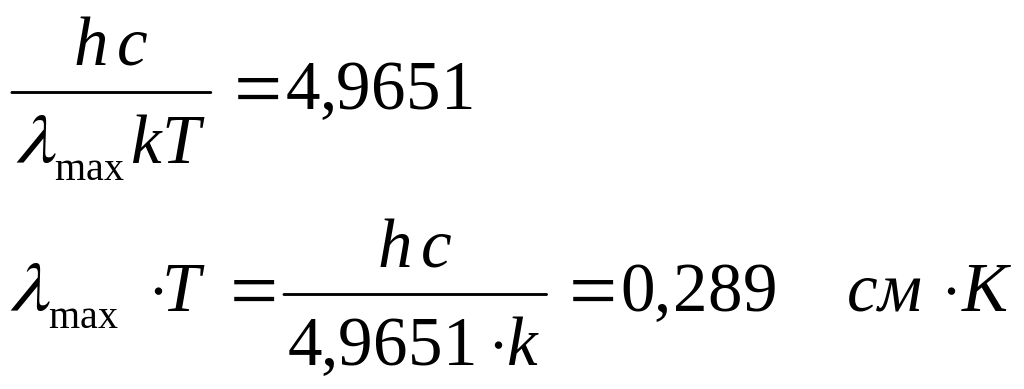(107)
Задача. Получить закон Стефана-Больцмана «термодинамическим» методом.
Используем формулу давления излучения
на поглощающую стенку
и уравнение энергии
.
Далее записываем первый закон термодинамики
.
Выделим полный дифференциал энтропии
.
Для полного дифференциала справедливо («перекрестные» производные дифференциальных множителей равны)
.
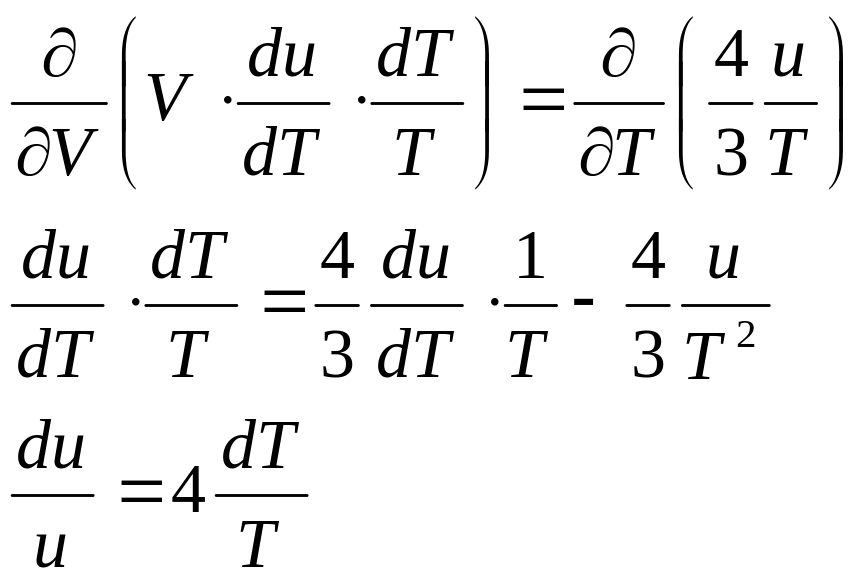Интегрируем последнее соотношение и получаем закон Стефана-Больцмана.
.