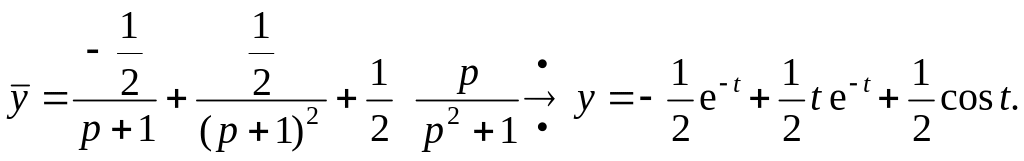- •Введение
- •Программа
- •1. Ряды
- •1.1. Сходимость числовых рядов
- •1.2. Степенные ряды. Разложение функций в степенные ряды
- •1.3. Применение степенных рядов
- •1.4. Ряды Фурье и их применение
- •2. Дифференциальное исчисление функций нескольких переменных
- •2.1. Частные производные и дифференциалы функций нескольких переменных
- •2.2. Экстремум функций нескольких переменных
- •2.3. Оптимизация функций нескольких переменных
- •3. Интегральное исчисление функций нескольких переменных
- •3.1. Двойной интеграл. Замена переменных
- •3.2. Вычисление объемов тел с помощью двойного интеграла
- •3.3. Вычисление тройного интеграла в декартовых координатах
- •3.4. Вычисление тройного интеграла в цилиндрических и сферических координатах
- •3.5. Криволинейный интеграл первого рода
- •3.6. Криволинейный интеграл второго рода
- •3.7. Теорема Грина и независимость криволинейного интеграла от пути интегрирования
- •4. Элементы теории поля
- •4.1. Операционное исчисление и его применение
- •Контрольная работа 6
- •Контрольная работа 7
- •Контрольная работа 8
- •5. Теория вероятностей
- •5.1. Основные понятия теории вероятностей
- •5.2. Повторение независимых опытов
- •5.3. Случайные величины и их числовые характеристики
- •5.4. Система двух случайных величин и регрессия
- •6. Основы математической статистики
- •Контрольная работа 9
- •Контрольная работа 10
- •Рекомендательный библиографический список
- •Оглавление
4. Элементы теории поля
4.1. Операционное исчисление и его применение
Поля физических величин (температуры, сил, скоростей и т.п.) задаются скалярными и векторными функциями нескольких переменных. Скалярные поля и их характеристики (градиент, производная по направлению и т.д.) изучены ранее. Для векторного поля, задаваемого векторной функцией точки
![]() ,
,
основными характеристиками являются:
силовые (векторные) линии или линии тока с уравнениями:
![]() ;
;
ротор или вихрь, определяющий меру и направление «завихренности» силовых линий,
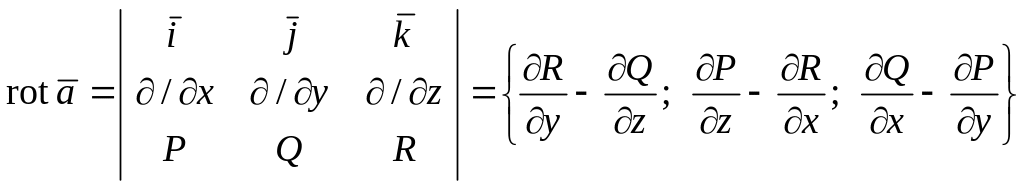 ;
(35)
;
(35)
дивергенция или расходимость, определяющая наличие источников,
![]() ;
(36)
;
(36)
поток векторного поля через
поверхность с
единичной нормалью
![]() ,
который вычисляется как поверхностный
интеграл второго рода
,
который вычисляется как поверхностный
интеграл второго рода
![]() ,
(37)
,
(37)
где
![]() – уравнение поверхности ;
S – проекция
на плоскость xOy , знак плюс
(соответственно, минус) берется, если
угол между нормалью
и осью Oz – острый (тупой);
– уравнение поверхности ;
S – проекция
на плоскость xOy , знак плюс
(соответственно, минус) берется, если
угол между нормалью
и осью Oz – острый (тупой);
циркуляция векторного поля по замкнутому ориентированному контуру определяется как криволинейный интеграл второго рода:
![]() .
(38)
.
(38)
Для замкнутой поверхности с внешней нормалью , ограничивающей объем V, справедлива теорема Гаусса – Остроградского:
![]() .
.
Для замкнутого контура , ограничивающего поверхность с нормалью , направление которой согласовано с направлением обхода контура (из конца нормали обход виден против часовой стрелки) справедлива теорема Стокса:
![]() .
.
Если векторное поле
не имеет источников и стоков
![]() ,
то поле называется соленоидальным.
Если поле имеет потенциал w,
т.е.
,
то поле называется соленоидальным.
Если поле имеет потенциал w,
т.е.
![]() ,
то поле называется потенциальным.
В таком поле работа А
(криволинейный интеграл второго рода)
не зависит от пути и по формуле (27) равна
разности потенциалов:
,
то поле называется потенциальным.
В таком поле работа А
(криволинейный интеграл второго рода)
не зависит от пути и по формуле (27) равна
разности потенциалов:
![]() .
.
Условие потенциальности поля в односвязной области пространства состоит в равенстве нулю ротора, а его потенциал находится по формуле:
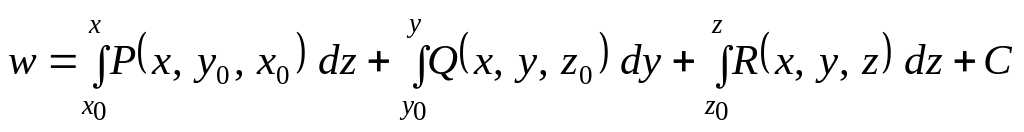 ,
(39)
,
(39)
где![]() – произвольная фиксированная точка
области.
– произвольная фиксированная точка
области.

![]() через замкнутую поверхность ,
образованную параболоидом
через замкнутую поверхность ,
образованную параболоидом
![]() и плоскостью z = 1 (нормаль –
внешняя). Вычислить циркуляцию (двумя
способами) по контуру пересечения этих
поверхностей (обход осуществляется
против часовой стрелки). Проверить,
является ли поле соленоидальным или
потенциальным (в случае
потенциальности найти потенциал).
и плоскостью z = 1 (нормаль –
внешняя). Вычислить циркуляцию (двумя
способами) по контуру пересечения этих
поверхностей (обход осуществляется
против часовой стрелки). Проверить,
является ли поле соленоидальным или
потенциальным (в случае
потенциальности найти потенциал).
Решение. Поверхность
состоит из частей
![]() и
и
![]() .
Проекции на плоскость xOy поверхностей
.
Проекции на плоскость xOy поверхностей
![]() и
и
![]() (рис.18) совпадают с проекцией объема V,
заключенного внутри поверхности .
Граница этой проекции есть единичная
окружность:
(рис.18) совпадают с проекцией объема V,
заключенного внутри поверхности .
Граница этой проекции есть единичная
окружность:
![]() ,
т.е.
,
т.е.
![]() – единичный круг.
– единичный круг.
Внешняя нормаль
![]() поверхности
образует острый угол с осью Оz
(рис.18), поэтому поток поля
поверхности
образует острый угол с осью Оz
(рис.18), поэтому поток поля
![]() по (37)
по (37)
![]() .
.
Внешняя нормаль
![]() поверхности
образует тупой угол с осью Oz (рис.18),
поэтому поток поля
по (37)
поверхности
образует тупой угол с осью Oz (рис.18),
поэтому поток поля
по (37)
![]() .
.
Переходя к полярным координатам, получим
![]() .
.
Полный поток поля П через поверхность равен сумме потоков П1 через 1 и П2 через 2:
![]() .
.
По теореме Гаусса – Остроградского полный поток
![]()
![]() .
.
Контур, образованный пересечением
поверхностей
![]() и
,
является единичной окружностью
и
,
является единичной окружностью
![]() ,
,
![]() ,
,
![]() (рис.18). По формуле (38) циркуляция по этому
контуру
(рис.18). По формуле (38) циркуляция по этому
контуру
![]()
![]()
С другой стороны, по формуле (35) ротор
поля
![]()
![]()
и по теореме Стокса для поверхности
![]() имеем
имеем
![]() .
.
Так как
![]() ,
то поле потенциально во всем пространстве.
Найдем потенциал по формуле (39), где
,
то поле потенциально во всем пространстве.
Найдем потенциал по формуле (39), где
![]() ,
,
![]() .
.
Так как по (36)
![]() ,
то поле несоленоидально.
,
то поле несоленоидально.
Пусть непрерывная функция
![]() определена при
(при
определена при
(при
![]() считаем
считаем
![]() ).
Преобразование Лапласа сопоставляет
функции
,
т.е. оригиналу, его изображение:
).
Преобразование Лапласа сопоставляет
функции
,
т.е. оригиналу, его изображение:
![]() или
или
![]()
где p = u + iv –
комплексный параметр. Несобственный
интеграл сходится,
если
![]() и
и
![]() (изображение для оригинала существует).
Преобразование Лапласа линейно, т.е.
(изображение для оригинала существует).
Преобразование Лапласа линейно, т.е.
![]() ,
где = const.
Если
,
где = const.
Если
![]() и
и
![]() ,
то преобразование Лапласа обладает
следующими свойствами:
,
то преобразование Лапласа обладает
следующими свойствами:
1) ![]() ,
где
,
где
![]() (теорема подобия);
(теорема подобия);
2) ![]() ,
где
,
где
![]() (теорема смещения);
(теорема смещения);
3) ![]() ,
где
,
где
![]() при
при
![]() (теорема запаздывания);
(теорема запаздывания);
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() (теорема о свертке).
(теорема о свертке).
Приведем таблицу изображений (табл.2) основных элементарных функций (при t < 0 все оригиналы считаются равными нулю):
Таблица 2
Оригинал |
Изображение |
Оригинал |
Изображение |
1 |
1/р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 32.
Найти изображения и оригиналы для
следующих функций: 1) ![]() 2)
2) ![]() ;
3)
;
3) ![]() .
.
Решение. 1. Так как по табл.2
![]() ,
то по теореме смещения
,
то по теореме смещения
![]() .
.
2. По табл.2
![]() и по еt
имеем
и по еt
имеем
![]()
3. Выделяя полный квадрат в знаменателе и смещение в числителе, имеем
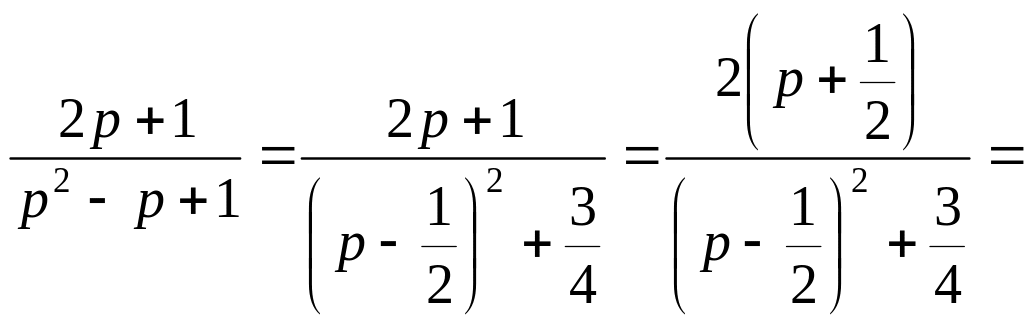
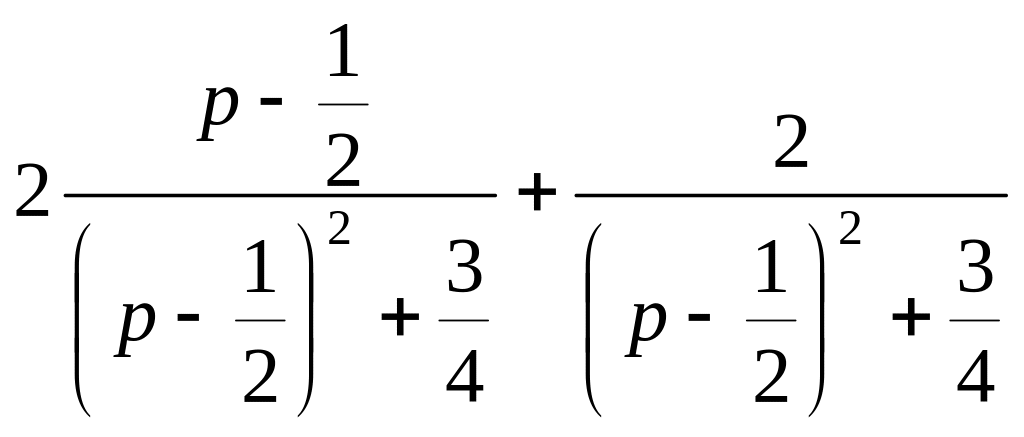 .
.
По теореме смещения и табл.2, получим
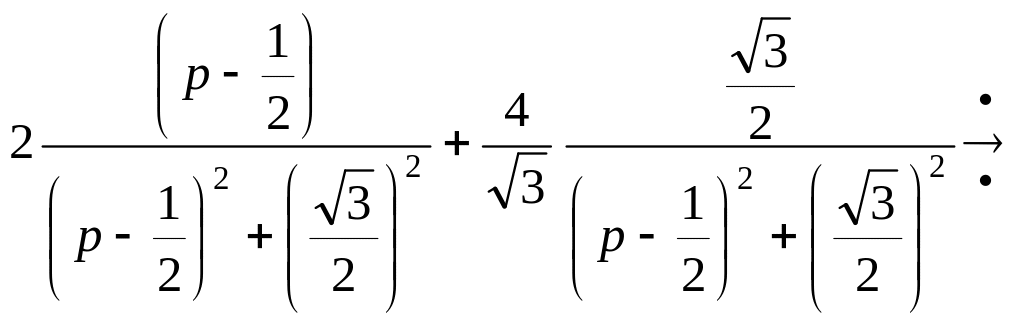
![]() .
.
Используя четвертое свойство, дифференциальные уравнения для оригиналов можно переводить в алгебраические для изображений, решить которые значительно проще.
Пример 33. Решить уравнение
![]()
Решение. Пусть
![]() .
Тогда
.
Тогда
![]()
![]() .
.
Переходя к изображениям в уравнении, имеем
![]() .
.
Для возвращения к оригиналам используем разложение на простейшие дроби:
![]()
![]()
![]() .
.
При
![]() получим
получим
![]() .
.
По методу неопределенных коэффициентов имеем
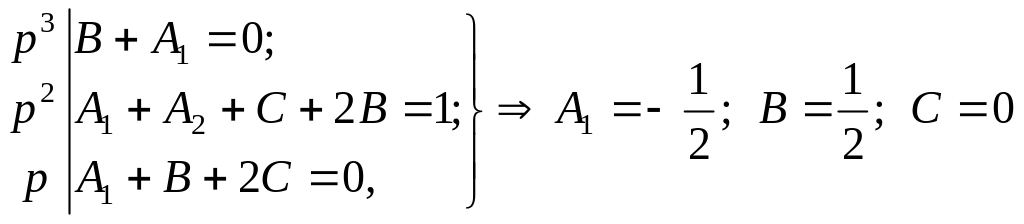 .
.
Следовательно, возвращаясь к оригиналам, получим решение