2.2. Экстремум функций нескольких переменных

Точки, в которых все частные производные функции обращаются в нуль или не существуют, являются подозрительными на экстремум (необходимое условие экстремума). Достаточные условия экстремума формулируются для функций любого числа переменных, но мы рассмотрим только случай функции двух переменных : если в стационарной точке M (где все частные производные первого порядка равны нулю) найдены значения вторых частных производных

, то

1) если дискриминант , то в точке M есть экстремум, причем максимум при A < 0 и минимум при A > 0;

2) если , то в точке M нет экстремума;

3) если , то необходимо дополнительное исследование.

Пример 10. Найти экстремум функции .

Решение. Находим стационарные точки:

Найдем решения первого уравнения и подставим их во второе:

;

.

Таким образом, стационарными точками являются точки:

Определим вторые частные производные:

;

;

.

Для первой и второй стационарных точек и соответственно имеем

;

;

.

Так как , то экстремума нет.

Для третьей и четвертой стационарных точек и соответственно имеем

;

;

;

.

Так как , то в точках M₃ и M₄ есть экстремум, причем и .

2.3. Оптимизация функций нескольких переменных

Для отыскания наибольшего или наименьшего значения функций нескольких переменных в ограниченной замкнутой области достаточно найти значения этой функции в подозрительных на экстремум точках внутри области и сравнить с ее наибольшим и наименьшим значениями на границе области.

Пример 11. Найти наибольшее и наименьшее значения функции в области и .

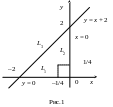
Решение. Область ограничена линиями х = –2, х = 0, и представляет собой треугольник, ограниченный тремя линиями L₁, L₂ и L₃ (рис.1).

Найдем стационарные точки:

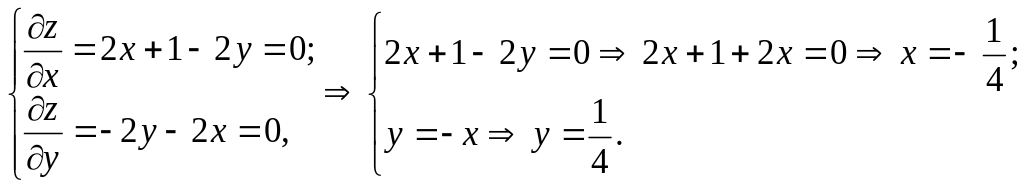
Точка (–1/4,1/4) лежит внутри области .

Исследуем функцию на наибольшее и наименьшее значения на границе области. Уравнение линии L₁ есть y = 0, где –2  х  0 и на L₁ функция z – функция только переменной x, заданная на отрезке [–2, 0]:

.

Производная при и .

Значения функции z₁ на концах отрезка [–2, 0]: .

Уравнение линии L₂ есть где 0  y  2, и на L₂ функция z – функция только переменной y, заданная на отрезке [0, 2]:

.

Производная при . Значения функции z₂ на концах этого отрезка: z₂(0) = z₁(0); z₂(2) = –4.

Уравнение линии L₃ есть где –2 £ х £ 0, и на L₃ функция – функция только переменной x, заданная на отрезке [0, 2]:

Производная при , и . Значения функции z₃ на концах этого отрезка: .

Сравнив значения функции во всех найденных точках, определим наибольшее (z^*) и наименьшее (z_*) значения функции в заданной области:

z^* =  ;

z_* =  .

Сглаживанием опытных данных, полученных в результате измерений и расчетов с некоторой погрешностью, называется отыскание конкретного вида функциональной зависимости, которой лучше всего отвечают эти данные. Простейшим методом сглаживания является метод наименьших квадратов.

По методу наименьших квадратов из некоторого класса зависимостей (a, b, c, … – параметры) выбирается та, для которой минимальна сумма квадратов всех отклонений значений функции в заданных точках (k = 1, 2, …, n) от соответствующих экспериментальных данных y_k:

.

Полученную таким образом зависимость называют эмпирической.

Простейшим классом зависимостей является класс линейных функций . Значения параметров a и b по методу наименьших квадратов определяют из системы уравнений:

(15)

где – экспериментальные или эмпирические данные.

Пример 12. Результаты измерения величин x и y заданы в виде таблицы (табл.1).

Таблица 1

x	–2	–1	0	1	2	3
y	5,6	5	4,3	4	3,6	3

Определить эмпирическую линейную зависимость между y и x методом наименьших квадратов.

Решение. Число измерений n = 6. Найдем суммы, которые являются коэффициентами системы (15):

.

Тогда система (15) имеет вид

.

Поэтому – искомая эмпирическая линейная зависимость.

В заключение отметим, что если в задаче оптимизации область незамкнутая, то следует рассматривать на границе, которая не входит в область, пределы функции со стороны области. В частности, если этот предел на всей границе равен , то наибольшего значения у функции в области нет, а наименьшее значение достигается внутри области. Если же этот предел равен , то ситуация с наименьшим и наибольшим значением будет противоположной. Кроме того, если область неограниченная, то следует еще найти предел функции на бесконечности.