3.7. Теорема Грина и независимость криволинейного интеграла от пути интегрирования

Путь, начальная и конечная точка которого совпадают, называется замкнутым путем или контуром. Ориентированные границы плоских областей являются контурами. Области, ограниченные одним контуром, называются односвязными, а несколькими контурами – многосвязными. Направление обхода границы L области S называется положительным , если при обходе область остается слева. Для ограниченных односвязных областей это направление против часовой стрелки.

Теорема Грина. Если функции P(x, y), Q(x, y) и их частные производные непрерывны в области S с кусочно-гладкой границей L, то справедлива формула

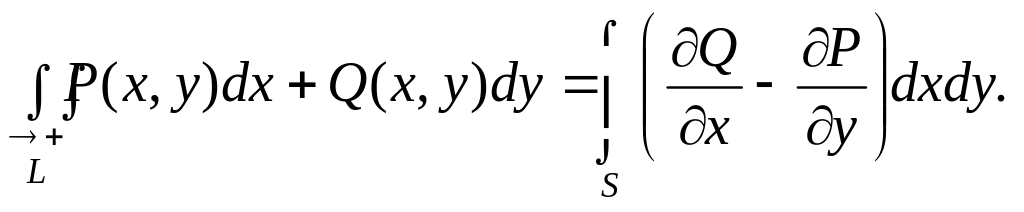(30)

Следствие. Если Q = x и P = 0 или P = y и Q = 0, то и по (30) площадь области

(31)

Пример 27. Найти площадь, ограниченную эллипсом x = acost, y = bsint.

Решение. При возрастании параметра t от 0 до 2 обход эллипса совершается в положительном направлении (см. пример 25) и поэтому по (31) имеем

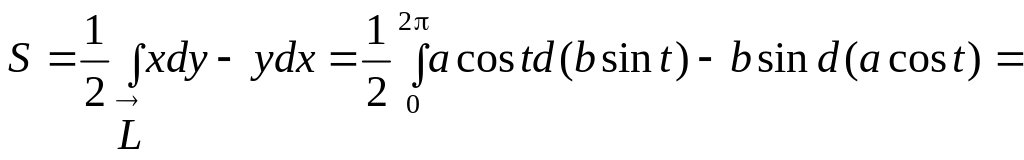
Пример 28. Найти по окружности , ориентированной по часовой стрелке.

Решение. Направление обхода окружности по часовой стрелке будет отрицательным и поэтому в (30) следует изменить знак:

Криволинейный интеграл не зависит от пути интегрирования, а зависит только от конечной и начальной точек пути в односвязной области, тогда и только тогда, когда выражение , стоящее под знаком интеграла, является полным дифференциалом некоторой функции , т.е. , и поэтому

(32)

В односвязной области условием независимости криволинейного интеграла от пути интегрирования и условием того, что подынтегральное выражение является полным дифференциалом, будет равенство частных производных . Функция , называемая потенциалом векторного поля, может быть найдена по формуле

. (33)

Пример 29. Найти непосредственно и с помощью потенциала интеграл .

Решение. Прямая делит плоскость на две односвязные области.

Обе точки и находятся в области . Вычислим в этой области частные производные:

; .

Так как производные равны между собой, то криволинейный интеграл не зависит от пути интегрирования. Выберем путь, изображенный на рис.17.

На и , на и . По формуле (28), подставляя уравнения путей, получим

.

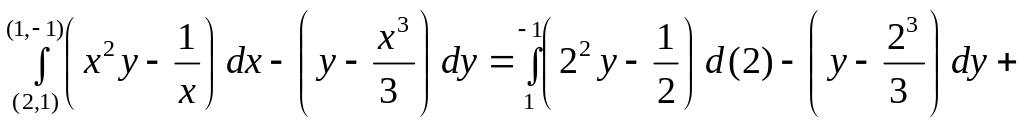
Для вычисления с помощью потенциала выберем произвольную точку области, например, (1, 0). По формулам (32) и (33) имеем

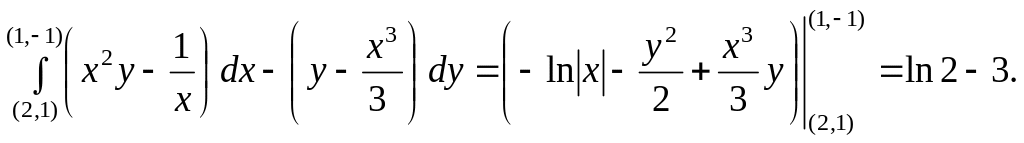
Дифференциальное уравнение первого порядка + + P(x, y) = 0 или P(x, y)dx + Q(x, y)dy = 0 является уравнением в полных дифференциалах в односвязной области, если в этой области выполнено условие .

Для такого уравнения dW = P(x, y)dx + Q(x, y)dу = 0 и

W(x, y) = C (34)

есть общее решение этого дифференциального уравнения, где функция W(x, y) является потенциалом, восстановленным по формуле (33).

Пример 30. Решить уравнение

Решение. Это уравнение не относится к изученным ранее типам. Проверим, будет ли оно уравнением в полных дифференциалах на всей плоскости xOy. Перепишем уравнение в виде . Тогда Отсюда и . найдем потенциал по формуле (33), выбрав точку (x₀, y₀) = (0, 0). Точка (0, 0) принадлежит области определения P(x, y) и Q(x, y) и их частных производных. Тогда

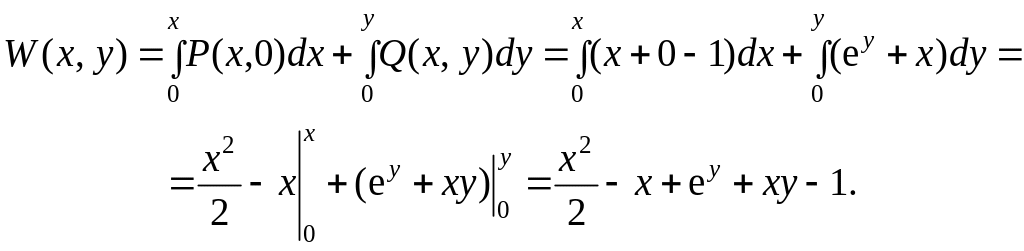
Следовательно, в соответствии с формулой (34) общее решение уравнения имеет вид

.