3.5. Криволинейный интеграл первого рода

Пусть  непрерывная функция, заданная на гладкой кривой L. Разобьем кривую L на n элементов. Введем обозначения: l_k  длина k-го элемента;  его произвольная точка.

Криволинейным интегралом первого рода называется конечный предел интегральной суммы

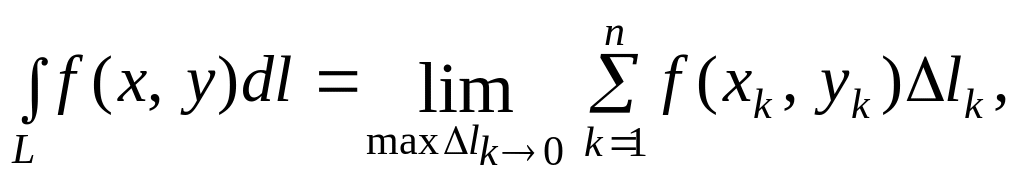
который не зависит от способа разбиения и выбора точек.

Из определения криволинейного интеграла следует формула для вычисления длины кривой:

.

Если функция двух переменных определена на дуге кривой , заданной параметрическими уравнениями и , где , то , элемент дуги и криволинейный интеграл вычисляются по формуле

. (24)

В частности, если кривая задана явно: , где , то

. (25)

В пространстве для функции трех переменных на дуге  линии, заданной параметрическими уравнениями: , и , где , аналогично имеем

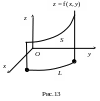
С геометрической точки зрения криволинейный интеграл , где L – кривая в плоскости xOy и , определяет площадь цилиндрической поверхности (рис.13), образующая которой параллельна оси Оz, и которая ограничена снизу дугой L, а сверху графиком функции . Для материальной дуги L c линейной плотностью справедливы следующие формулы для вычисления массы, координат центра тяжести и моментов инерции:

; ; ; ₍₂₆₎

; .

Аналогичные формулы справедливы и для пространства. Если плотность не задана, то считаем (однородная дуга).

Пример 22. Найти , если L – отрезок прямой между точками А(0, 2) и В(4, 0).

Решение. Уравнение отрезка L прямой имеет вид

Так как , то и по формуле (25) имеем

Пример 23. Найти координаты центра тяжести арки циклоиды.

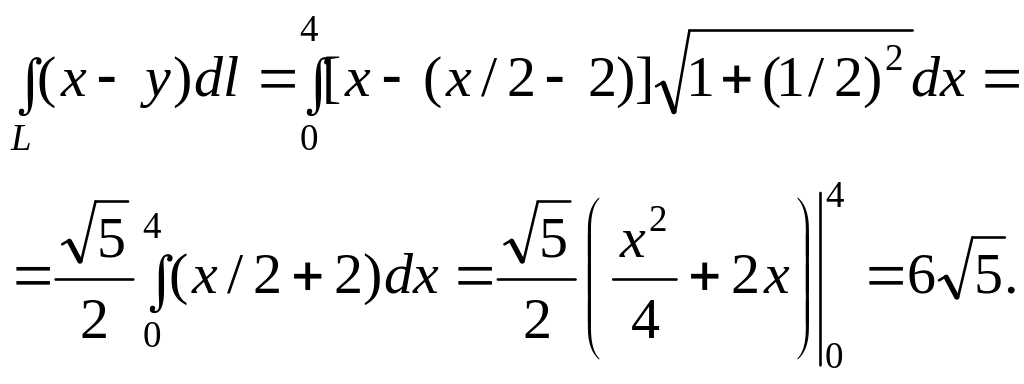
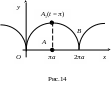
Решение. Плотность не задана, и поэтому считаем , т.е. находим геометрический центр тяжести. Арка циклоиды L , которая задается параметрическими уравнениями и , где (рис.14), симметрична относительно оси  , и поэтому центр тяжести , т.е. . Так как и , то по (24) и (26) имеем

3.6. Криволинейный интеграл второго рода

Пусть векторная функция двух переменных определена в некоторой области, содержащей ориентированную дугу линии  , заданную параметрически и , где начальной точке дуги L соответствует , конечной точке – , а вектор . Тогда криволинейный интеграл второго рода от скалярного произведения вычисляется следующим образом:

(27)

В частности, если кривая задана явным образом , где , то формула (22) преобразуется к виду

(28)

В пространстве для векторной функции трех переменных на ориентированной дуге линии  , заданной параметрически , и , где обход соответствует изменению параметра от до , аналогично имеем

(29)

С физической точки зрения криволинейный интеграл второго рода представляет собой работу переменной силы при движении материальной точки по траектории .

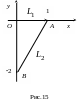
Пример 24. Найти по ломаной , где А(1, 0) и В(0, –2).

Решение. Ориентированная дуга, или путь, состоит из двух частей: и , т.е. (рис.15). Уравнение кривой L₁ y = 0, где 0  х  1, обход совершается от точки О(0, 0) к А(1, 0). Уравнение кривой L₂ имеет вид y = 2х – 2, где 1  х  0, обход от точки А(1, 0) к В(0, –2). Следовательно, используя свойство аддитивности и формулу (28), получим

Пример 25. Найти работу силового поля при движении точки в положительном направлении по части эллипса, лежащей в I квадранте.

Решение. Удобно использовать параметрическое задание эллипса , . Траектория, или путь движения, – часть эллипса от точки до , где точкам и соответствуют и (рис.16). Так как , то , и поэтому по формуле (27)

Пример 26. Найти , если и точка перемещается по первому витку винтовой линии в направлении увеличения параметра.

Решение. Первому витку винтовой линии соответствует изменение параметра t от 0 до 2. Так как , то и по формуле (29) получим