3. Интегральное исчисление функций нескольких переменных

3.1. Двойной интеграл. Замена переменных

Пусть непрерывная функция задана в ограниченной замкнутой области S плоскости xOy. Разобьем область S на n элементарных областей , введя обозначения: – площадь элементарной области; – ее диаметр (наибольшее расстояние между точками) и – ее произвольная точка .

Двойным интегралом называется предел интегральной суммы

,

если он существует, конечен и не зависит ни от способа разбиения области S на элементы, ни от способа выбора точек . В силу произвольности разбиения площадь .

Из определения двойного интеграла следует формула вычисления площади области:

.

Вычисление двойного интеграла сводится к повторному интегрированию, а его свойства и условия существования аналогичны свойствам определенного интеграла.

Пусть pr_xS и pr_yS – проекции области S на координатные оси Ox и Oy . Область S называется областью I типа или правильной в на­правлении оси Oy (S  I), если она задана системой неравенств , где [a, b] = pr_xS (рис.2). В этом случае линии с уравнениями и являются соответственно нижней и верхней границами для области S, если смотреть в направлении оси Oy (на рис.2 показано стрелкой). Если S область I типа, то

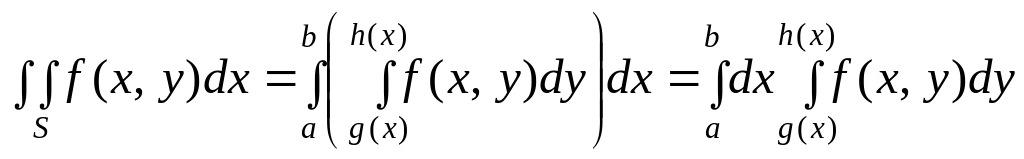. (16)

В ыражение в правой части формулы (16) называется повторным (двукратным) интегралом. Сначала вычисляется внутренний определенный интеграл по переменной y (переменная x при этом считается постоянной). Затем находят внешний интеграл по переменной x. Например,

Область S называется областью II типа, если она задается системой неравенств , где [c, d] = pr_yS (рис.3). В этом случае

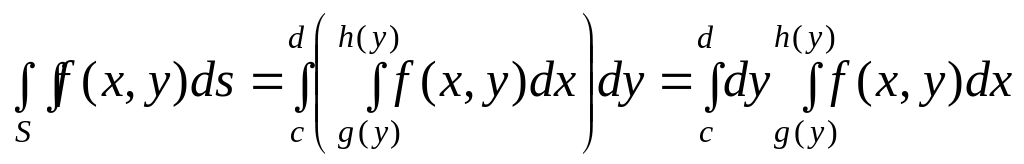. (17)

В общем случае область разбивается на области I и II типа и по свойству аддитивности двойной интеграл будет равен сумме соответствующих повторных интегралов по этим областям. Процедура сведения двойного интеграла к повторным называется расстанов­кой пределов в двойном интеграле.

Пример 13. Область S ограничена линиями y = (x – 3)², y = 0, x = 0, x = 4. Свести двойной интеграл по области к повторному двумя способами.

Решение. Первый способ. Построим область (рис.4).

Область S является областью I типа, так как она ограничена слева и справа прямыми x = 0 и x = 4, снизу – графиком функции y = 0, а сверху – графиком функции y = (x – 3)². По формуле (16) имеем

.

Второй способ. Рассматривая область как область II типа, убеждаемся, что ее граница АВС состоит из двух частей, являющихся графиками разных функций, поэтому область придется разбить на две: S₁ = OAB и S₂ = BCD. Для S₁ нижняя граница ОА задается функцией х = 0, а верхняя АВ – y = (x – 3)². Уравнения границы области II типа задаются уравнениями вида x = g(y), поэтому надо выразить x через y: , следовательно, . Знак минус соответствует левой ветви параболы (x  3), а знак плюс – правой ветви (x  3). Следовательно, по формуле (17) получим

.

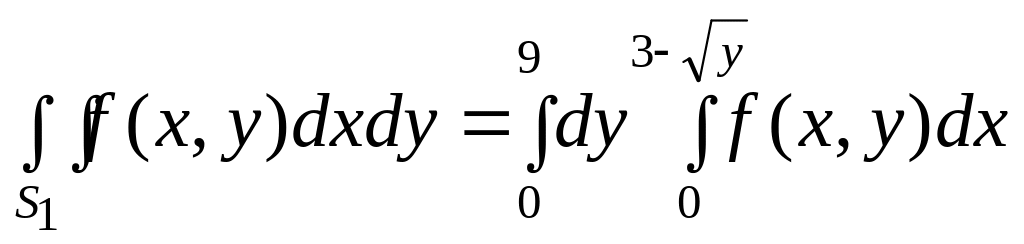Аналогично для имеем

.

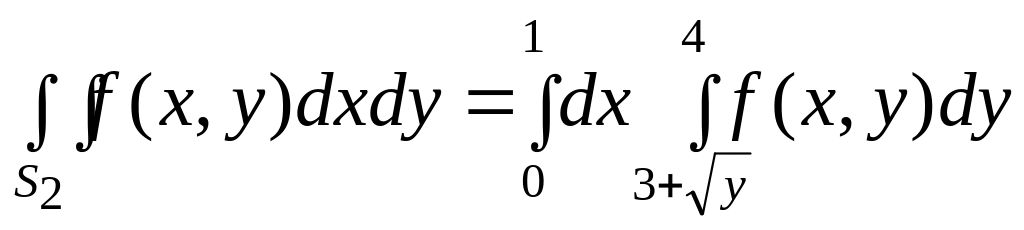Окончательно получим

Пример 14. Поменять порядок интегрирования в интеграле

.

Решение. Восстановим область интегрирования . Так как внутренней переменной является , то – область II типа. В этой области 0  y  1, . Таким образом, нижней границей является график функции x = y/2 (или y = 2х), а верхней – график функции (или y = x²). Построим эту область и найдем точки пересечения кривых и (рис.5).

Рассматривая S как область I типа, убеждаемся, что верхняя граница области состоит из двух линий и , задаваемых уравнениями y = 2х и y = 1.

Нижняя линия задается одним уравнением y = х². Разобьем область на две области и . В области имеем , , а в области имеем , . Следовательно,

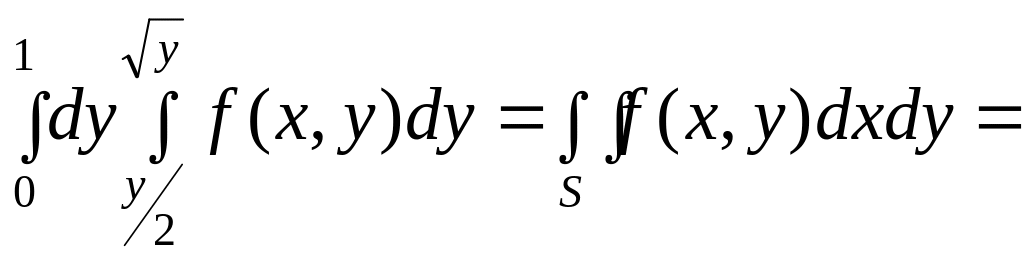
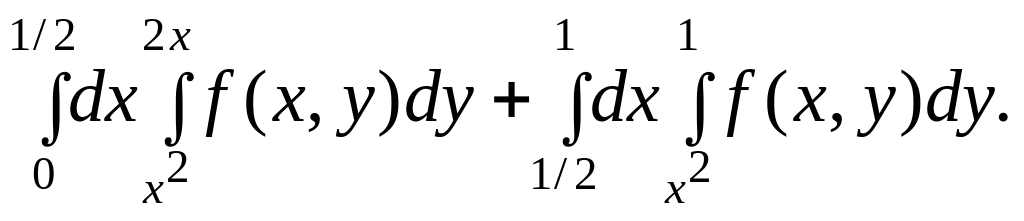
Двойной интеграл при переходе к полярным координатам ( , ) вычисляется по формуле

, (18)

где – область интегрирования в полярных координатах и коэффициент искажения элементарной области (якобиан) .

Пример 15. Найти , если – область, ограниченная кривой .

Решение. Чтобы построить область , преобразуем уравнение ее границы, выделив полный квадрат: , т.е. х²  . Это окружность радиуса 2 с центром в точке (0; 2) (рис.6).

Запишем уравнение границы в полярных координатах: , откуда . Для рассматриваемой области : , . По формуле (18) получим

.