1.4. Ряды Фурье и их применение
Функциональные ряды по тригонометрической
системе функций
на промежутке
называются тригонометрическими
рядами, или рядами Фурье.
Каждая гладкая (производная непрерывная)
или кусочно-гладкая функция f(x)
на промежутке
в точках непрерывности разлагается в
ряд Фурье
(5)
где
(6)
Если f(x) – четная функция, то
.
Если f(x) – нечетная функция, то
и
,
.
(7)
Пример 7. Разложить в ряд Фурье функцию
Эта функция не обладает симметрией и
задана на промежутке
.
Находим коэффициенты ряда Фурье по
формуле (6), причем интегралы по промежутку
возьмем по частям:
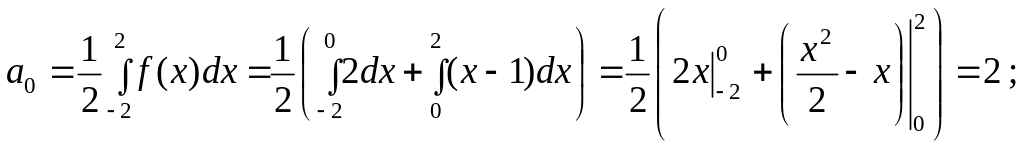
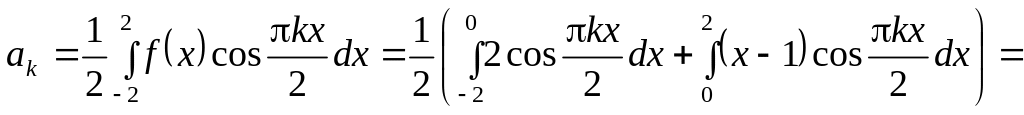
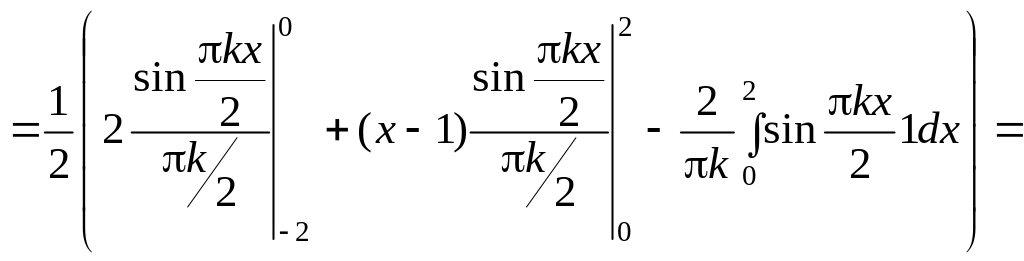
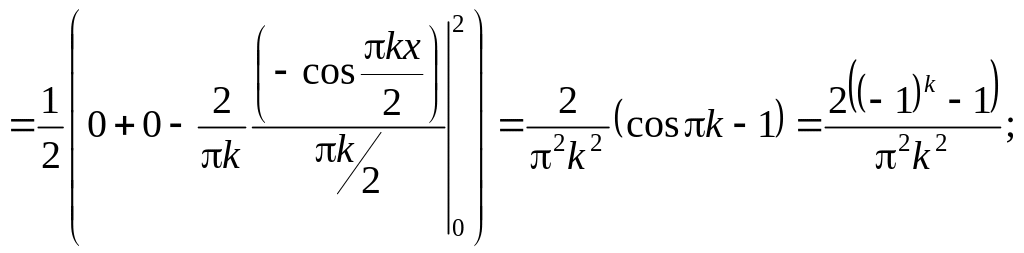
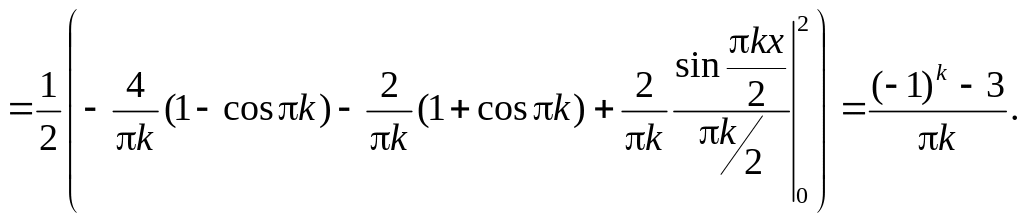
Следовательно, ряд Фурье для этой функции по (5) имеет вид
.
Ряды Фурье можно использовать для решения краевых задач математической физики. В качестве примера рассмотрим решение волнового уравнения колебаний струны с закрепленными концами. Движение струны описывается уравнением в частных производных:
,
(8)
где
– отклонение точки струны с координатой
x от положения равновесия в момент
времени t,
,
.
Граничные условия для уравнения (8) (условия закрепления концов струны):
.
(9)
Начальные условия:
,
(10)
где функции f(x) и g(x) задают начальную форму струны и начальное распределение скоростей соответственно. Это – краевая задача.
Решение поставленной задачи ищем в виде ряда Фурье по синусам для x и с коэффициентами от t (метод Фурье):
(11)
Краевые условия (9) при этом удовлетворяются
автоматически, так как
при
x = 0,l.
Подставляя (11) в уравнение (8), получим:
,
откуда
.
Решение данного уравнения имеет вид
Таким образом,
(12)
Постоянные
и
находим из начальных условий (10). Имеем
,
.
Отсюда следует, что
и
являются коэффициентами Фурье функций
f(x) и g(x)
в их представлении тригонометрическими
рядами Фурье по синусам. Поэтому по (7)
(13)
Таким образом, решением задачи является функция (12), где коэффициенты и определяются формулами (13).
Отметим, что любую функцию, заданную на
,
можно разложить в ряд Фурье по косинусам
(как четную) или по синусам (как нечетную).
2. Дифференциальное исчисление функций нескольких переменных
2.1. Частные производные и дифференциалы функций нескольких переменных
Производные функции нескольких переменных вычисляют отдельно по каждому из аргументов (остальные аргументы при этом полагают постоянными) и называют частными производными. В свою очередь, от них, как от функций нескольких переменных, можно снова находить частные производные, которые будут уже частными производными второго порядка, и т.д.
Например, для функции
имеем
;
;
;
;
;
.
Если функция
и все ее частные производные второго
порядка непрерывны, то
,
т.е. смешанные (по разным переменным)
частные производные не зависят от
порядка дифференцирования (теорема
Шварца).
Полный дифференциал – это главная часть полного приращения функции нескольких переменных, линейная относительно приращений аргументов. Полный дифференциал функции
,
где
.
Функция дифференцируема, если она имеет дифференциал. Достаточным условием этого является непрерывность частных производных первого порядка.
Применение дифференциала в приближенных
вычислениях основано на том, что он
является главной частью приращения
функции, поэтому справедливы приближенные
равенства:
и
.
(14)
Если приращения аргументов имеют смысл абсолютных погрешностей аргументов, то с помощью дифференциала можно оценить абсолютную () или относительную () погрешность вычисления функции:
;
.
Пример 8. Вычислить приближенное
значение функции
в
точке B (4,03; 1,96), исходя из ее
значения в точке A(4,2) и заменив
приращение функции дифференциалом.
Найти возникающую при этом относительную
погрешность (в процентах).
Решение. В данном случае
,
,
,
.
По (14) приближенное значение функции в точке B
.
Так как точное значение функции в точке B
,
то абсолютная и относительная погрешности равны соответственно:
0,04 %.
Формула производной сложной функции
нескольких переменных, если
и
,
имеет вид
.
Если функция одной переменной
задана неявно уравнением
,
то ее производная
,
где
,
.
Частные
производные
функции двух переменных
,
заданной неявно уравнением
,
имеют вид
,
где
.
Аналогичные выражения справедливы для производных неявно заданной функции от любого числа переменных.
Градиент функции – вектор, компонентами которого являются соответствующие частные производные
.
Градиент функции бльшего
числа переменных определяется аналогично.
Градиент в данной точке перпендикулярен
проходящей через эту точку линии
или поверхности
уровня одинаковых значений функции.
Производная функции
или
в точке M по направлению l
(т.е. скорость изменения значений
функции при движении в данном направлении)
равна скалярному произведению градиента
функции в точке M и единичного
вектора, задающего направление
:
.
Градиент задает направление наибольшего роста значений функции в данной точке, и производная по направлению градиента равна модулю градиента.
Пример 9. Дана функция
.
Найти скорость и направление максимального
роста функции в точке M (2,1,0) и
производные по направлению от точки М
к точке N (1,2,2) и по направлению
{2,1 – 2}.
Решение. Так как
,
то направление максимального роста и его скорость
.
Направление от точки M к N задается вектором
.
Производная по этому направлению
,
т.е. функция убывает в этом направлении.
Для направления, заданного вектором
,
имеем
,
а производная по этому направлению
,
т.е. функция возрастает в этом направлении.
Если поверхность S задана неявно
уравнением
,
то уравнение касательной плоскости к
этой поверхности в точке
имеет вид
,
а уравнение нормали (т.е. прямой, перпендикулярной касательной плоскости) имеет вид
