Уравнение Бернулли и примеры его практического использования

Уравнение Бернулли позволяет решить задачу о полном давлении в любом сечении трубки тока и о составляющих этого давления.

Рис.6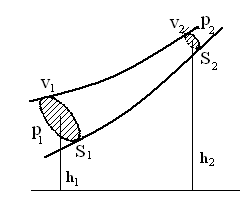

Рассмотрим трубку тока, расположенную наклонно в поле тяготения (рис.6). Выберем два произвольных сечения и , находящихся на разных высотах по отношению к линии горизонта, и - статические давления, соответственно, слева от сечения и справа от сечения . Допустим, что > . Полная энергия некоторой массы жидкости слагается из кинетической энергии и

потенциальной энергии . Поэтому можно записать .

Изменение полной энергии при перемещении массы жидкости из сечения в сечение определится выражением

- (4)

В нашем случае полная энергия увеличивается, т.к. увеличивается и потенциальная энергия (жидкость поднимается до ), и кинетическая (жидкость втекает в сужение, и ее скорость возрастает от V₁ до V₂).

Перемещение жидкости осуществляется вследствие разности давлений . Работа по перемещению жидкости определяется соотношением (3).

На основании закона сохранения энергии можно утверждать, что увеличение полной энергии равно работе , совершенной за счет разности сил давления, поэтому можно записать

, (5)

или после деления (5) на объем получим

,

где - плотность жидкости.

Сгруппируем члены с одинаковыми индексами по обе стороны равенства, получим

. (6)

Так как сечения выбраны нами произвольно, равенство (6) можно записать для любых сечений трубки тока и т.д. Поэтому (6) можно представить в виде

.

Полученное уравнение носит название уравнения Бернулли.

Уравнение выведено в 1738 году Даниилом Бернулли (1700-1782), швейцарским математиком, членом Петербургской Академии наук.

Первое слагаемое называют гидродинамическим давлением, оно возникает вследствие движения жидкости со скоростью ; слагаемое - давление, обусловленное положением частиц жидкости в гравитационном поле Земли; слагаемое р – статическое давление (напор). Сумма получила название гидростатического давления.

Уравнение Бернулли можно сформулировать следующим образом:

в стационарно текущей идеальной жидкости сумма гидростатического и гидродинамического давлений для любого сечения трубки тока есть величина постоянная .

Сумму гидростатического и гидродинамического давлений называют полным давлением. Таким образом, полное давление во всех сечениях трубки тока является одинаковым.

Рассмотрим некоторые следствия, вытекающие из уравнения Бернулли, и примеры практического использования этого уравнения.

а) Пусть жидкость течет так, что во всех точках скорость течения имеет одинаковую величину ( ).

Тогда уравнение (6) принимает вид

,

или

(8)

т.е. распределение давления в этом случае будет таким же, как и в покоящейся жидкости.

б) Для горизонтальной трубки тока уравнение (6) принимает вид

, (9)

или

(10)

Из условия (10) следует, что статическое давление р больше там, где меньше динамическое , и наоборот. Таким образом, статическое давление всегда меньше в узких частях трубки ( ~ ~ ).

Если давление в широкой части трубки атмосферное, то в узкой части, где большая скорость, оно меньше атмосферного. Струя тогда будет оказывать засасывающее действие. На засасывающем действии суженной струи основана работа целого ряда физических и технических приборов – водоструйных насосов, ртутных насосов, инжекторов, пульверизаторов, ингаляторов, карбюраторов и т.д.

Важное практическое применение уравнения Бернулли нашло в приборах для изменения давления и для определения скорости потока.

Поместим в стационарный поток жидкости изогнутую под прямым углом манометрическую трубку 1 с отверстием, обращенным навстречу потоку (рис.7 ).

Рис.7

Такую трубку называют трубкой Пито. Рассмотрим линию тока АВ, проходящую через центр сечения трубки Пито и «упирающуюся» в точку В.

Линию тока можно рассматривать как трубку тока с пренебрежимо малым сечением. Строго говоря, уравнение Бернулли будет справедливо для любой линии тока. Для линии АВ запишем его в виде

(11)

Скорость в точке A равна скорости стационарного потока жидкости V, а скорость в точке В равна нулю, поэтому уравнение Бернулли для линии АВ принимает вид

(12)

Следовательно, давление в точке В равно сумме динамического и статического р давлений в потоке жидкости и жидкость в трубке Пито поднимается до высоты , соответствующей сумме динамического и статического давлений. Таким образом, высота определяет полное давление в потоке.

Если в поток поместить трубку 2, сечение которой параллельно линиям тока (такую трубку называют зондом) (рис.7), то жидкость в ней поднимается на высоту , соответствующую статическому давлению в потоке. По разности можно определить величину динамического давления.

Прибор, сочетающий в себе трубку Пито и зонд (рис.8), получил название дифференциального манометра, или трубки Прандтля. Такой манометр позволяет определить статическое, динамическое и полное давления.

Рис.8

Аналогичные приборы используются для определения скорости потока жидкости (или газа).