4.3. Графіки тригонометричних функцій
Основними
тригонометричними функціями є функції
,
,
,
.
Графіки цих функцій наведено на рис. 4.13
– 4.16.
Рис. 4.13
Рис. 4.14
Рис. 4.15 Рис. 4.16
4.4. Графіки показникової та логарифмічної функцій
Означення.
Функція
вигляду
де
– будь-яке додатне число, що не дорівнює
,
а
–
будь-яке дійсне число, називається
показниковою.
Графіки показникової функції для значень
і
наведено на рис. 4.17.
Рис. 4.17 Рис. 4.18
Означення.
Функція
вигляду
де
і
,
називається логарифмічною.
Графіки логарифмічної функції для
значень
і
наведено
на рис. 4.18.
4.5. Графіки обернених тригонометричних функцій
Оберненими
тригонометричними функціями
називаються функції
,
,
,
.
1.
.
Область визначення функції:
область змінювання функції –
Ця функція – обернена до функції
.
Графік функції наведено на рис. 4.19.
Основні тототожності:
Рис. 4.19 |
Рис. 4.20 |
2.
.
Область визначення функції:
область змінювання функції –
,
.
Ця функція – обернена до функції
.
Графік функції наведено на рис. 4.20.
Основні тототожності:
3.
.
Область визначення функції:
,
область змінювання функції –
,
– горизонтальні асимптоти при
.
Ця функція – обернена до функції
,
.
Графік функції наведено на рис. 4.21.
Основні тототожності:
4.
.
Область визначення функції:
,
область змінювання функції –
,
;
і
– горизонтальні асимптоти при
і
відповідно. Ця функція – обернена до
функції
.
Графік функції наведено на рис. 4.22.
Основні тототожності:
Рис. 4.21 Рис. 4.22
Приклад
4.8.
Побудувати графік функції
.
Розв’язання.
Оскільки
,
то
Таким чином,
.
Графіком цієї функції є напівколо
одиничного радіуса, розташоване у
верхній півплощині (рис. 4.23).
Рис. 4.23
4.6. Побудова графіків функцій за допомогою геометричних перетворень
У табл. 4.4
показано, як за допомогою геометричних
перетворень (паралельний перенос,
симетрія, стиск і розтяг) можна отримати
графіки відповідних функцій з графіка
функції
Таблиця 4.4
Функція |
Перетворення |
Приклад |
|
паралельне
перенесення графіка функції
|
|
|
паралельне перенесення графіка функції на b одиниць вниз (якщо « ») або вгору (якщо «+»)
|
|
на a
одиниць вправо (якщо «
»)
або вліво (якщо «+»)
Закінчення табл. 4.4
Функція |
Перетворення |
Приклад |
|
стиск
або розтяг графіка функції
уздовж осі
|
|
|
стиск
або розтяг графіка функції
уздовж осі
|
|
|
симетрія графіка функції відносно осі |
|
|
симетрія графіка функції відносно осі |
|
(розтяг – якщо
,
стиск – якщо
)
(стиск – якщо
,
розтяг – якщо
)
Приклад
4.9. Побудувати
графік дробово-лінійної функції
.
Розв’язання: Виділимо
цілу частину:
.
Отже, функція набуває вигляду
.
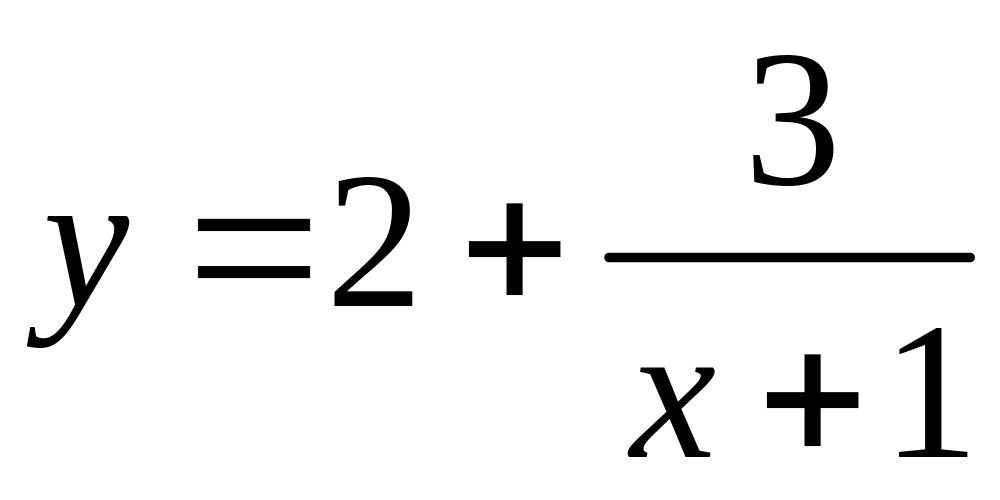Графік (рис. 4.24) цієї функції можна
побудувати з графіка
за допомогою ланцюжка елементарних
перетворень (див. табл. 4.2), а саме:
.
Зауваження.
Під час останніх двох перетворень треба
перенести асимптоти
і центр симетрії
Приклад
4.10.
Побудувати графік функції
Розв’язання. Графік цієї функції (рис. 4.25) можна отримати з графіка функції
(див.
рис. 4.13) в результаті розтягнення
останнього в два рази вздовж осей
і
Рис. 4.24
Рис. 4.25
Приклад
4.11.
Побудувати графік функції
.
Розв’язання.
Перепишемо функцію у вигляді
У системі координат
(пунктирні лінії) побудуємо графік
функції
,
а потім вісь
перенесемо на одиницю вниз (вісь
),
а вісь
– на
ліворуч (рис. 4.26).
Приклад
4.12.
Побудувати графік функції
.
Розв’язання.
Отримаємо
цей графік з графіка
перенесенням уздовж осі
на одиницю вліво (рис. 4.27).
Рис. 4.26
Рис. 4.27
Приклад
4.13.
Побудувати графік функції
Розв’язання.
Графік
цієї функції отримаємо з графіка функції
перенесенням на одиницю вправо вздовж
осі
.
Пряма
– вертикальна асимптота (рис. 4.28).
Завдання для самостійної роботи
4.1. Знайти область визначення функції:
а)
;
b)
;
c)
;
d)
; e)
;
f)
;
g)
.
4.2. Дослідити функцію на парність або непарність:
а)
b)
c)
d)
e)
f)
.
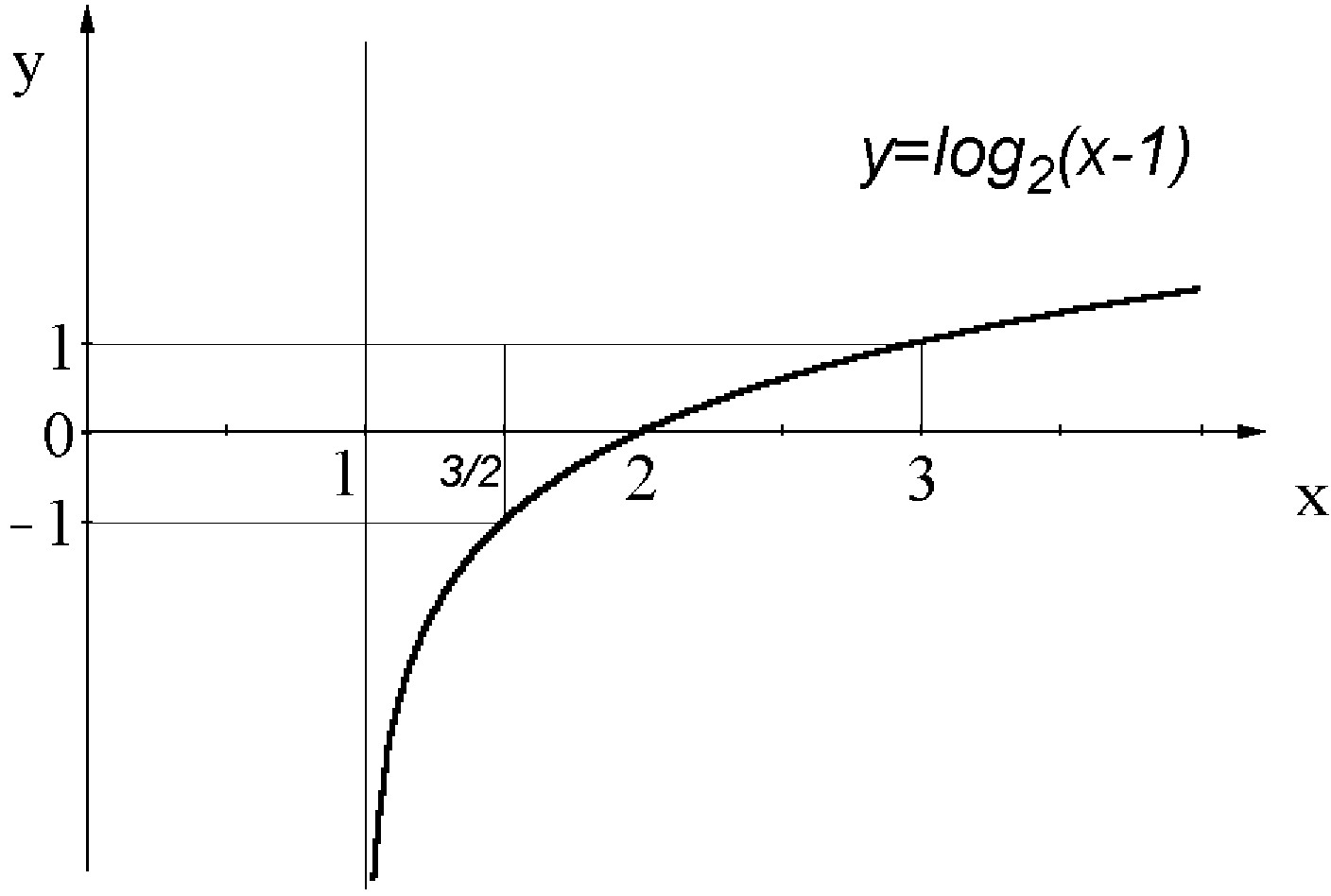
Рис. 4.28
4.3. Побудувати графіки функцій:
а)
;
b)
;
c)
;
d)
.
4.4. Побудувати графіки функцій:
а)
b)
c)
d)
e)
f)
g)
h)
i)
j)
к)
l)
м)
n)
4.5. Побудувати графіки функцій:
а)
b)
c)
d)
e)
;
f)
g)
h)
i)
j)
k)
l)
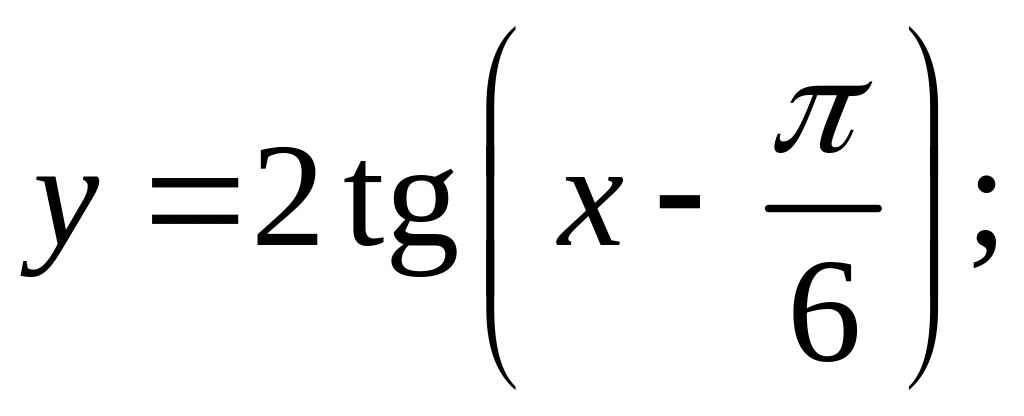m)
4.6. Побудувати графіки функцій:
а)
;
b)
;
c)
;
d)
;
e)
.
Розділ 5. РІВНЯННЯ ТА НЕРІВНОСТІ