2.2. Основні формули тригонометрії. Формули зведення. Перетворення тригонометричних виразів

У процесі перетворення тригонометричних виразів широко застосовуються такі формули.

1. Формули додавання:

.

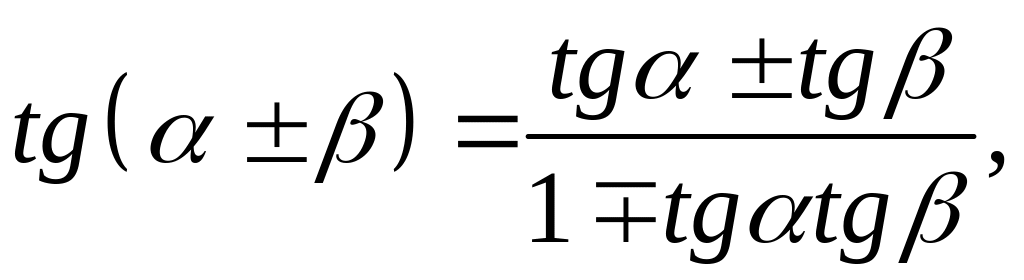
2. Формули кратних аргументів:

3. Формули половинного аргументу:

4. Формули перетворення суми і різниці в добуток:

5. Формули перетворення добутку в суму і різницю:

6. Співвідношення між , , :

.

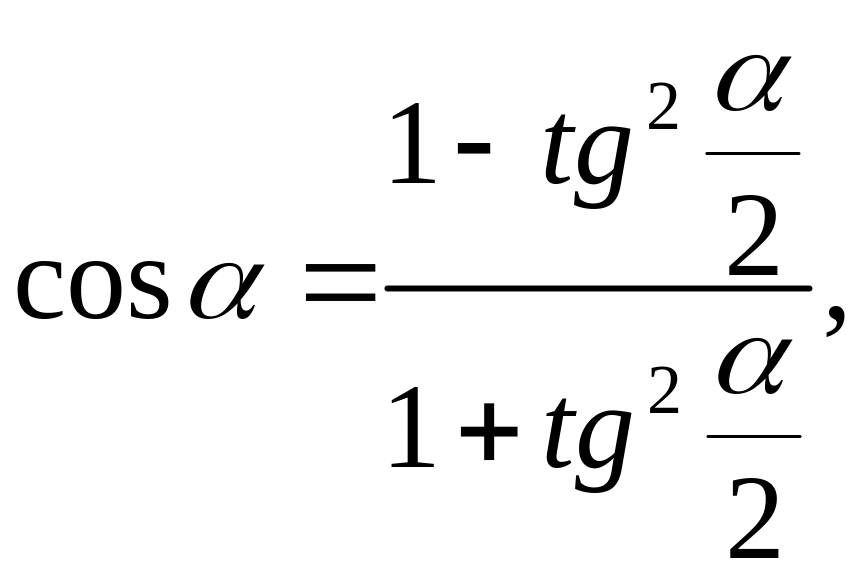
Також мають місце формули зведення. Формули зведення перетворюють тригонометричні функції від аргументів до функцій з аргументом .

Для зручності у користуванні формулами зведення використовують такі правила:

а) кут завжди вважається гострим;

б) ціле число періодів завжди можна відкинути;

в) якщо кут відкладається від горизонтального діаметра , то назва функції зберігається; якщо кут відкладається від вертикального діаметра , то назва функції змінюється (синус – на косинус, косинус – на синус, тангенс – на котангенс, котангенс – на тангенс).

Приклад 2.4. Спростити вираз .

Розв’язання. Для отримання розв’язку скористаємося формулами зведення (див. табл. 2.1) та властивостями парності й непарності тригонометричних функцій. Маємо

.

Приклад 2.5. Обчислити число .

Розв’язання. Для отримання розв’язку скористаємося формулами зведення (див. табл. 2.1) та формулами додавання. Маємо

Приклад 2.6. Обчислити якщо і .

Розв’язання. Скористаємося формулами і візьмемо . Маємо 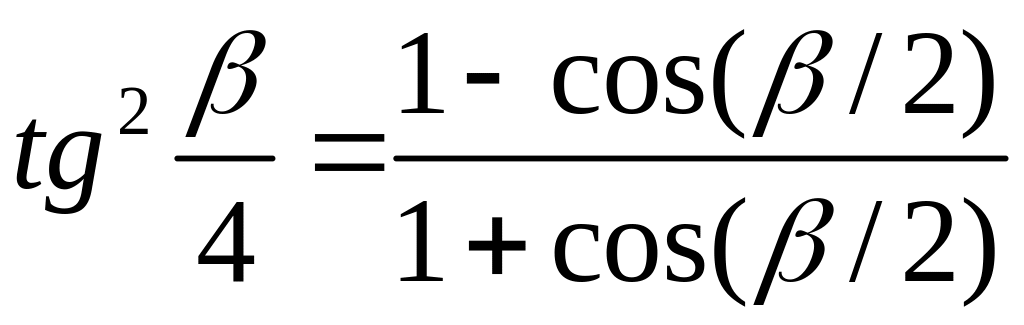, і задача зводиться до обчислення . Проведемо ці обчислення:

; оскільки , то і тому . Значить, . Таким чином, . Кут , тому і

Приклад 2.7. Обчислити , якщо .

Розв’язання. Скористаємося формулою перетворення добутку тригонометричних функцій в суму і формулою подвійного аргументу для . Маємо

Приклад 2.8. Довести рівність .

Розв’язання. Скористаємося формулами для перетворення суми і різниці синусів у добуток, а також формулами подвійного аргументу для і . Маємо

Приклад 2.9. Обчислити

Розв’язання. Скористаємося формулою для синуса суми двох аргументів і табличними значеннями тригонометричних функцій. Маємо

Приклад 2.10. Довести тотожність

Розв’язання. У лівій частині наведеної рівності виділимо повний куб і квадрат. Маємо

Приклад 2.11. Довести тотожність .

Розв’язання. До лівої частини рівності застосуємо формулу різниці квадратів, а до правої – формулу косинуса різниці двох аргументів. Маємо

.

Ліву та праву частини запропонованої рівності зведено до однакового вигляду, тому вони рівні.

Приклад 2.12. Довести тотожність .

Розв’язання.

У перетвореннях тригонометричних виразів застосовувалися формули подвійного аргументу для і . Слід звернути увагу на те, що наведені дії можливі лише тоді, коли тобто , або .

Приклад 2.13. Довести тотожність .

Розв’язання. Розкладемо на множники ліву частину рівності та застосуємо формули тангенса суми і різниці двох аргументів. Маємо

.

Доведена тотожність виконується, якщо , тобто .

Приклад 2.14. Довести числову рівність .

Розв’язання. Помножимо та поділимо ліву частину рівності на і скористаємося формулами подвійного аргументу. Маємо

.

Завдання для самостійної роботи

Обчислити значення тригонометричних виразів:

2.08. , якщо . 2.09. , якщо .

2.10. , якщо . 2.11. , якщо і .

Спростити:

2.12. . 2.13. .

2.14. .

2.15. .

2.16. . 2.17. .

Довести тотожності:

2.18. . 2.19. .

2.20. .

2.21. . 2.22. .

2.23. 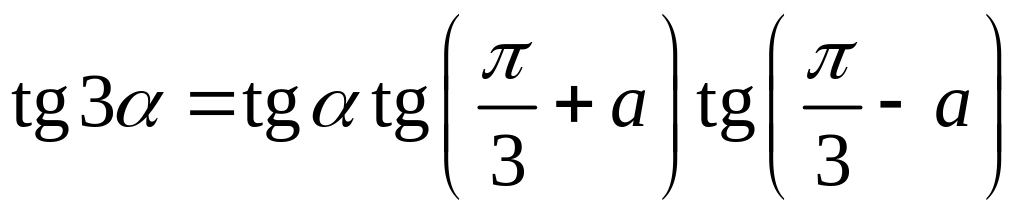. 2.24. .

2.25. . 2.26. .

З’ясувати, для яких значень мають місце рівності:

2.27. . 2.28. .

У подальшому нам знадобиться означення ще чотирьох функцій числового аргументу.

Нехай число належить проміжку . Арксинусом числа ( ) називається таке число (або така дуга , або такий кут ) із відрізка , синус якого дорівнює . Таким чином, запис означає, що

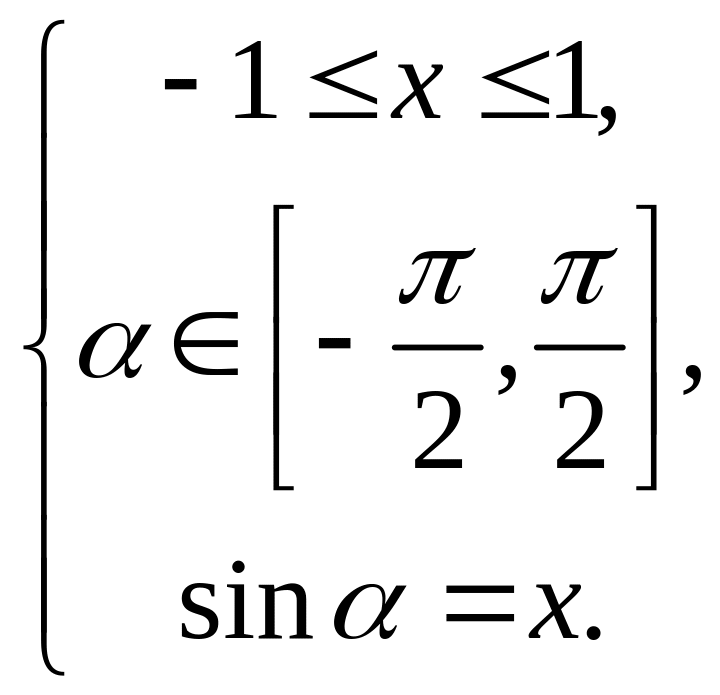
Арккосинусом числа ( ) називається таке число (або така дуга , або такий кут  ) із відрізка , косинус якого дорівнює . Отже, запис означає, що

Нехай . Арктангенсом числа називається таке число (або така дуга , або такий кут ) із інтервалу , тангенс якого дорівнює числу . Аналогічно попереднім записам маємо: означає, що

Арккотангенсом числа називається таке число (або така дуга , або такий кут ) із інтервалу , котангенс якого дорівнює . Отже, означає, що

Корисною є табл. 2.2 найпростіших значень функцій.

Таблиця 2.2

Функція	Аргумент
							–
							–

Зауваження. Позначення функцій пов’язано зі змістом слова « »- «арка», або «дуга».

Наведемо деякі тотожності, зв’язані із

1) 2)

3) 4)

5) 6) .

Приклад 2.15. Обчислити .

Розв’язання. Треба знайти , якщо відомо, що . Кут розташований у першій чверті і має додатний косинус. Тому .

Приклад 2.16. Обчислити .

Розв’язання. За формулою знайдемо . Важливо зауважити, що за означенням арктангенса цей кут розташований у першій або четвертій чверті і має додатне значення косинуса, тобто .

Приклад 2.17. Обчислити .

Розв’язання. Оскільки За допомогою формул зведення перетворюється на

Аргумент Остаточно

Завдання для самостійної роботи

2.29. Обчислити значення: a) , b) , c) , d) , e) , f) , g) , h) .

2.30. Катети прямокутного трикутника дорівнюють і . Знайти один із його гострих кутів , користуючись по черзі чотирма оберненими тригонометричними функціями.

Спростити вирази:

2.31. а) ; b) ;

c) ; d) ; .

2.32. а) ; b) ; c) .

2.33. а) , b) , c) .

2.34. Обчислити: а) , b) , c) ,

d) , e) , f) , g)

2.35. Довести, що , якщо .

Розділ 3. ПЕРЕТВОРЕННЯ ЛОГАРИФМІЧНИХ ВИРАЗІВ