Розділ 2. Тригонометричні перетворення

2.1. Тригонометричні функції числового аргументу

Наведемо означення тригонометричних функцій числового аргументу.

С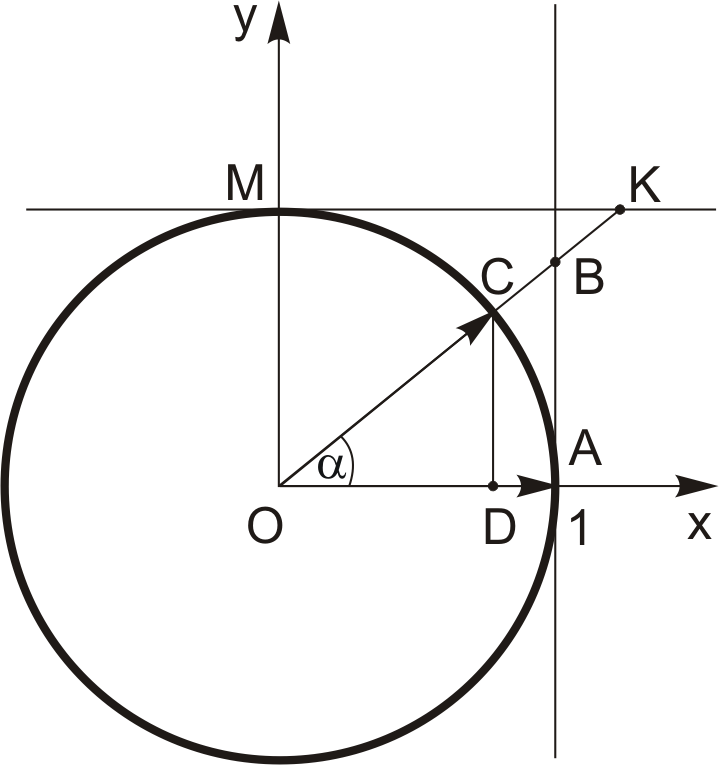 инусом числа ( ) називається ордината точки C, яка утворюється в результаті повороту радіус-вектора = {0,1} на кут радіан. Якщо , то поворот здійснюється проти ходу годинникової стрілки і вважається додатним, а якщо , то поворот – від’ємний і здійснюється за ходом годинникової стрілки.

Косинусом числа ( ) називається абсциса точки С.

Тангенсом числа ( ) називається ордината точки В, яка розташована на перетині продовження радіус-вектора з віссю тангенсів (пряма, проведена через точку А(1,0) перпендикулярно до осі ОХ).

Котангенсом числа ( ) називається Рис. 2.1

абсциса точки К, яка лежить на перетині продовження радіус-вектора з віссю котангенсів (пряма, проведена через точку М(0,1) перпендикулярно до осі ОY).

Іноді використовуються ще дві тригогонометричні функції, а саме секанс числа ( ) і косеканс числа ( ). Ці функції вводяться таким чином:

, .

Між тригонометричними функціями кута існують прості співвідношення:

; , ;

, ; , ;

, ; , .

набуває додатних значень у першій ( ) та другій ( ) чвертях і від’ємних – у третій ( ) та четвертій ( ); набуває додатних значень у першій та четвертій чвертях і від’ємних – у другій та третій; і – додатних у першій та третій чвертях і від’ємних – у другій та четвертій (рис. 2.2).

Згідно з означенням тригонометричних функцій мають місце такі формули:

, , ,

, ,

Рис. 2.2

для будь-якого значення і

, , ,

для будь-якого допустимого значення .

Табличні значення тригонометричних функцій гострих кутів наведено в табл. 2.1.

Таблиця 2.1

Функція	Кут : радіани (градуси)
					–
	–

Приклад 2.1. Визначити знаки таких виразів: а) б)

в) де .

Розв’язання: а) кут належить другій чверті, тому ; б) кут належить першій чверті, тому ; в) значення кута не перевищує , тому вираз належить другій чверті. Синус і косинус кутів другої чверті мають різні знаки, тому .

Приклад 2.2. Обчислити

Розв’язання. Аргументи тригонометричних функції – табличні. Значення тригонометричних функцій від цих аргументів – відомі, а саме:

Тому

Приклад 2.3. Обчислити , якщо і .

Розв’язання. Оскільки , то або Оскільки , то

Завдання для самостійної роботи

2.01.Побудувати кут: 1) синус якого дорівнює: a) b) c) 2) косинус якого дорівнює: a) b) c) 3) тангенс якого дорівнює: a) b) c) котангенс якого дорівнює: a) b) c) .

2.02. Визначити знаки таких виразів: а) b) c)

d) e) , де f) , де

g) h)

2.03.Обчислити: а) b)

c) d)

e) f)

2.04. Для яких чвертей проміжку виконуються нерівності: а)

b) c) d)

2.05. До яких чвертей належить кут, якщо: а) ; b) ; c)

d)

2.06. Чи існує таке значення щоб: а)

b) c) d)

2.07. Обчислити , , , якщо: а) і b) і