5.2. Метод інтервалів. Раціональні нерівності

Розглянемо функцію

Якщо всі нулі чисельника та знаменника відмітити на числовій прямій, то вони розіб’ють її на проміжків. Усередині кожного з них функція неперервна та зберігає знак. Для визначення цього знака достатньо взяти будь-яку точку з цього проміжку та знайти знак функції в цій точці. На практиці для розв’язання нерівності застосовують метод інтервалів.

В основу методу інтервалів покладено такі твердження:

1. Якщо – така точка, що показник степеня для виразу є число непарне, то праворуч і ліворуч від (на сусідніх проміжках) функція має різні знаки.

Наприклад, маємо функцію . При переході через точки функція змінює знак.

2. Якщо – така точка, що показник степеня для виразу є число парне, то праворуч і ліворуч від (на сусідніх проміжках) функція має однакові знаки.

Наприклад, маємо функцію . При переході через точку функція не змінює знак.

Алгоритм розв’язання нерівностей методом інтервалів

1. На числовій прямій позначають всі нулі чисельника і знаменника (критичні точки) заданої функції .

2. Визначають знак нерівності на кожному з числових проміжків. Обов’язково враховують парність чи непарність відповідного показника степеня.

3. Вибирають проміжки згідно зі знаком нерівності:

• якщо функція має знак "+", то на цьому проміжку ;

• якщо функція має знак "-", то на цьому проміжку .

Приклад 5.8. Розв’язати нерівність

Розв’язання.

1. Нулі заданої функції і . Позначимо ці точки на числовій прямій

(рис. 5.1). Оскільки нерівність строга, то точки 3 і 5 виключаємо із розв’язку.

2. Точки 3 і 5 розбивають числову пряму на 3 інтервали:

3. Визначимо знак нерівності на проміжку : нехай , тоді маємо нерівність . Скористаємося правилом зміни знака: на проміжку знак "-"; на проміжку – "+". Виберемо проміжки зі знаком нерівності "+". Тоді .

Рис. 5.1 Рис. 5.2

Приклад 5.9. Розв’язати нерівність .

Розв’язання.

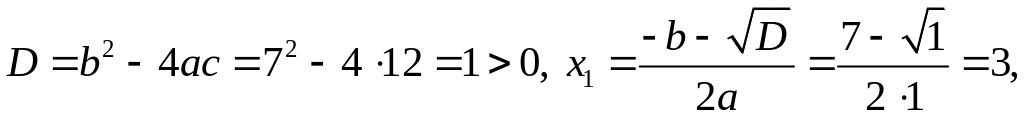
1. Розкладемо квадратний тричлен . Для цього розв’яжемо квадратне рівняння : . Нерівність запишемо у вигляді і застосуємо метод інтервалів.

2. – нулі функції (рис. 5.2).

3. Визначаємо знак нерівності на кожному інтервалі:

: нехай , тоді ;

: нехай , тоді ;

: нехай , тоді .

Виберемо проміжки зі знаком нерівності "-". Маємо .

Приклад 5.10. Розв’язати нерівність .

Розв’язання.

1. Нулі заданої функції – . Вони розбивають числовий інтервал на 4 проміжки (рис. 5.3). Оскільки нерівність не строга, то точки і включаємо до розв’язку.

Рис. 5.3

2. Визначаємо знак нерівності на інтервалі : візьмемо , тоді .

3. Подвійних точок нерівність не має. Тому скористаємося умовою зміни знака: – "+"; – "-"; – "+". Маємо .

Приклад 5.11. Розв’язати нерівність

Розв’язання. ОДЗ: . Відмітимо на числовій прямій точки , (нулі чисельника) і , (нулі знаменника). Нерівність записано в стандартному вигляді, тому праворуч від точки функція додатна. Усі показники степеня непарні, тому при переході через них знак лівої частини нерівності буде змінюватися (рис. 5.4). Маємо

Рис. 5. 4

Завдання для самостійної роботи

5.6. Розв’язати нерівності:

а) ; b) ; c) ;

d) ; e) ; f) ;

g) ; h) ;

i) ; j) ; k) ; l) .