1.5. Системы и базисы булевых функций

Количество различных булевых функций зависит от количества переменных и значности логики. В двузначной логике это количество равно , где n – число переменных булевых функций.

В таблице 4 приведены функции от двух переменных. Перечислим их:

– константа «0»;

– конъюнкция;

– левая коимпликация;

– сохраняющая x₁;

– правая коимпликация;

– функция, сохраняющая x₂;

– сложение по модулю 2, или функция нечетности, или неэквивалентности;

– дизъюнкция;

– функция Вебба;

– эквивалентность, или функция четности, или равнозначности;

– отрицание, инверсия;

– правая импликация («из x₂ следует x₁», «если x₂, то x₁»);

– отрицание, инверсия;

– левая импликация;

– функция Шеффера;

– константа «1».

Различных булевых функций от двух переменных – 16, от трех переменных – 256 и т.д., но все ли они необходимы при составлении логических выражений. Возникает вопрос, можно ли использовать ограниченные совокупности булевых функций для представления логического высказывания любой сложности. Из каких функций эти совокупности должны состоять? Скажем, что такие совокупности функций называются системами и базисами булевых функций.

Определение. Системой булевых функций называется такая их совокупность, с помощью которой можно построить любое логическое выражение, а возможность строить любые логические выражения называется полнотой системы.

Базисом булевых функций называется такая система булевых функций, из которой невозможно удалить ни одной функции без потери этой системой полноты.

Для решения вопроса о том, какая совокупность функций является системой или базисом булевых функций применяется критерий полноты.

1.6. КРИТЕРИЙ ПОЛНОТЫ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ ПОСТА-ЯБЛОНСКОГО

Система S булевых функций f_i является полной тогда и только тогда, когда среди булевых функций найдется

• хотя бы одна 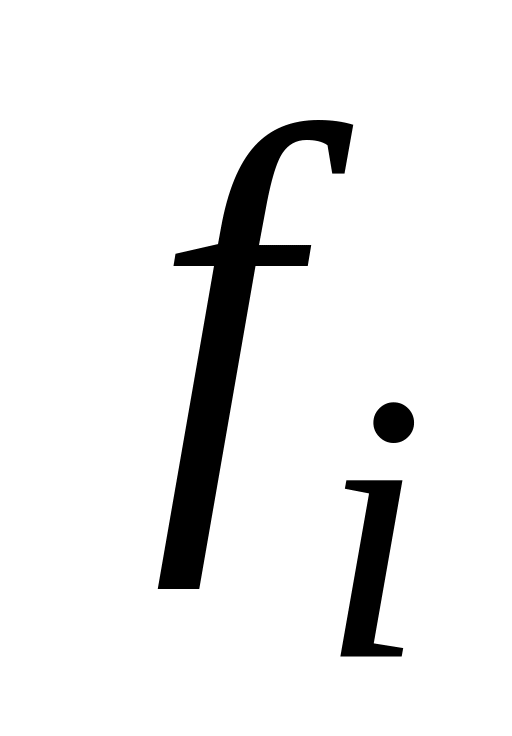, не сохраняющая 0 (не принадлежащая классу К₀);

• хотя бы одна , не сохраняющая 1 (не принадлежащая классу К₁);

• хотя бы одна нелинейная (не принадлежащая классу К_Л);

• хотя бы одна несамодвойственная (не принадлежащая классу К_С);

• хотя бы одна немонотонная (не принадлежащая классу К_М);

Приведем определения свойств булевых функций, принадлежащих пяти вышеперечисленным классам булевых функций.

К лассом К₀ булевых функций называется множество таких, что .

В двузначной логике P₂ таких функций ровно половина, т.е. , так же, как и принадлежащих К₁.

Классом К₁ булевых функций называют множество таких, что .

Классом К_Л линейных булевых функций называют множество функций таких, что ,

где – коэффициенты, определяемые для ,

– сумма по модулю 2,

– полином Жегалкина.

Классом К_С самодвойственных булевых функций, называются такие , для которых на противоположных наборах переменных и значения функций также противоположны .

Число самодвойственных функций от n-переменных (n–1, так как противоположных пар входных наборов в 2 раза меньше, чем ).

Классом К_М монотонных БФ называется множество таких , у которых значения функции на сравниваемых наборах при том, что сравниваемые наборы k и l являются склеиваемыми

.

Определим, является ли полной система, состоящая из функции .

			#
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

K₀:

K₁:

K_Л:

Определим неопределенные коэффициенты, начиная с c₀ на нулевом наборе.

можно определить на наборе (100), когда полином сокращается до из-за значений x₂ и x₃, равных 0.

Аналогично поступим при определении и .

Проверим соответствие значений полинома с вычисленными коэффициентами значениям функции на всех остальных наборах (или для доказательства принадлежности к - нелинейным функциям - до первого несоответствия).

К_С: самодвойственность определяется по таблицам истинности, где противоположные наборы расположены симметрично середине таблицы:

(000)↔ (111) , (001) ↔ (110) , (101) ↔ (010) и т.д.

Значения функции также должны быть противоположны относительно середины:

на наборах (000) и (111) свойство самодвойственности выполняется.

на наборах (011) и (100) свойство самодвойственности не выполняется .

К_М: для определения монотонности воспользуемся графом функции # (геометрической интерпретацией булевых функций)

0 111 уровень 3

( 3 единицы)

1 10 0 0 101 0 011 уровень 2

( 2 единицы)

1 00 0 0 010 0 001 уровень 1

( 1 единица)

1 000 уровень 0

(0 единиц в

двоичном

наборе)

Распределение вершин графа по уровням с одинаковым количеством единиц позволяет увидеть, что сравниваемые наборы находятся на соседних уровнях. Например, (001) и (011) или (101) и (111) и связаны между собой ребрами (0_1) и (1_1) соответственно. Не сравнимыми будут наборы противоположные или с несмежных уровней ((010) и (101) или (000) и (011)).

Монотонные наборы: # (100) ≤ # (101),

# (110) ≤ # (111) и т.д.

Наличие хотя бы одной пары немонотонных наборов обозначает немонотонность функции. То есть .

Итак, не принадлежит ни к одному классу булевых функций, и, следовательно, сама составляет базис булевых функций { # }.