1.1.Булева алгебра

Булеву алгебру составляют два множества – множество операторов или булевых функций и множество значений, к которым эти операторы применяются. В двузначной логике множество значений состоит из множеств {0, 1} или {И, Л}, а множество функций из некоторого набора функций f_j .

Булевой функцией (БФ) или функцией алгебры логики f_j(x₁, x_2, … x_n) называется отображение n-мерного пространства {0, 1}ⁿ значений аргументов в одномерное пространство {0, 1} значений функции под действием f_i:

f_j

{ 0, 1}ⁿ {0, 1}.

Таким образом, область определения БФ – n-мерное пространство {0, 1}ⁿ, где n – количество переменных функции, а область значений БФ – одномерное пространство {0, 1}.

По количеству переменных различают функции:

• ноль-местные - 0, 1;

• одноместные - 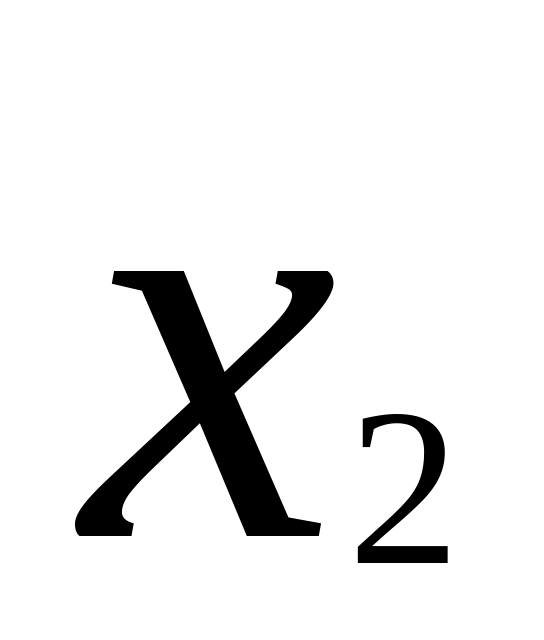или ;

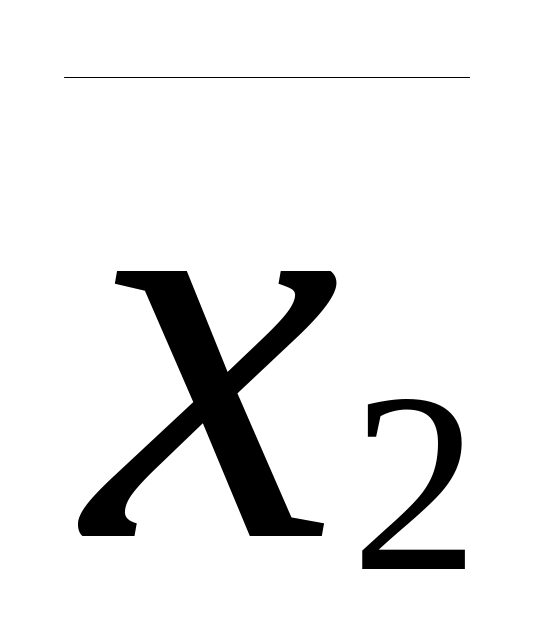• двухместные х₁&x₂ или х₁х₂;

• n-местные - # (x₁,x₂,…x_n).

Существует несколько способов задания БФ:

• в табличном представлении;

• через перечисление десятичных эквивалентов двоичных наборов;

• в виде логического выражения.

В табличном представлении для каждого i-го набора входных переменных в таблице указано значение функции на этом наборе (рис. 1).

Десятичный эквивалент i	x1x2x3	fi
0	0 0 0	1
1	0 0 1	0
2	0 1 0	1
3	0 1 1	0
4	1 0 0	0
5	1 0 1	0
6	1 1 0	1
7	1 1 1	1

Рис.1 Булева функция f в табличном представлении

При перечислении десятичных эквивалентов двоичных наборов достаточно перечислить только единичные или только нулевые наборы данной функции. Функция с рис.1 , задана таким способом - =(0,2,6,7)₁. Оставшиеся наборы -1,2,4,5 – считаем определенными в 0.

Для задания функции в виде логического выражения, т.е. через другие БФ, например =  , где использованы функции ,,, необходимо условиться о работе этих функций. Приведем таблицы истинности функций -конъюнкции, -дизъюнкции, -отрицания:

Таблица 1 Таблица 2 Таблица 3

-конъюнкция -дизъюнкция -отрицание

логическое «И» логическое «ИЛИ» логическое «НЕ»

						
0	0	0		0	0	0		0	1
0	1	0		0	1	1		1	0
1	0	0		1	0	1
1	1	1		1	1	1

n- мерные наборы значений переменных БФ называются кортежами. Например, нулевым значениям функции f на рис.1 соответствуют 4 кортежа входных переменных (001), (011), (100), (101). В геометрической интерпретации кортежи представляют собой точки пространства, мерность которого определяется количеством переменных данной функции, а координаты – значениями переменных. Значения самой функции на соответствующих наборах переменных приписаны вершинам. На рис.2 показана геометрическая интерпретация булевой функции из таблицы истинности рис.1.

Х₂

1 010 1 110

0 011 1 111

Х₁

1 000 0 100

Х₃ 0 001 0 101

Рис. 2. Булева функция f от трех переменных в геометрической интерпретации.

1.2.ДОКАЗАТЕЛЬСТВА РАВЕНСТВА БУЛЕВЫХ ФУНКЦИЙ.

Существует два способа доказательства равенства булевых функций:

1. С помощью таблиц истинности;

2. С помощью основных законов алгебры логики.

Таблица истинности является основным методом при доказательстве тождеств.

Назовем тождеством такое равенство, которое справедливо для любых значений переменных. Так, выражение является равенством только на наборе x₁=0 и x₂=0. На всех остальных наборах равенство не справедливо. Т. е. не тождество.

Пример 1. Доказать, что является тождеством.

Доказательство. Строим таблицу истинности для 2-х переменных и вычисляем значения для правой и левой частей равенства.

0 1 0 1 1	0 1 1 1	1 0 0 0	1 1 0 0	1 0 1 0	1 0 0 0

Т. к. результаты вычислений правой и левой частей выражения одинаковы на всех наборах, то данное равенство является тождеством.

1.3.ОСНОВНЫЕ ЗАКОНЫ БУЛЕВОЙ АЛГЕБРЫ

В булевой алгебре существует система тождеств, применяемых для преобразований выражений или для вычисления их значений без использования таблиц истинности. Эти тождества называются основными законами булевой алгебры. Перечислим их:

Закон идемпотентности:

Закон коммутативности:

Закон ассоциативности:

Закон дистрибутивности:

Закон склеивания:

Закон поглощения:

Закон де Моргана:

Закон двойного отрицания:

Законы для действий с константами: ;

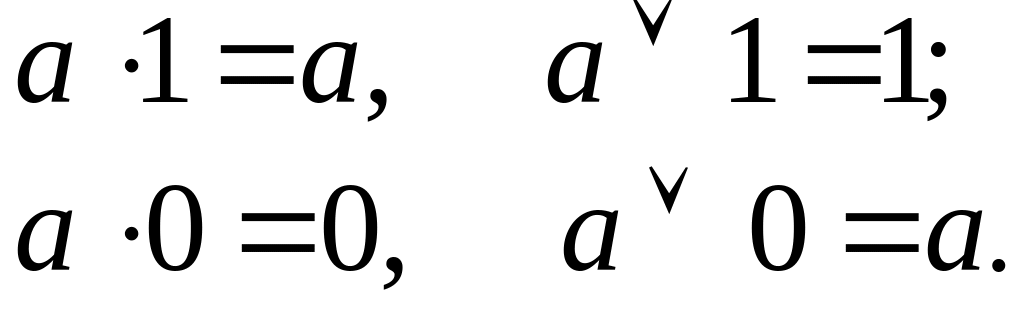
Видно, что часть законов аналогична законам линейной алгебры как, например, дистрибутивность для умножения и невозможна в линейной алгебре – – дистрибутивность для сложения.

Пример 2. Сократить выражение, используя основные законы алгебры логики

В решении использованы закон де Моргана и закон поглощения. При решении задач на преобразование выражений необходимо учитывать порядок действий, который определяется приоритетом функции и может быть изменен использованием скобок.

1.4.О КОЛИЧЕСТВЕ ДВОИЧНЫХ НАБОРОВ БУЛЕВЫХ ФУНКЦИЙ И КОЛИЧЕСТВЕ БУЛЕВЫХ. ФУНКЦИЙ ОТ N-ПЕРЕМЕННЫХ

В таблице на рис.1 трехмерные наборы расположены в порядке возрастания их номеров в двоичном коде начиная с номера ноль и заканчивая номером семь в десятичной системе счисления - 0₍₁₀₎ = 000₍₂₎ 7₍₁₀₎ = 111₍₂₎. Начальный набор, состоящий только из нулей, в таблицах функций принято называть нулевым набором, а последний, состоящий только из единиц - единичным. Двоичный набор полностью определяется своим номером и своей размерностью.

Пример 3. «Значение функции от 5 переменных равно 1 на 4-м наборе» означает, что f(0,0,0,1,1)=1,а не f(1,1)=1 или f(0,1,1)=1, хотя все двоичные наборы (00011), (11) и (011) одинаково равны десятичной тройке.

Наборы n-ой размерности пронумеруем целыми числами от 0 до 2ⁿ-1, откуда следует зависимость: для функции от n переменных имеется точно 2ⁿ двоичных n-мерных наборов (n=1, 2,…).

Подсчитаем число различных булевых функций от n переменных. В качестве примера рассмотрим сначала функции от двух переменных и построим таблицу всех возможных функций (табл. 4).

Таблица 4

x1x2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
00	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
01	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
10	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
11	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Принцип построения каждой новой функции такой же, как и при построении каждого нового набора – десятичный номер набора или функции соответствует их двоичным кодам. Следовательно, количество функций, как и наборов, определяется количеством двоичных разрядов как 2^k,

где k=2ⁿ – для определения количества функций,

k=n – для определения количества исходных наборов функций (n-количество переменных функции).

Отсюда следующая зависимость: для функции от n

переменных имеется точно различных булевых функций (n=1,2,…)

Порядок действий определяется приоритетом функций, и может быть изменен с помощью скобок.

Функции в порядке убывания приоритета: –, &, .

В приведенных ниже примерах а и б сносками с номерами показан порядок действий.

2 3 4 2 1 4 3 6 5

а ) ; б)

1

Задача 1. Вычислить значения выражений а и б на всех наборах переменных.

x1x2x3	a) 1	а) 2	a) 3	a) 4	б) 1	б) 2	б) 3	б) 4	б) 5	б) 6
0 0 0	0	1	0	0	1	1	1	1	1	1
0 0 1	0	1	1	1	1	1	0	0	1	1
0 1 0	0	1	0	1	0	0	1	0	1	1
0 1 1	0	1	1	1	0	0	0	0	1	1
1 0 0	0	1	0	0	1	1	1	1	0	1
1 0 1	0	1	1	1	1	1	0	0	0	0
1 1 0	1	0	0	1	0	1	1	1	0	1
1 1 1	1	0	0	1	0	1	0	0	0	0