2.3 Перевірка адекватності побудованих рівнянь регресії
Підрахований програмою коефіцієнт детермінації не зовсім вірний. Він вважається правильно тільки для лінійної регресії. У стовпцях праворуч від діаграми проведемо правильні розрахунки і перевіримо адекватність рівняння регресії по Фішеру:
1) Підрахуємо коефіцієнт детермінації по формулі:
|
(2.1) |
.
2)
У стовпці AF9:AF18 обчислимо по записаному
на діаграмі рівнянню регресії теоретичні
значення фактора Y,
вони позначені
.
3) У стовпці AG9:AG18 підрахуємо різниці теоретичним та експериментальним значенням фактора Y з а формулою
|
(2.2) |
4) У ячкйці AF24 програмуємо формулу виду (2.1) для коефіцієнта детермінації. Для чисельника використовуємо функцію «СУММКВ».
5) У ячейку AG28 вводимо m – число коефіцієнтів, які присутні в рівнянні регресії.
6) У ячейці AG31 підраховуємо спостережуване значення критерію Фішера за формулою:
|
(2.3) |
7) Абсолютно аналогічно відпрацьовується решта всіх варіантів рівняння регресії, запропоновані в меню.
2.4 Порівняння отриманих рівнянь регресії
Після того, як оброблено всі шість діаграм, необхідно занести отримані значення для коефіцієнта детермінації і для критерію Фішера в таблицю в кінці роботи.
Проаналізувати результати і вибрати ту лінію регресії, яка найвдаліше описує експериментальні дані.
На відведених полях в кінці роботи записати загальний висновок, вибране рівняння і відповідний коефіцієнт детермінації.
3 Варіанти початкових даних для лабораторної роботи № 2
Таблиця 2.1
|
Варіант |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
1 |
2,2 |
17,2 |
16,0 |
2,2 |
7,8 |
6,0 |
3,4 |
5,7 |
13,0 |
11,2 |
2 |
2,5 |
14,1 |
12,7 |
5,4 |
7,4 |
5,2 |
6,0 |
3,5 |
32,0 |
14,5 |
3 |
2,8 |
10,7 |
10,0 |
8,7 |
8,7 |
5,4 |
10,8 |
5,0 |
59,2 |
17,6 |
4 |
4,6 |
10,4 |
8,4 |
10,5 |
8,5 |
4,2 |
11,0 |
10,0 |
74,2 |
23,7 |
5 |
5,5 |
8,0 |
7,3 |
11,4 |
11,4 |
4,0 |
13,0 |
8,4 |
69,7 |
26,5 |
6 |
7,4 |
7,4 |
7,8 |
12,7 |
13,9 |
3,6 |
13,0 |
10,5 |
80,0 |
31,2 |
7 |
8,6 |
5,5 |
8,6 |
13,7 |
15,1 |
3,1 |
14,8 |
20,8 |
76,0 |
40,8 |
8 |
11,1 |
5,2 |
11,1 |
15,0 |
15,0 |
3,3 |
18,0 |
38,0 |
66,2 |
42,6 |
9 |
14,3 |
3,1 |
14,3 |
15,6 |
15,6 |
3,5 |
22,8 |
40,6 |
78,0 |
46,5 |
10 |
18,2 |
3,8 |
18,2 |
15,8 |
15,8 |
3,7 |
29,8 |
49,4 |
81,2 |
46,5 |
Таблиця 2.2
|
Варіант |
|||||||||
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
X |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
1 |
20,0 |
2,0 |
2,7 |
14,3 |
15,4 |
2,4 |
2,2 |
0,9 |
1,0 |
0,4 |
2 |
12,1 |
5,2 |
4,8 |
10,4 |
9,8 |
3,7 |
4,4 |
4,0 |
2,5 |
0,5 |
3 |
6,5 |
5,6 |
5,4 |
11,2 |
5,6 |
3,7 |
6,4 |
5,4 |
3,8 |
0,7 |
4 |
4,6 |
7,4 |
6,4 |
9,2 |
4,6 |
4,0 |
8,8 |
6,4 |
4,1 |
1,1 |
5 |
1,8 |
10,6 |
6,5 |
8,5 |
2,6 |
5,2 |
9,4 |
7,7 |
4,2 |
1,6 |
6 |
1,2 |
11,3 |
5,8 |
6,9 |
2,1 |
5,2 |
10,2 |
7,4 |
4,6 |
2,2 |
7 |
0,7 |
11,5 |
4,8 |
6,0 |
2,4 |
6,8 |
11,7 |
8,2 |
4,9 |
2,6 |
8 |
0,5 |
12,6 |
4,4 |
5,2 |
2,0 |
8,4 |
12,1 |
8,0 |
4,8 |
4,2 |
9 |
0,8 |
12,5 |
2,6 |
6,0 |
1,4 |
11,3 |
13,3 |
8,5 |
5,2 |
6,8 |
10 |
0,3 |
13,4 |
0,7 |
4,6 |
1,4 |
14,3 |
13,7 |
8,3 |
5,2 |
11,8 |
Таблиця 2.3
|
Варіант |
|||||||||
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
X |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
1 |
4,7 |
0,4 |
13,3 |
2,3 |
3,5 |
11,4 |
19,5 |
1,1 |
12,3 |
14,4 |
2 |
7,8 |
0,5 |
12,0 |
7,6 |
8,0 |
12,5 |
14,5 |
3,9 |
12,0 |
12,5 |
3 |
13,6 |
0,7 |
9,3 |
13,1 |
8,8 |
11,5 |
9,7 |
3,1 |
11,9 |
9,8 |
4 |
15,4 |
1,1 |
8,5 |
14,4 |
13,2 |
11,9 |
9,4 |
5,5 |
10,6 |
7,6 |
5 |
17,2 |
1,6 |
7,7 |
15,1 |
12,9 |
11,3 |
10,6 |
3,7 |
8,6 |
5,2 |
6 |
17,6 |
2,2 |
7,0 |
15,3 |
15,7 |
9,4 |
11,4 |
7,5 |
7,0 |
4,9 |
7 |
16,2 |
2,6 |
5,1 |
16,2 |
19,0 |
10,0 |
16,2 |
6,6 |
6,3 |
4,2 |
8 |
17,0 |
4,2 |
2,8 |
16,3 |
21,4 |
10,1 |
20,2 |
9,1 |
6,3 |
3,0 |
9 |
15,6 |
6,8 |
2,7 |
16,9 |
22,3 |
8,0 |
22,3 |
8,2 |
4,8 |
4,1 |
10 |
13,4 |
11,8 |
2,2 |
16,6 |
21,8 |
7,4 |
26,7 |
11,8 |
4,5 |
2,2 |
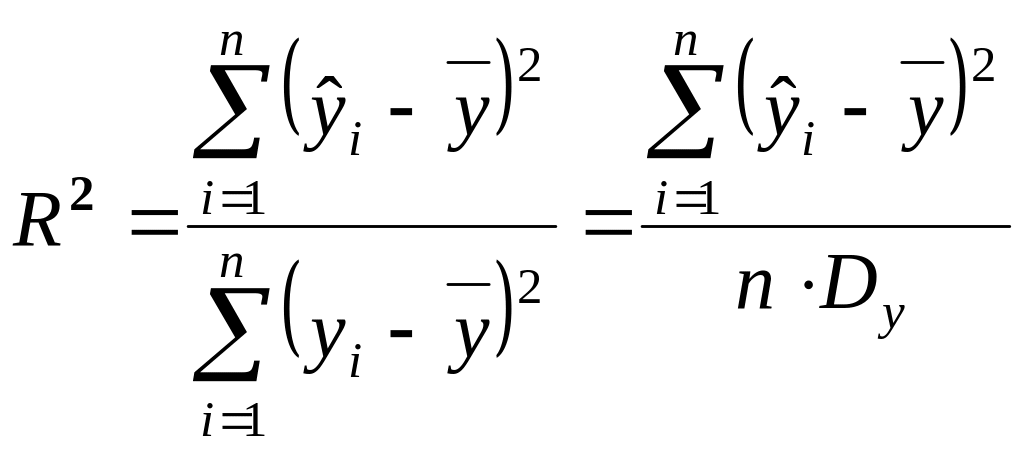