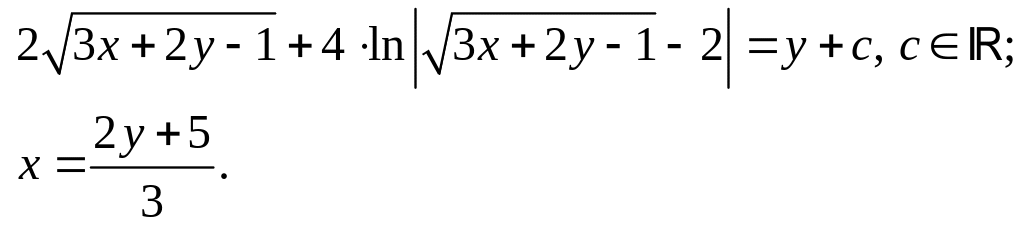Дифференциальные уравнения I порядка.

def 15 Если построение решения ДУ удаётся свести к нахождению конечного числа интегралов и производных от известных функций, а также к алгебраическим действиям, то говорят, что ДУ интегрируется в квадратурах.

def 16 Общим интегралом (общим решением) ДУ (1) при в области интегрирования ДУ (1) D, в которой выполнены условия теоремы Th1, называется однопараметрическое семейство функций

, (4)

зависящих от х, у и произвольной константы с, удовлетворяющее двум условиям:

1) при любом зафиксированном значении произвольной константы соответствующая функция , задаваемая равенством (4), является решением ДУ (2) при .

2) каково бы ни было начальное условие , решение ДУ (1) при может быть представлено в виде (4) при некотором значении произвольной постоянной .

Замечание 4 Встречается также запись ДУ первого порядка в виде суммы произведений каких-либо заданных функций переменных х и у на дифференциалы этих переменных:

(5).

ДУ вида (5) сводится к ДУ вида (1) при с помощью деления ДУ (5) на .

Дифференциальные уравнения с разделяющимися переменными.

def 17 Уравнение вида

(6)

называется дифференциальным уравнением с разделёнными переменными.

Th2 Пусть функция F(x) некоторая первообразная для функции f(x) при , и на этом интервале функция f(x) является непрерывной. Также пусть функция G(y) является некоторой первообразной при для функции g(y), и на этом интервале функция g(y) является непрерывной. Тогда общим интегралом ДУ (4) является выражение вида

, (7)

где с – произвольная константа.

Замечание 4 Формулу (5) часто записывают с использованием знака интеграла в виде:

(8)

Таким образом, чтобы решить ДУ вида (4), надо лишь проинтегрировать обе части уравнения и в одну из частей (любую) добавить константу интегрирования с.

Пример 2 Решить задачу Коши . (9)

Решение: ДУ (9) представляет собой частный случай ДУ (6). Очевидно, что область существования и интегрирования данного ДУ задаётся выражением .

Найдём неопределённые интегралы от обеих частей уравнения

(использована формула «длинного логарифма»),

(использована формула «высокого логарифма»).

Таким образом, , где . Более того, так как , то константу интегрирования можно представить в форме натурального логарифма модуля какого-либо числа . Однако в данном примере будет удобным разделить этот логарифм на 4. Указанные действия не приведут к сужению области значений для произвольной постоянной. То есть . Также, воспользовавшись свойствами логарифмов приходим к цепочке тождественных преобразований:

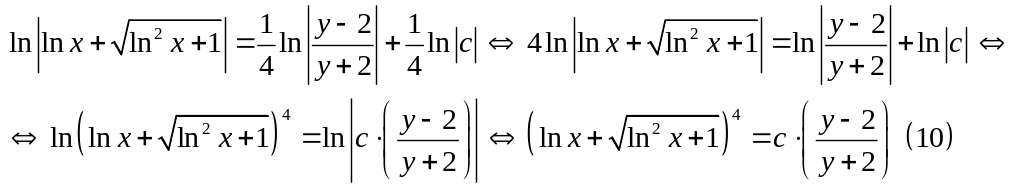
Уравнение (10) представляет собой общий интеграл ДУ (9). Теперь воспользуемся начальными условиями для выделения из общего интеграла частного интеграла, то есть задающего такое уравнение, интегральная кривая которого проходит через точку с координатами . Подставим эти значения переменных в уравнение (10) и найдём с:

Таким образом, частный интеграл (решение задачи Коши) задаётся формулой

, (11)

где - частное решение.

Заметим, что левая часть равенства (11) положительна, в то время, как правая при некоторых значениях переменной у может принимать и отрицательные значения. Если бы мы оставили в уравнении (11) знак модуля, то получили бы значение , тогда бы при снятии знака модуля всё равно пришлось бы поставить знак минус.

В данном случае выразить переменную у в явной форме можно легко и просто без особого «ущерба» (то есть одной формулой и без сужения области значений этой переменной), тем более мы привыкли принимать именно «у» за функцию, а «х» - за независимую переменную.

То есть: 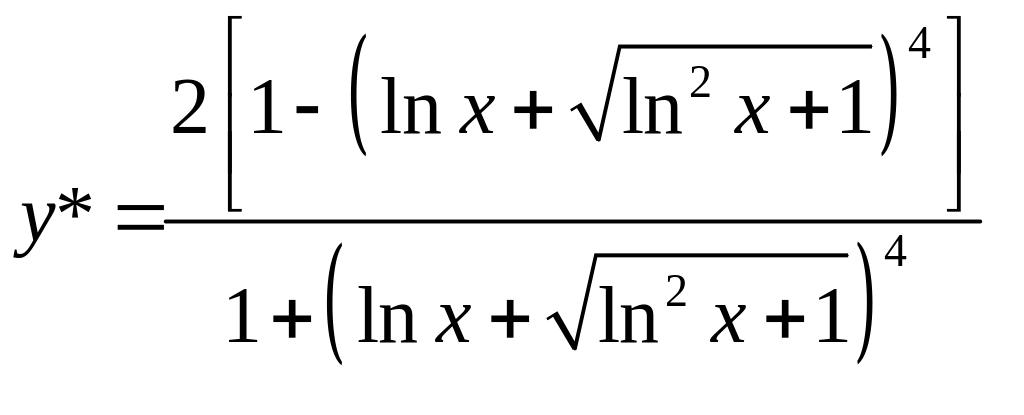. Ответ: .

def 18 Уравнения вида

(12) или (13) и т. п.

называются ДУ с разделяющимися переменными.

Очевидно, что ДУ вида (12) можно привести к уравнению вида (6), предварительно сделав замену , а затем умножив обе части ДУ (12) на . Таким образом производится процедура разделения переменных.

Аналогично можно поступить и с ДУ (13): чтобы разделить переменные надо разделить ДУ (13) на . Понятно, что и должны быть в числителе!

Таким образом, общий алгоритм решения ДУ с разделяющимися переменными:

1) Разделить переменные: С помощью операций умножения и деления привести данное ДУ с разделяющимися переменными, например вида (12) или (13), к ДУ вида (6);

2) Проинтегрировать обе части полученного ДУ с разделёнными переменными вида (6);

3) Добавить в любую часть полученного равенства произвольную константу с.

Замечание 5 В процессе разделения переменных могут быть получены как дополнительные решения, не являющиеся решениями исходного ДУ, так и потеряны решения исходного ДУ. Это может произойти в процессе умножения или деления на выражение, которое может обращаться в ноль, давая дополнительные решения при расширении области интегрирования исходного ДУ, при сужении же области интегрирования исходного ДУ, таким же образом, могут быть потеряны решения исходного ДУ. Анализ каждой такой ситуации следует проводить отдельно.

Пример 3 Решить ДУ (14)

Решение: ДУ (14) представляет собой частный случай ДУ (13). Очевидно, что область существования и интегрирования данного ДУ задаётся выражением . Выполним процедуру разделения переменных. Разделим обе части равенства (14) на выражение . Это приведёт к ДУ (15) - это ДУ с разделёнными переменными. Проинтегрируем обе части ДУ (15):

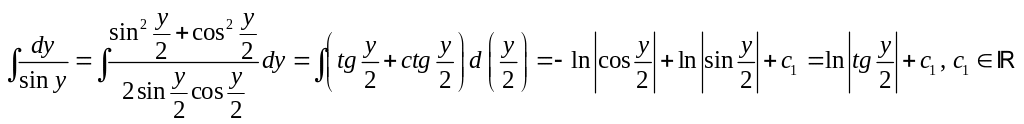
Используя полученный результат и формулу приведения, легко найти неопределённый интеграл от правой части равенства (15):

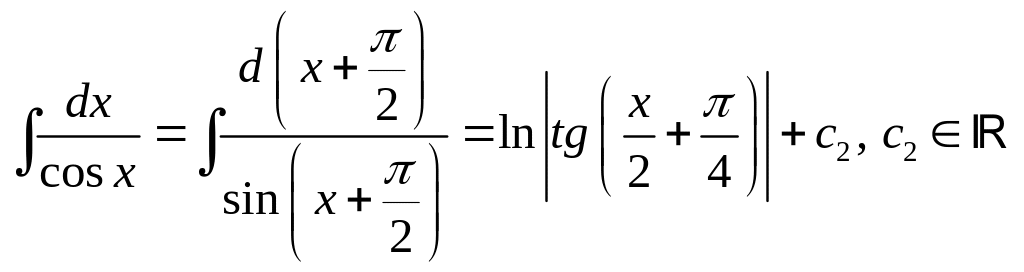
Также используя логарифмическую форму представления произвольной константы, приходим к равенству:

Используем свойства логарифмов: (16).

Таким образом, выражение (16) представляет собой общий интеграл ДУ (14).

Для того, чтобы выразить переменную у (в данном случае также несложно будет выразить и переменную х) из равенства (16) и тем самым найти общее решение ДУ (14) нужно использовать формулы тригонометрии. Это желательно делать всегда, если это возможно, так как иметь явную зависимость одной переменной через другую является более ценным по сравнению с неявным выражением. Однако, если при выражении переменной возникает необходимость к преобразованиям сужающим области значений каждой переменной, либо к переходу от одной формулы к двум и более, то это делать не рационально, так как это может привести к потере решений исходного ДУ (то которое написано изначально, дано в задании). Например, в данном случае нам необходимо воспользоваться формулами тригонометрии:

(17).

Выражение (17) представляет собой общее решение ДУ (14). При переходе от общего интеграла (16) к общему решению (17) мы не сузили области значений ни одной переменной, однако «приобрели» дополнительный параметр «п», что также является «не очень желательным». В данном примере, ответ можно записать и в явной форме (17), и в форме (16). Но запись ответа в форме (17) менее желательна.

Теперь же вспомним, что при разделении переменных (при делении на ) данные функции при определённых значения х и у могли обращаться в ноль. Проверим эти значения на их «причастность» к решению исходного ДУ (14).

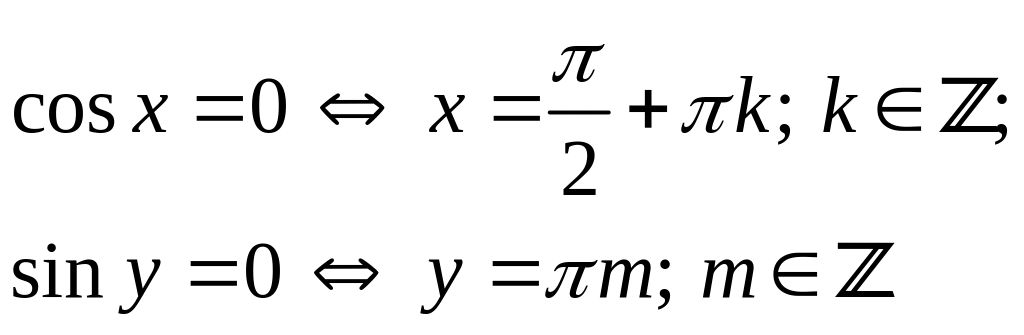(18)

Очевидно, что эти значения х и у являются решениями исходного ДУ (14). (Действительно, например, при каждом фиксированной значении параметра k, х является константой, аналогичные заключения можно сделать и для переменной у. А, как известно, дифференциал постоянной величины равен нулю.) Причём ни при одном значении произвольной постоянной с, они не попадают ни в общий интеграл (16), ни в общее решение (17) и должны быть включены в ответ. Таким образом, ответ в себя включает выражения (16) и выражения (18).

Ответ:

Дифференциальные уравнения приводящиеся к уравнениям с разделяющимися переменными.

def 19 ДУ вида

(19) или (20),

где α, β, γ, δ, k – постоянные числа, причём .

Приводится к ДУ вида (13) если произвести замену:

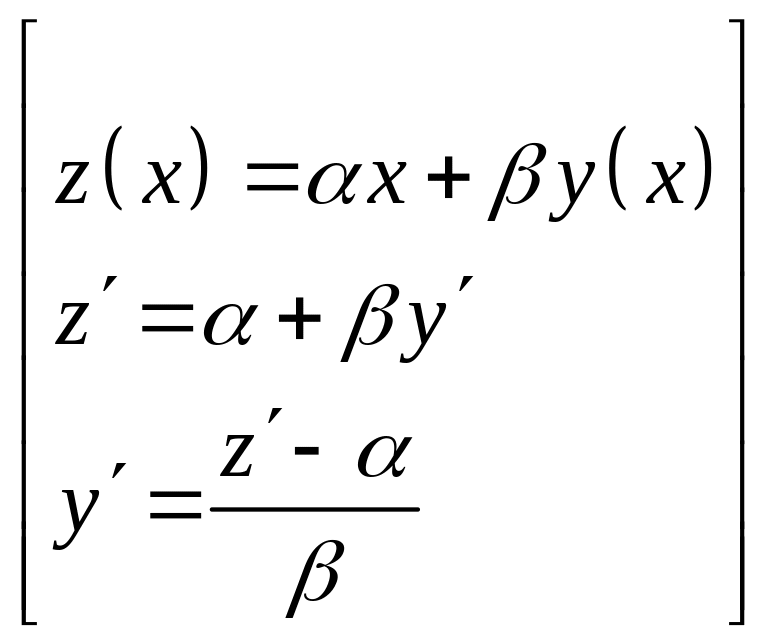(21)

Покажем, что указанная замена позволит проинтегрировать ДУ (19) как уравнение с разделяющимися переменными:

Далее, разделяя переменные в полученном равенстве, придём к уравнению вида (6), решить которое не представляет больших трудностей:

где - некоторая первообразная функции . Заметим, что при переходе от ДУ (21) к равенству интегралов, мы делили на , однако возможно, что при некоторых значениях переменной z, указанная функция, могла обращаться в ноль. При этом надо будет проанализировать этот вариант отдельно, чтобы не потерять решения. Проверка же всех полученных решений должна осуществляться только подстановкой в исходное ДУ.

Возвращаясь к исходным переменным, получим общий интеграл ДУ (20):

.

Замечание 6 В качестве новой переменной можно было взять .

Замечание 7 Иногда встречается запись ДУ в котором роли переменных поменяны: за х принимают неизвестную функцию, а за у независимую переменную. В общем это чисто семантический вопрос, ведь после получения общего интеграла и преобразование в общее решение роли этих переменных будут нивелированы. Поэтому если в ДУ встречается запись , то это полагается, что дана производная функции .

Действительно

.

В некоторых случаях целесообразно воспринимать именно х за функцию, а у за независимую переменную.

Не стоит путать: .

Пример 4 Решить ДУ (22).

Решение: ДУ (22) представляет собой частный случай ДУ (19), в котором роли переменных поменяны.

Сделаем замену:

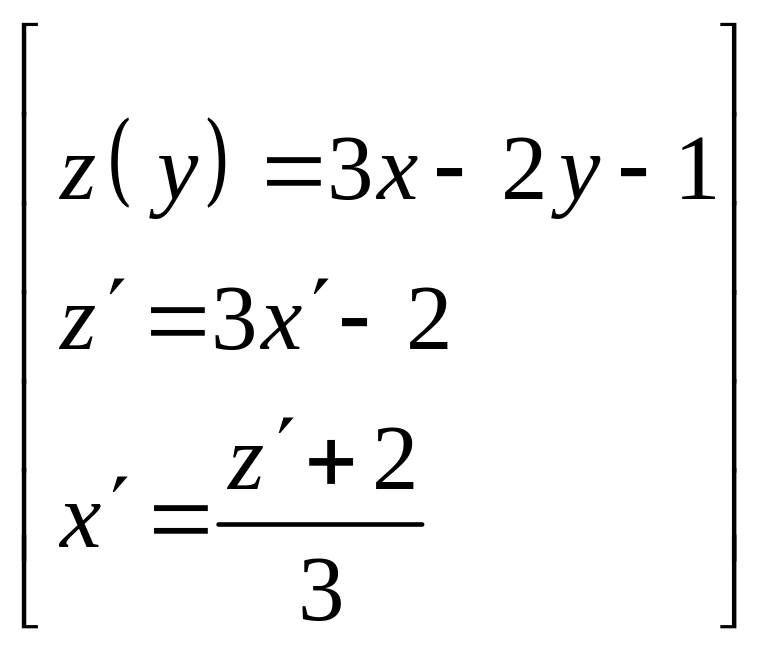(23),

Тогда получаем:

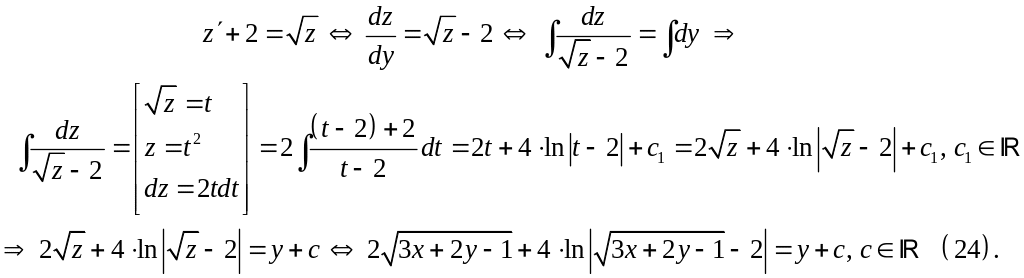
Итак, (24) представляет собой общий интеграл ДУ (22). Однако в процессе разделения переменных мы делили на (25). Проверим, не является ли решением ДУ (22), те значения переменной х, при котором нарушено условие (25):

(27)

Подставим найденные выражения (26-27) в ДУ (22):

Таким образом, надо включить частное решение (22) в ответ, так как оно не попало в общий интеграл (24) ни при одном значении произвольной константы с.

Ответ: