Лекции по гетеропереходам / курс лекций физика и технология полупроводниковых наноструктур / 16_Идеальные КТ

Тогда плотность тока излучательной рекомбинации через состояния массива КТ:

JQD = const ×∫rsp (E)ρQD (E)dE =C1 f0,

оптическое усиление:

gQD = const ×max{∫rst (E)ρQD (E)dE}=C2 (2 f0 −1)

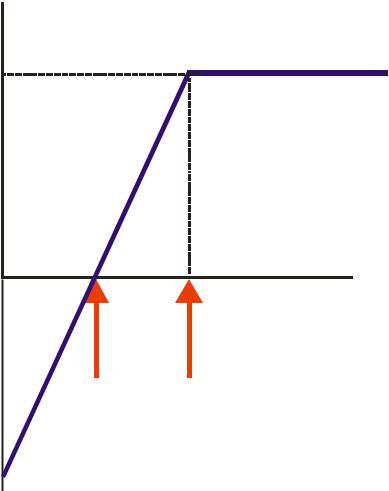
где C1(2) некоторые константы. Используя новые обозначения: J0 ≡ C1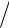2 и

≡ C2 находится искомое выражение, описывающее связь между оптическим усилением массива КТ и плотностью тока излучательной рекомбинации для идеального массива КТ:

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 11

Схематическое изображение зависимости оптического усиления от плотности тока излучательной рекомбинации для идеального массива КТ

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 12

J0 – плотность тока прозрачности, требуемого для создания инверсной заселенности массива КТ, соответствующий нулевому усилению. При этом каждая КТ массива заполнена одним экситоном.

С увеличением плотности тока растет число КТ, заполненных двумя экситонами, что приводит к линейному возрастанию усиления.

Дифференциальное усиление:

β ≡ dg dJ = g sat J0

При J=2J0 достигается максимальное заполнение состояний КТ. Все КТ массива заселены двумя экситонами и достигается максимальное возможное (насыщенное) усиление, равное gsat.

При отсутствии накачки (J=0) все состояния КТ свободны. Имеет место максимальное поглощение, равное -gsat.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 13

Плотность тока прозрачности может быть оценена из времени излучательной рекомбинации (времени жизни экситона) τ и поверхностной плотности состояний КТ, nQD:

J0 = qnQD 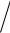τ

(q – заряд электрона)

Таким образом, в отличие от случаев объемного материала, а также квантовой ямы или квантовой проволоки, ток прозрачности идеального массива КТ не зависит от температуры, что является отражением того факта, что ширина ФПС нульмерной активной области много меньше (в идеальном случае 0) чем тепловое уширение kBT.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 14

В случае квантовой ямы

плотность тока прозрачности задается высотой ступеньки ФПС умноженной на тепловое уширение функции Ферми. ФПС практически не зависит от структурных параметров квантовой ямы, т.е. квантовая яма не может быть сконструирована таким образом, чтобы при заданной температуре обеспечить заметно меньшую плотность тока прозрачности (предел ~50А/см2).

В то же время, ФПС массива квантовых ям определяется плотностью массива, которая, вообще говоря, может быть сколь угодно малой, позволяя достичь много меньшего тока прозрачности (~5А/см2 для nQD порядка (1-5)1010 см-2)

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 15

Пороговая плотность тока идеального КТ лазера для данного уровня потерь может быть оценена из выражения для оптического усиления:

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 16

Пороговая плотность тока лазера на основе идеального массива КТ

1.Не содержит зависящих от температуры составляющих (не существует каких-либо вышележащих состояний, которые могли бы быть заселены при увеличении температуры). Следовательно, характеристическая температура T0 стремится к бесконечности.

2.В области генерации может быть весьма мала вследствие малой плотности тока прозрачности (число состояний может быть мало).

3.Стремится к бесконечности, т.е. генерация через состояния КТ невозможна), когда оптические потери превышают насыщенное усиление (т.к. число состояний ограничено).

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 17

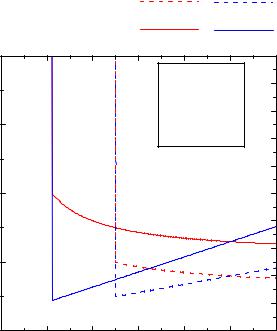
Расчет зависимости пороговой плотности тока и порогового тока при различных параметрах усиления лазера на квантовых точках

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 18

Пороговый ток линейно убывает с уменьшением длины резонатора L

Ith =W (J0 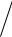g sat )[r + L(g sat +αi )

Наименьшая длина резонатора, при которой возможна генерация через состояния КТ, составляет:

Lmin = r(g sat −αi

При этом достигается наименьшее возможное значение порогового тока:

Максимальная квантовая эффективность идеального КТ лазера достигается при минимальной возможной длине резонатора:

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 19

Массив КТ с большим насыщенным усилением позволяет достичь генерации через состояния КТ в лазерах меньшей длины. Это позволяет достичь меньших значений порогового тока и более высоких значений внешней квантовой эффективности.

Можно показать, что насыщенное усиление:

∆Е – уширение ФПС массива КТ, c – скорость света в вакууме, n –

эффективный показатель преломления, M 2 - квадрат матричного элемента оптического перехода, ГQD – фактор оптического ограничения.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 16, стр. 20