§. Остаточный член формулы прямоугольников.

Вернемся, к промежутку x[–, ]. На этом промежутке, рассмотрим функцию . Функция (), обладает свойствами:

1) (– ) = – (); 2) () = f(–) + f().

Теперь вспомним: .

Разность () – S₁ это и есть, по сути, ошибка, допущенная при вычислении интеграла. Разложим () в ряд Тейлора в окрестности  = 0 с остаточным членом в интегральной форме: .

Тогда:

.

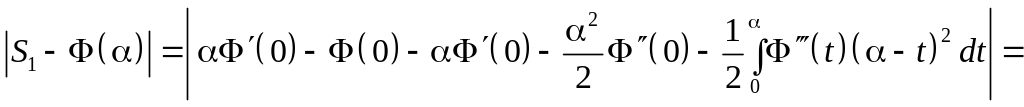
В последнем переходе мы учли, что  – нечетная функция и, следовательно  (0) = =  (0) = 0. А теперь воспользуемся теоремой о среднем и свойством 2) функции ():

.

Здесь . Кроме того, использован факт, что, взвешенное среднее находится между наибольшим и наименьшим b_i. Далее, мы предположили, что f () – непрерывная функция, хотя то же самое можно получить и при более скромных предположениях.

Оценивая ошибку на [a, b], просуммируем ошибки по всем подпромежуткам и еще раз используем теорему о взвешенных средних:

.

В итоге оценка сверху (а именно такая оценка нас и интересует) для остаточного члена формулы прямоугольников имеет вид:

.

§. Остаточные члены формул трапеций и парабол.

Без доказательства приведем оценки сверху остаточных членов формул трапеций и парабол: ; .

§. Пример применения.

Вычислить , с точностью до 10^–6.

С целью применения формулы Симпсона находим производные до четвертой включительно:

.

Чтобы исследовать поведение y⁽⁴⁾, найдем y⁽⁵⁾:

; ;

(при этом x₂  0,96; x₃  2,02).

И можно построить эскиз графика функции y⁽⁴⁾(x):

В

свете выше сказанного, целесообразно, вычисляемый интеграл представить как сумму трех интегралов: .

*) Для x[1; 2] .

На интеграл выделим 0,7 разрешенной ошибки, ибо здесь труднее всего достигнуть необходимой точности. Оценивая остаточный член формулы Симпсона, получаем:

.

Отсюда n  8.

При вычислении I₂ по формуле Симпсона надо взять n = 8.

*) Для x[2; 3] .

На интеграл выделим 0,2 разрешенной ошибки. Из условия

,

получим n  6.

При вычислении I₃ по формуле Симпсона надо взять n = 6.

*) Для x[0; 1] .

Это довольно большая величина, что делает применение формулы Симпсона нецелесообразным. Вместо этого воспользуемся разложением в ряд Маклорена:

.

В этом разложении, вследствие знакопеременности ряда имеем:

.

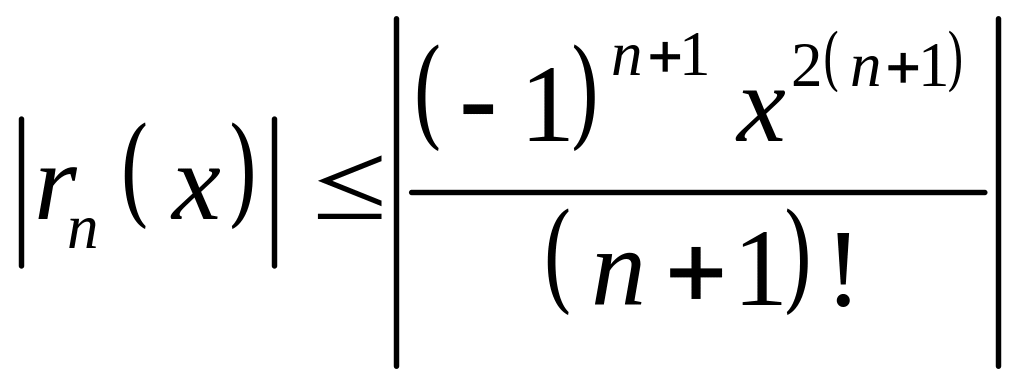Интегрирование разложения на [0; 1] дает: ,

а ошибка оценивается следующим образом:

.

Т.е. .

На интеграл осталось 0,1 допустимой ошибки

и отсюда n  9.

При вычислении I₁ с помощью разложения подынтегральной функции в ряд Маклорена достаточно взять n = 9.

Следует подумать и о том, с какой точностью вычисляются значения подынтегральной функции в точках разбиения для формулы Симпсона. Казалось бы, что, коль скоро, таких точек разбиения много, а каждые 10 слагаемых это один знак точности, то подынтегральную функцию надо вычислять со значительно большей точностью. Однако это не так, ибо в формуле Симпсона есть и деление на n, и, по сути, в точках разбиения достаточно вычислить с точностью в два раза большей, нежели вычисляемый интеграл.