§. Теоремы Гульдина.

Т. (Первая теорема Гульдина). Площадь поверхности, которую описывает кусочно-гладкая плоская кривая, вращаясь вокруг оси лежащей в той же плоскости (причем кривая не пересекает ось вращения) равна длине кривой умноженной на длину окружности, которую описывает геометрический центр масс кривой.



(рис. а) – масса кривой численно совпадает с длиной кривой при плотности , статический момент кривой равен , ордината геометрического центра масс находится по формуле 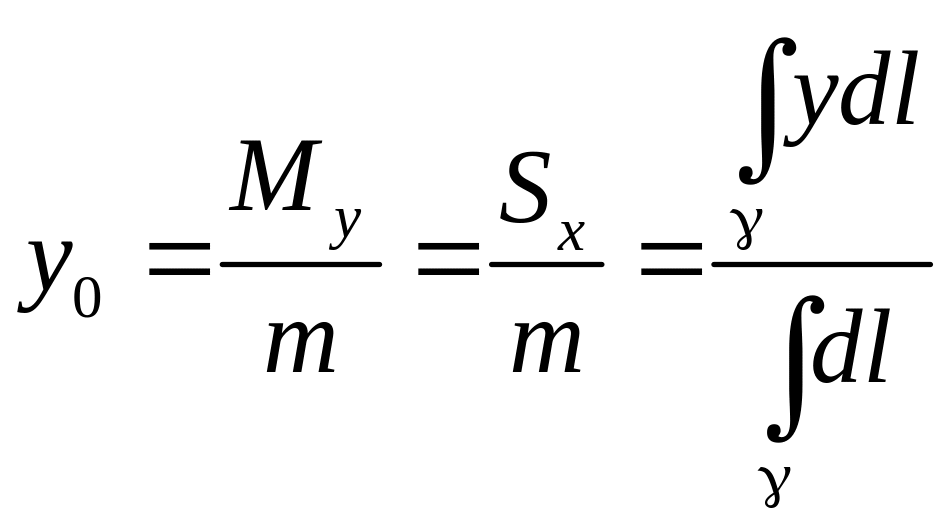. Так как кривая лежит по одну сторону от оси вращения, её ординаты все одного знака, тот же знак имеет М, то есть и, следовательно, , что и тр. док. ▲

Т. (Вторая теорема Гульдина). Объём тела, описанного плоской фигурой с кусочно-гладкой границей при вращении вокруг оси, которая лежит в одной плоскости с фигурой, по одну сторону от неё равен площади фигуры умноженной на длину окружности, которую описывает геометрический центр масс фигуры.

 (рис. б). Масса численно совпадает с площадью – , статический момент относительно оси ординат равен . Здесь – ордината геометрического центра масс элементарной полоски, которая имеет ширину и площадь . Тогда ордината центра масс равна . Поскольку ординаты всех точек фигуры положительны и положительны соответствующие моменты, получаем:

. ▲

Пример применения теорем Гульдина:

Рассмотрим тор, т.е. тело, полученное вращением круга вокруг прямой, лежащей в той же плоскости, что и круг. Причем прямая не имеет с кругом общих точек и находится на расстоянии а от центра круга радиуса , . Тогда применяя первую и вторую теоремы Гульдина, получаем: и .

Можно рассмотреть объём и площадь поверхности обобщенного тора, т.е. тела полученного вращением не окружности а, например, ромба или квадрата или каких либо других фигур.

Раздел 3. Несобственные интегралы. §. ОпределениЯ

В предыдущих разделах введено понятие определенного интеграла от ограниченной функции по ограниченному промежутку. В настоящем разделе обобщается понятие определенного интеграла на случаи, когда

*. если функция неограниченна на промежутке

*. если промежуток интегрирования – неограничен;

А. 1). Пусть функция определена в промежутке и интегрируема в любой конечной его части , так что интеграл имеет смысл при любом .

.

Def Конечный или бесконечный предел называется несобственным интегралом от функции на промежутке , и обозначается .

Аналогично определяется и несобственный интеграл .

2). Def Пусть задан конечный промежуток и функция неограниченна в окрестности точки промежутка интегрирования ( в частности, если при ). Конечный или бесконечный предел называется несобственным интегралом от неограниченной функции по промежутку и обозначается .

Аналогично определяется и несобственный интеграл .

Если рассмотренные пределы существуют, то говорят, что интегрируема в несобственном смысле, соответствующий интеграл называется несобственным и говорят, что он сходится к соответствующему пределу. Если предела не существует, то говорят, что несобственный интеграл расходится.

Б. Понятие несобственного интеграла может быть расширено и на случай, когда функция неограниченна в окрестности точек промежутка интегрирования и, кроме того, промежуток интегрирования неограничен . Как определить такой несобственный интеграл, для простоты, покажем на конкретном примере:

.

Все интегралы в правой части являются несобственными в смысле данных выше определений. Если все эти интегралы сходятся (и только в этом случае), то несобственный интеграл в левой части называется сходящимся, в противном случае – расходящимся.

В. Если функция интегрируема в собственном смысле по замкнутому промежутку, то определенный интеграл по замкнутому промежутку и несобственный интеграл по полуоткрытому промежутку совпадает.

и , причем в последнем равенстве в левой части стоит несобственный интеграл, а в правой части – интеграл Римана. В дальнейшем такое замечание, для сходящихся несобственных интегралов, становится излишним именно в связи с данным утверждением.