
- •Раздел 2. Применение определенного интеграла в геометрических и физических задачах.
- •§. Вычисление площадей плоских фигур.
- •§. Вычисление длин дуг плоских кривых.
- •§. Криволинейные интегралы I-го рода.
- •Вычисление объёмов.
- •§. Вычисление моментов и координат центра масс.
- •§. Теоремы Гульдина.
- •Раздел 3. Несобственные интегралы. §. ОпределениЯ
- •§. Основные свойства несобственного интеграла.
- •§. Критерий Коши сходимости несобственного интеграла.
- •§. Абсолютная сходимость.
- •§. ПризнакИ сравнения сходимости интегралов от знакопостоянных функций. Мажорантный признак.
- •§. Условная сходимость.
- •§. ПризнакИ Абеля и Дирихле (для функций вида ).
- •§. Поведение функции, стоящей под знаком сходящегося интеграла, на бесконечности.
- •§. Интегралы Фрулани.
- •§. Главное значение интеграла по Коши.
- •Раздел 4. Численное интегрирование §. Формулы прямоугольников, трапеций и парабол (Симпсона)
- •§. Остаточный член формулы прямоугольников.
- •§. Остаточные члены формул трапеций и парабол.
- •§. Пример применения.
- •Раздел 5. Ряды. §. Определения.
- •§. Критерий Коши сходимости ряда.
- •§. Абсолютная сходимость.
- •§. Признаки сходимости знакопостоянных рядов.
- •§. Интегральный признак Коши – Маклорена.
- •§. Признак Коши сходимости знакопостоянных рядов.
- •§. Признак дАламбера и его предельная форма.
- •§. Примеры
- •§. Признак РаАбе.
- •§. Признак Куммера.
- •§. Признаки сходимости знакопеременных рядов. А). Признак Лейбница для знакопеременных рядов.
- •Б). Признаки Абеля и Дирихле.
- •§. Несколько замечаний о перестановочности членов сходящихся – расходящихся рядов.
- •§. Функциональные ряды.
§. Несколько замечаний о перестановочности членов сходящихся – расходящихся рядов.
Если ряд сходится абсолютно, то сходится абсолютно и ряд, полученный любой перестановкой членов исходного ряда.
Т°.
Пусть дан ряд
![]() (1) с неотрицательными членами, а ряд
(1) с неотрицательными членами, а ряд
![]() (2) получается из него перестановкой
его членов. Тогда, если ряд (1) сходится,
то ряд (2) также сходится и имеет ту же
сумму.
(2) получается из него перестановкой
его членов. Тогда, если ряд (1) сходится,
то ряд (2) также сходится и имеет ту же
сумму.
∆ Пусть
ряд (1) сходится и его сумма равна S.
Рассмотрим частичную
умму ряда (2)
![]() .
Каждое из слагаемых этой суммы входит
в ряд (1). Возьмем в ряде (1) столь большое
число m первых членов,
чтобы среди них оказались все слагаемые
из
.
Каждое из слагаемых этой суммы входит
в ряд (1). Возьмем в ряде (1) столь большое
число m первых членов,
чтобы среди них оказались все слагаемые
из
![]() ,
и составим из них m-ю
частичную сумму ряда (1):
,
и составим из них m-ю
частичную сумму ряда (1):
![]() .
Так как все слагаемые
входят в
.
Так как все слагаемые
входят в
![]() ,
а остальные слагаемые
(если такие есть) неотрицательны, то
,
а остальные слагаемые
(если такие есть) неотрицательны, то
![]() .
Но частичные суммы ряда (1), ввиду не
отрицательности членов ряда, не
превосходят его суммы
.
Но частичные суммы ряда (1), ввиду не
отрицательности членов ряда, не
превосходят его суммы
![]() :
:
![]() и, следовательно,
и, следовательно,
![]() .
Так как это неравенство для любого n,
то все частичные суммы ряда (2) ограничены.
.
Так как это неравенство для любого n,
то все частичные суммы ряда (2) ограничены.
Поэтому
ряд (2) сходится и для его суммы Т
справедливо
![]() .
.
Проводя
аналогичные рассуждения не для рядов
(1) и (2), а для рядов (2) и (1) получим, что
![]() .
Из двух последних неравенств следует,
что
.
Из двух последних неравенств следует,
что
![]() ▲
▲
2) Члены условно сходящегося ряда (не абсолютно) можно переставлять так, что сумма преобразованного ряда будет равна любому, наперёд заданному элементу числовой прямой.
Изложить идею доказательства и
привести конкретный пример, например с рядом Лейбница
3) Переставить члены условно сходящегося ряда так, чтобы получился ряд сходящийся абсолютно, нельзя.
4) Если знакопостоянный ряд сходится, то он сходится абсолютно и к сумме того же знака.
5) Если ряд, у которого число членов определенного знака конечно, сходится, то он сходится абсолютно.
6)
Если у ряда число положительных
![]() и отрицательных
и отрицательных
![]() слагаемых бесконечно и он сходится
абсолютно, то ряды из
и
сходятся.
слагаемых бесконечно и он сходится
абсолютно, то ряды из
и
сходятся.
§. Функциональные ряды.
Ряд
![]() ,
у которого слагаемыми являются функции,
называется функциональным рядом.
Областью определения функционального
ряда является пересечение областей
определения отдельных его слагаемых.
,
у которого слагаемыми являются функции,
называется функциональным рядом.
Областью определения функционального
ряда является пересечение областей
определения отдельных его слагаемых.
Для
функциональных рядов рассматривается
поточечная сходимость (т.е. ряд называется
сходящимся в точке
![]() ,
если при подстановке
вместо x
получается сходящийся числовой ряд)
. Множество x,
для которых ряд сходится,
называется областью сходимости ряда.
,
если при подстановке
вместо x
получается сходящийся числовой ряд)
. Множество x,
для которых ряд сходится,
называется областью сходимости ряда.
Рассмотрим
степенной ряд
![]() .
.
Исследуем абсолютную сходимость ряда с помощью признака Коши:
![]() .
.
Для
сходимости необходимо, чтобы
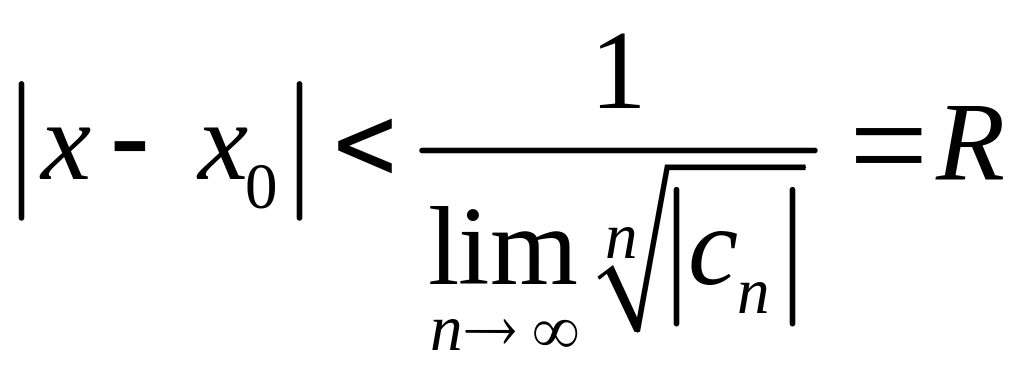 ,
т.е. степенной ряд сходится абсолютно
в круге радиуса
,
т.е. степенной ряд сходится абсолютно
в круге радиуса
 .
R –
называется радиусом сходимости степенного
ряда. Этот круг называется кругом
сходимости степенного ряда. На границе
круга сходимости ряд может, как сходиться,
так и расходиться. Абель установил, что
на границе круга сходимости (в комплексной
плоскости) существует, по крайней мере
одна точка, в которой ряд сходится
абсолютно.
.
R –
называется радиусом сходимости степенного
ряда. Этот круг называется кругом
сходимости степенного ряда. На границе
круга сходимости ряд может, как сходиться,
так и расходиться. Абель установил, что
на границе круга сходимости (в комплексной
плоскости) существует, по крайней мере
одна точка, в которой ряд сходится
абсолютно.
Вне круга сходимости ряд расходится, ибо общий член ряда не стремится к нулю.
С
помощью признака Даламбера может быть
получена еще одна формула для нахождения
радиуса сходимости степенного ряда:
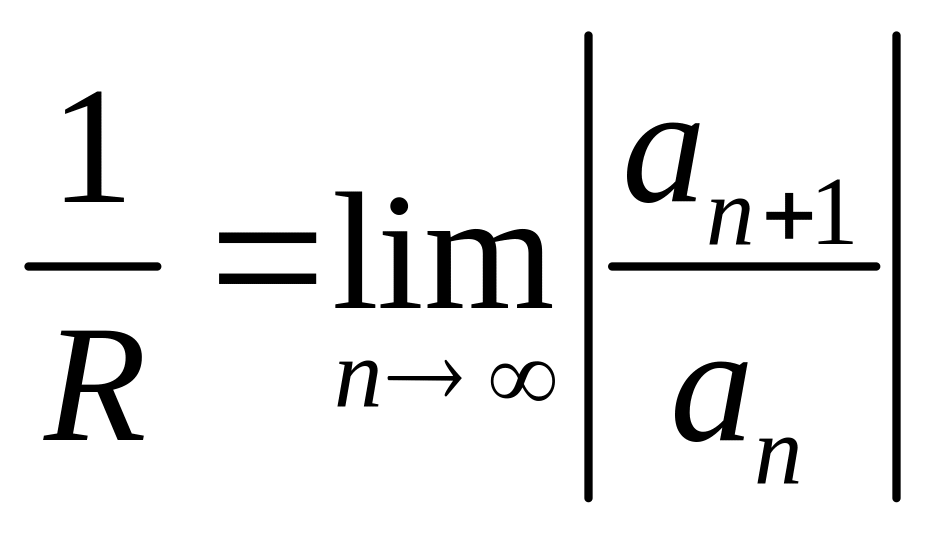 .
.
Примеры: Для следующих функциональных рядов установить области сходимости:
1.
![]() ;
2.
;
2.
 ;
;
3.
![]() ;
;
4.
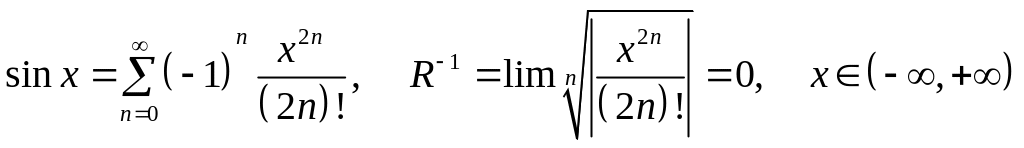 ;
;
5.
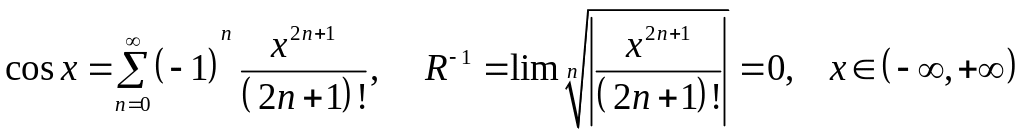 ;
;
6.
![]() .
.
