2.3. Волновая функция. Уравнение Шредингера

Квантовая механика постулирует существование некой специальной функции, с помощью которой могут быть установлены вероятные значения всех характеристик (координат, импульса, энергии и т.д.) электрона или иной микрочастицы, определяющих ее состояние. Эта функция обозначается греческой буквой  (пси) и называется волновой функцией или пси-функцией. Волновая функция не имеет простого физического смысла, однако, как было показано М. Борном, четкий физический смысл имеет ее квадрат. Величина ² в какой-либо точке пространства прямо пропорциональна вероятности нахождения (dW) частицы в бесконечно малом элементе объема (dV), включающем эту точку.

dW  ²dV

Физический смысл квадрата волновой функции налагает определенные ограничения на свойства -функции. Так, она должна быть конечна, непрерывна и однозначна. Действительно, вероятность нахождения электрона в той или иной точке всегда конечна и не может принимать несколько значений. Там, где электрон не может находиться (например, на бесконечно большом расстоянии от ядра), волновая функция должна обращаться в нуль. Волновая функция, удовлетворяющая условию

(2-5)

называется нормированной. Условие (2-4) означает, что вероятность нахождения электрона в бесконечно большом объеме равна единице, т.е., что этот электрон где-то находится. Если нормированная функция  связана с ненормированной функцией  уравнением

• = N

то коэффициент N называется нормирующим множителем.

Для выражения вероятностных значений характеристик микрочастицы через волновую функцию квантовая механика использует математический аппарат теории операторов. Оператором называется символ, показывающий, что надо сделать с данной функцией, чтобы превратить ее в некую другую функцию, т.е. оператор - это набор правил, ставящий в соответствие одной функции другую. Так, например, алгебраический оператор ln показывает, что действие его на функцию f(x) сводится к нахождению функции F(x), удовлетворяющей условию

f(x) = e^F(x)

Оператор частного дифференцирования показывает, что функцию f(x,y...) нужно дважды продифференцировать по x, полагая остальные переменные постоянными.

Квантовая механика утверждает, что каждой физической характеристике микрочастицы b соответствует определенный оператор . Так оператором координаты электрона является сама координата ( = x), импульсу электрона отвечает оператор импульса =- , где i = . Более сложным является оператор полной энергии (оператор Гамильтона или гамильтониан):

(2-6)

где m - масса электрона, U - его потенциальная энергия, ² (читается "набла квадрат") - оператор Лапласа (лапласиан)

действие которого предполагает суммирование вторых частных производных, взятых по всем координатам микрочастицы.

Чтобы найти вероятное значение того или иного свойства, нужно подействовать соответствующим оператором на -функцию, результат умножить на -функцию и проинтегрировать полученное выражение по всему объему:

(2-7)

Это утверждение имеет характер постулата, но без каких-либо исключений подтверждается опытом.

Набор волновых функций, необходимых для определения вероятностных значений свойств частицы, находят, решая для нее основное уравнение квантовой механики (Э. Шредингер, 1926). Построим уравнение Шредингера для электрона, находящегося в стационарном, то есть не изменяющемся с течением времени, состоянии, которому отвечает стоячая волна де Бройля. Для этого воспользуемся уравнением стоячей волны и принципом де Бройля.

Уравнение трехмерной стоячей волны имеет следующий вид:

(2-8)

где  - длина волны, А - амплитуда. Для электрона с учетом физического смысла волновой функции в уравнении (2-8) следует заменить A на , а вместо  подставить ее значение из уравнения де Бройля ( = h/p), что приводит к уравнению

или

Согласно (2-4)

р² =2mE_k = 2m(E - U)

где E, E_k и U - полная, кинетическая и потенциальная энергия электрона, откуда

(2-9)

Уравнение (2-9) - одна из форм уравнения Шредингера для стационарного состояния.

Перепишем уравнение (2-9) в следующей форме:

(2-10)

В соответствии с (2-5) левая часть уравнения (2-10) является результатом действия оператора полной энергии (гамильтониана) на -функцию, откуда следует наиболее общее выражение уравнения Шредингера:

(2-11)

Умножим правую и левую часть уравнения (2-11) на  и проинтегрируем по всему объему

Поскольку для стационарного состояния энергия постоянна, ее можно вынести за знак интеграла

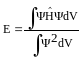(2-12)

Однако, согласно (2-5), знаменатель правой части уравнения (2-12) равен единице, соответственно

Тем самым доказана справедливость уравнения (2-7) применительно к полной энергии электрона.